Introduction
Logical Venn Diagrams, the primary point is to test the capacity of a candidate about the relation between a few things of a gathering by diagrams. In these questions, some figures of circles and some words are given. The candidate is required to pick a figure which speaks to the given words.
The article Venn Diagrams Practice Quiz 3 provides information about Venn Diagrams. The Reasoning Ability section primarily has questions with solutions are mentioned below Venn Diagrams Practice Quiz 3 sets and also useful for candidates preparing for different competitive examinations like RRB, RRB ALP/Technical Exams/Junior Engineer Recruitment Exams, SSC CGL, SSC CHSL, IBPS, SBI PO, SBI Clerks, CAT, etc.,.
Quiz
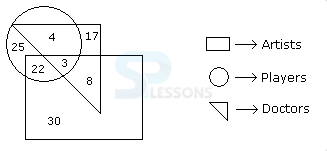
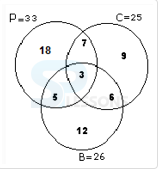
Directions (Q1 - Q5): Study the following figure and answer the questions given below.
Q1. How many doctors are neither artists nor players ?
- A. 17
B. 5
C. 10
D. 30
E. None of these
- A. 22
B. 8
C. 3
D. 30
E. None of these
- A. 5
B. 5
C. 25
D. 16
E. None of these
- A. 25
B. 17
C. 5
D. 10
E. None of these
- A. 10
B. 17
C. 30
D. 15
E. None of these
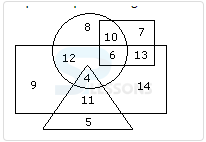
Directions (Q1 - Q4): Study the following figure and answer the questions given below.
Q1. How many educated people are employed ?
- A. 9
B. 18
C. 20
D. 15
E. None of these
- A. 9
B. 28
C. 14
D. 6
E. None of these
- A. 14
B. 5
C. 11
D. 7
E. None of these
- A. 3
B. 14
C. 22
D. 25
E. None of these
- A. 21
B. 22
C. 23
D. 24
E. None of these
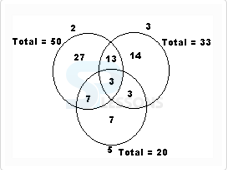
Q1. How many numbers are there between 1 and 100 that are not divisible by 2, 3 and 5 ?
From the above diagram it is clear that (27 + 14 +7 + 7 + 13 + 3 + 3 = 76 ) 76 numbers are divisible by either 2,3 or 5.
So 100 - 76 = 24 numbers are not divisible by 2,3 or 5.
Q2. In a class,7 students like to play Basketball and 8 like to play Cricket. 3 students like to play on both Basketball and Cricket. How many students like to play Basketball or Cricket or both?
From the above diagram you can clearly see that 3 students study all three subjects.
Q4. How many students study only one of the three subjects?
Number of students who study only one subject = 18 + 9 +12 = 39
Q5. In a college, 200 students are randomly selected. 140 like tea, 120 like coffee and 80 like both tea and coffee.
Number of students who like only tea = 60
Number of students who like only coffee = 40
Number of students who like neither tea nor coffee = 20
Number of students who like only one of tea or coffee = 60 + 40 = 100
Number of students who like at least one of tea or coffee = n (only Tea) + n (only coffee) + n (both Tea & coffee) = 60 + 40 + 80 = 180
- A. 21
B. 22
C. 20
D. 24
E. None of these
- A. 10
B. 9
C. 12
D. 11
E. None of these
- A. 2
B. 3
C. 5
D. 7
E. None of these
- A. 21
B. 30
C. 39
D. 42
E. None of these
- How many students like only tea?
- How many students like only coffee?
- How many students like neither tea nor coffee?
- How many students like only one of tea or coffee?
- How many students like at least one of the beverages?
- A. 150
B. 160
C. 170
D. 180
E. None of these