Description
In arithmetical reasoning, questions are based on calculations on problems, data based, ages, Venn-diagrams. This is to test the ability of candidate and the candidate is required to select the appropriate answer for the given questions.
Reasoning Ability -BANKING|SSC|RAILWAYS|INSURANCE|RECRUITMENT EXAMS – EBOOKS
Concept
Arithmetical reasoning questions are divided into four types. They are:
1. Calculations based on problems.
2. Data based questions.
3. Problems on ages.
4. Venn diagram based questions.
Model
Problems
Model 1: W, X, Y, Z play a game of cards. W says to X, "if I give you 6 cards, you will have as many as Y has and I shall have 8 less than what Y has. Also, if I take 3 cards from Y, I shall have twice as many as Z has". If X and Z together have 50 cards, how many cards has X got?
Solution:
Two hundred students appeared in an examination comprising of tests in Mathematics, Science and Social studies. The figure gives the number of students who failed in different tests. What is the percentage of candidates who failed in at least two subjects?
Solution:
Given that,
W, X, Y, Z play a game of cards.
Let
X + 6 = Y -------(i)
W - 3 = Y - 6 -------(ii)
W + 3 = 2Z -------(iii)
X + Z = 50 -------(iv)
Place Y = W + 3 from (ii) into (i)
X + 6 = W + 3
W - X = 3 -------(v)
Place Z = 50 - X from (iv) into (iii),
W + 3 = 2Z
W + 3 = 2(50 - X)
W + 3 = 100 - 2X
W + 2X = 97 -------(vi)
By solving (v) and (vi),
X = [latex]\frac{94}{3}[/latex] and W = [latex]\frac{106}{3}[/latex] = 35.3 ≅ 35
Therefore, W has approximately 35 cards.
Model 2: The data for examination is given below:
a) Students appeared - 10000.
b) Passed in three subjects only - 1500.
c) Passed in all five subjects - 5000.
d) Passed in two subjects only - 1200.
e) Passed in one subject only - 800.
f) Failed in Maths only - 200.
g) Failed in Physics only - 140
h) Failed in English only - 70.
i) Failed in Chemistry only - 150
j) failed in Biology only - 220
Answer the following questions:
1. What number of students have failed due to having failed in four or less subjects?
2. What number of students failed in all the subjects?
Solution:
1. Students failed in four or less subjects = students failed in only 1 subject + students failed in only 2 subjects + students failed in only 3 subjects + students failed in only 4 subjects
= students failed in only 1 subject + students passed in only 3 subjects + students passed in only 2 subjects + students passed in only 1 subject
= (70 + 200 + 140 + 150 + 220) + 1500 + 1200 + 800
= 4280
2. Students failed in all the subjects = students appeared - (students passed in 1, 2, 3 or 5 subjects + students failed in 1 subject only)
= 10000 - (5000 + 1500 + 1200 + 800 + 70 + 200 + 140 + 150 + 220)
= 10000 - 9280
= 720
Model 3: John is twice as old as George. Three years ago, he was three times as old as George. How old is John now?
Solution:
Let George's present age be [latex]x[/latex] years.
Then, John's present age = 2[latex]x[/latex] years.
Three years ago, George's age = ([latex]x[/latex] - 3) years.
John's age = (2[latex]x[/latex] - 3) years.
Now,
(2[latex]x[/latex] - 3) = 3([latex]x[/latex] - 3)
⇒ 2[latex]x[/latex] - 3 = 3[latex]x[/latex] - 9
⇒ [latex]x[/latex] = 6
Therefore, John's present age = 2[latex]x[/latex] = 12 years.
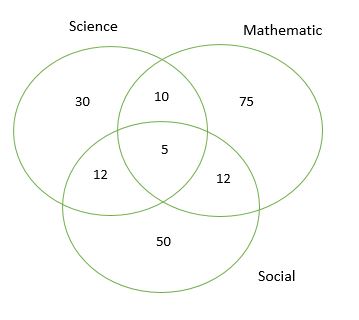
Model 4: Consider the following figure:
Number of students who failed in at least two subjects = number of candidates who failed in two or more subjects = (10 + 12 + 12 + 5) = 39
Therefore, Required percentage = ([latex]\frac{39}{500}[/latex] x 100 )% = 7.8%
Model 5: In an examination, a candidate sores 5 marks for every correct answer and loses 1 mark for every wrong answer. If the candidate attempts in all 80 questions and secures 140 marks , what is the number of questions he attempts correctly?
Solution:
Let
The number of questions attempted correctly be [latex]x[/latex]
Then, number of incorrect ones = 80 - [latex]x[/latex]
Therefore, 4[latex]x[/latex] - 1(60 - [latex]x[/latex]) = 140
⇒ 5[latex]x[/latex] = 200
⇒ [latex]x[/latex] = [latex]\frac{200}{5}[/latex]
⇒ [latex]x[/latex] = 40
Therefore, the number of questions he attempts correctly = 40.