Description
Description
The problems on dot situation includes a group of three or more geometrical figures - normally triangle, square, rectangle or/and circle having one or more dots put any time inside the bunch. This bunch is trailed by an arrangement of four option figures each made out of a group of same sort in figures.
Presently, for every dot we need to watch the region in which it is encased, i.e. to which of the geometrical figures this region is regular. At that point, we search for such a region in the four choices. When we have discovered it, we repeat the method for different dots, assuming any. The option figure which contains every single such regions is the answer.
Reasoning Ability -BANKING|SSC|RAILWAYS|INSURANCE|RECRUITMENT EXAMS – EBOOKS
 Model
Problems
Model
Problems
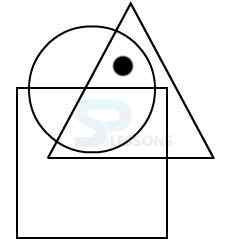
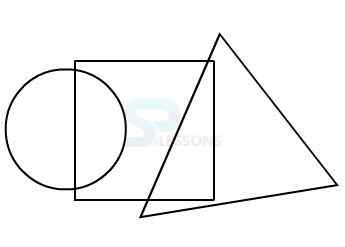
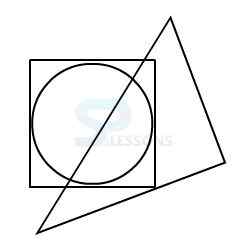
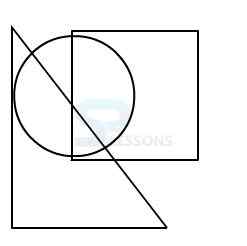
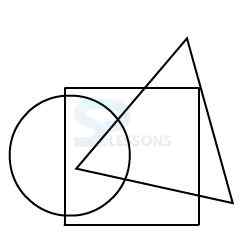
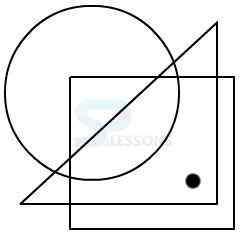
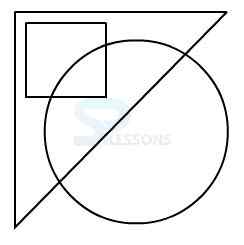
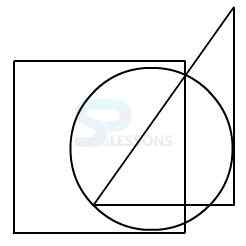
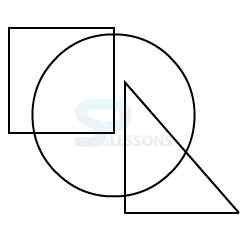
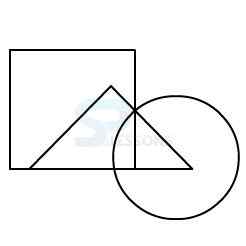
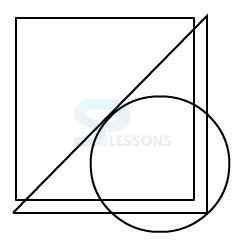
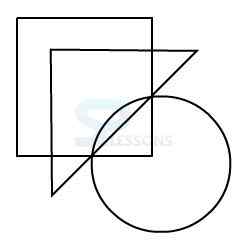
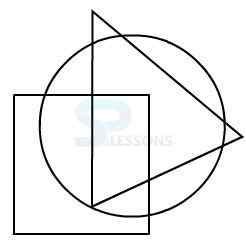
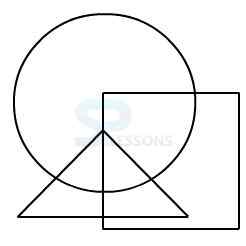
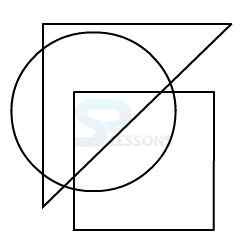
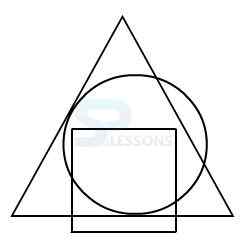
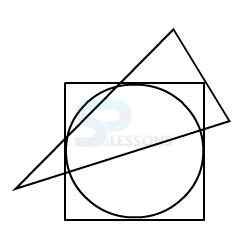
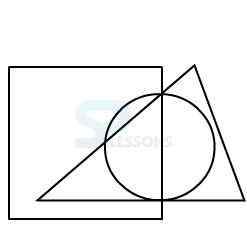
Model 1: From amongst the figures marked 1, 2, 3, and 4, select the figure which satisfies the same conditions of placement of the dot as in figure X.
X.
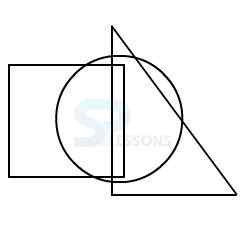
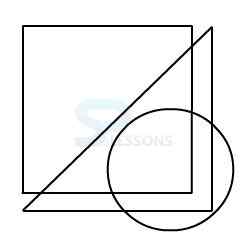
1.
2.
3.
4.
Solution:
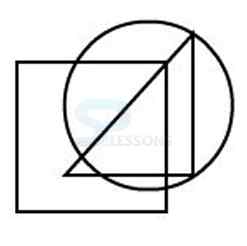
In figure X, the dot is placed in the region common to the circle and the triangle.
Amongst the four alternatives, only in figure 3, a region is common to circle and triangle only.
Therefore, figure 3 is the answer.
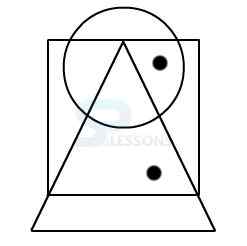
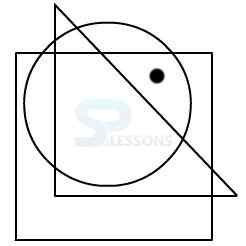
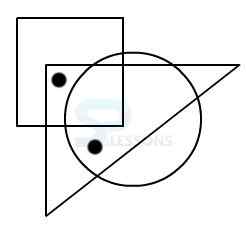
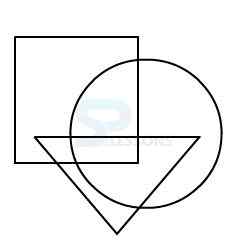
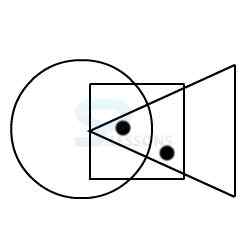
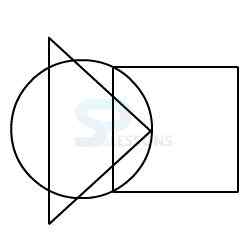
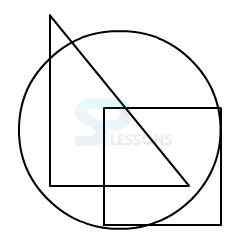
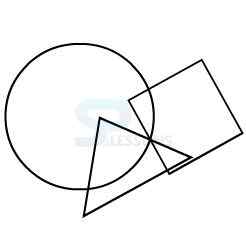
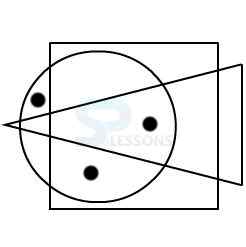
Model 2: From amongst the figures marked 1, 2, 3, and 4, select the figure which satisfies the same conditions of placement of the dot as in figure X.
X.
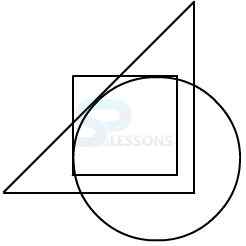
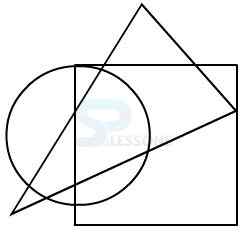
1.
2.
3.
4.
Solution:
In figure X, one of the two dots is placed in the region common to the circle and the square.
The other dot is placed in the region common to the square and the triangle.
Amongst the four alternatives, only in figure 2, there exist one region common to the square and the circle and another region common to the square and the triangle.
Therefore, figure 2 is the answer.
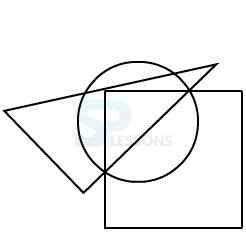
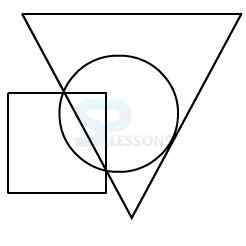
Model 3: From amongst the figures marked 1, 2, 3, and 4, select the figure which satisfies the same conditions of placement of the dot as in figure X.
X.
1.
2.
3.
4.
Solution:
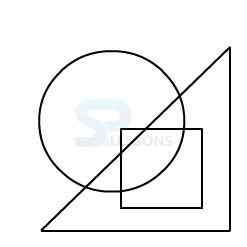
In figure X, the dot is contained in the region common to the triangle and the square only.
Out of the four alternatives, only figure 1 contains a region common to the triangle and the square only.
Therefore, figure 1 is the correct answer.
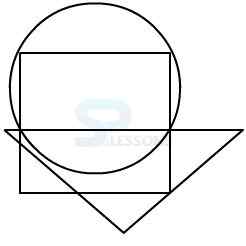
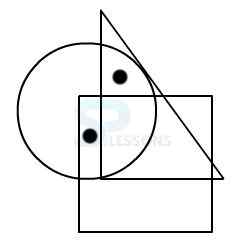
Model 4: From amongst the figures marked 1, 2, 3, and 4, select the figure which satisfies the same conditions of placement of the dot as in figure X.
X.
1.
2.
3.
4.
Solution:
In figure X, the dot is contained in the region common to the square and the circle only.
Out of four alternatives, only figure 4 contains a region common to the square and the circle only.
Therefore, figure 4 is the correct answer.
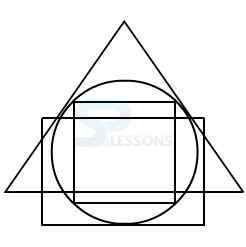
Model 5: From amongst the figures marked 1, 2, 3, and 4, select the figure which satisfies the same conditions of placement of the dot as in figure X.
X.
1.
2.
3.
4.
Solution:
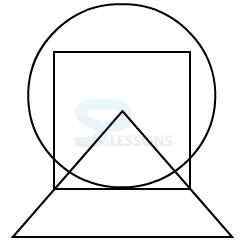
In figure X, one of the dot lies in the region common to the square and triangle and another dot lies in the region common to the circle and the triangle.
In each of the alternatives 1, 2, 3, and 4, the region common to the square and the triangle lies within the circle.
Therefore, in each of these figures, there is no region common to the square and the triangle only.
Only the alternative 3 consists of a region common to the square and the triangle only and the another region common to the circle and the triangle only.
Therefore, figure 3 is the correct answer.
Model 6: From amongst the figures marked 1, 2, 3, and 4, select the figure which satisfies the same conditions of placement of the dot as in figure X.
X.
1.
2.
3.
4.
Solution:
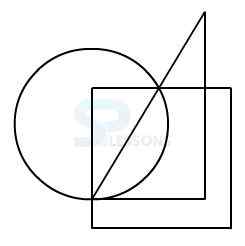
In figure X, one of the dots lies in the region common to the circle and the triangle only and the other dot lies in the region common to the circle and the square only.
In each of the figures 1, 2, 3 and 4, there is no region common to the circle and the triangle only.
Only figure 2 consists of both the types of regions.
Hence, figure 2 is correct answer.
Model 7: From amongst the figures marked 1, 2, 3, and 4, select the figure which satisfies the same conditions of placement of the dot as in figure X.
X.
1.
2.
3.
4.
Solution:
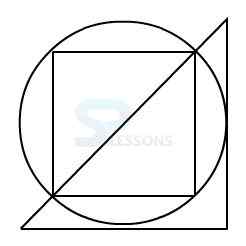
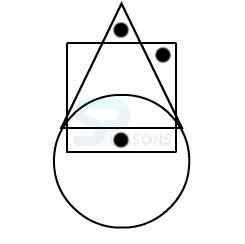
In figure X, one of the dots lies in the region common to the square and the triangle only and the other dot lies in the region common to all the three figures - the circle, the square and the triangle.
In each of the alternatives 1, and 2, there is no region common to the square and the triangle only.
In alternative 3, there is no region common to all the three figures.
Only, alternative 4 consists of both the types of regions.
Therefore, figure 4 is the correct answer.
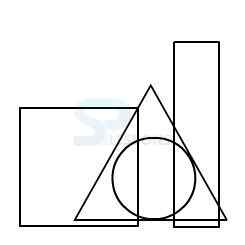
Model 8: From amongst the figures marked 1, 2, 3, and 4, select the figure which satisfies the same conditions of placement of the dot as in figure X.
X.
1.
2.
3.
4.
Solution:
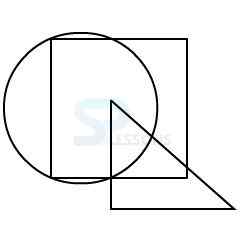
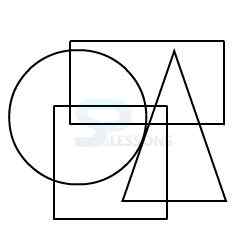
In figure X, one of the dots lies in the region common to the square and the triangle only, another dot lies in the region common to the circle and the triangle only and the third dot lies in the region common to the triangle and the rectangle only.
In figure 2, there is no region common to the square and the triangle only.
In figure 3, there is no region common to the circle and the triangle only.
In figure 4, there is no region common to the triangle and the rectangle only.
Only figure 1 consists of all the three types of regions.
Therefore, figure 1 is the correct answer.
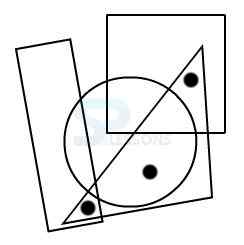
Model 9: From amongst the figures marked 1, 2, 3, and 4, select the figure which satisfies the same conditions of placement of the dot as in figure X.
X.
1.
2.
3.
4.
Solution:
In figure X, one of the dots lies in the square alone, another dot lies in the triangle alone and the third dot lies in the region common to the circle and the square.
In figure 2 there is no region that lies in the square alone.
In figure 3 there is no region that lies in the triangle alone.
In figure 4 there is no region that lies in the region common to the circle and the square only.
Only, figure 3 consists of all the three types of regions.
Hence, figure 3 is the correct answer.
Model 10: From amongst the figures marked 1, 2, 3, and 4, select the figure which satisfies the same conditions of placement of the dot as in figure X.
X.
1.
2.
3.
4.
Solution:
In figure X, one of the dots lies in the region common to the circle and the square only.
Another dot lies in the region common to all the three figures - the circle,the square and the triangle.
The third dot lies in the circle alone.
In figure 2, there is no region common to the circle and the square only and in each of the figures 3 and 4, there are regions which lie in the circle alone.
Only figure 1 consists of all the three types of regions.