Description
Description
Cubes and dices deals with the problems of the following types:-
1. Counting the number of cubes or blocks in the given figure.
2. Painting a stack of cubes.
3. Coloring the six faces of a cube.
4. Construction of boxes.
5. Problems on dice.
Reasoning Ability -BANKING|SSC|RAILWAYS|INSURANCE|RECRUITMENT EXAMS – EBOOKS
 Concept
Concept
1. Counting the number of cubes or blocks in the given figure:- When the number of cubes or blocks or cuboids in a figure are to be counted, the procedure to be adopted is described.
2. Painting a stack of cubes:- This type includes the method of solving questions based upon painting of selected sides of a stack of cubes or blocks.
3. Colouring the six faces of a cube:- Certain determinations are accommodated shading the six appearances of a cube and after that based upon these details, analyse the shading structure of the cube. Then, answer the questions based on it.
NOTE:-
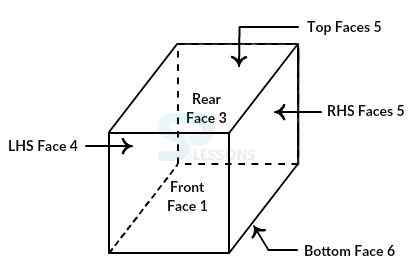
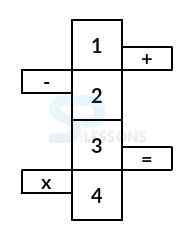
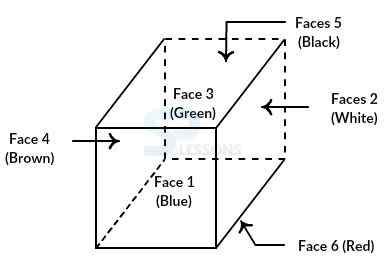
Six faces of a cube are represented as shown below:
Here,
Front face → Face no. 1,
Rear face → Face no. 3,
Top face → Face no. 5,
RHS face → Face no. 2,
LHS face → Face no. 4,
Bottom face → Face no. 6.
4. Construction of boxes:- Once in a while there are certain problems in which an applicant is given a figure including a sheet of paper cut into a particular plan and recognize the solid shape or cuboid that will be framed by folding such a sheet of paper.
On the other hand, distinguish the kind of figure that will be shaped when a specific solid shape or cuboid is unfolded. An unfolded box (cube or cuboid) may show up in any of the structures appeared in the figures given underneath. Additionally given alongside every figure, is the subtle elements of the block framed when such a sheet is folded to shape a container/box:
Type I:
In this type:
1 lies inverse 5,
2 lies inverse 4,
3 lies inverse 6.
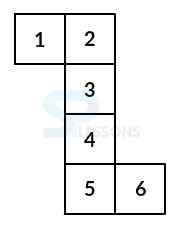
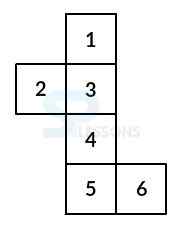
Type II:
In this type:
1 lies inverse 6,
2 lies inverse 4,
3 lies inverse 5.
Type III:
In this type:
1 lies inverse 4,
2 lies inverse 6,
3 lies inverse 5.
Type IV:
In this type:
1 lies inverse 4,
2 lies inverse 5,
3 lies inverse 6.
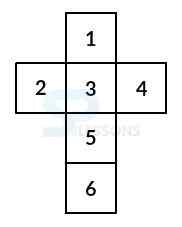
Type V:
In this type:
1 lies inverse 3,
2 lies inverse 5,
4 lies inverse 6.
Type VI:
In this type:
will be one of the faces of the cube and it lies inverse 3,
2 lies inverse 4,
1 lies inverse 5.
Type VII:
In this type:
will be one of the faces of the cube and it lies inverse 3,
2 lies inverse 4,
1 lies inverse 5.
Type VII:
In this type:
will be one of the faces of the cube and it lies inverse 3,
2 lies inverse 4,
1 lies inverse 5.
Type VIII:
In this type:
and are two faces of the cube and that lie inverse to each other,
1 lies inverse 3,
2 lies inverse 4.
5. Problems on dice:- Sometimes figures are given showing the same dice (may be in the form of a cube or a cuboid) in various positions. After observing these figures, find the number opposite a given number on the dice.  Model
Problems
Model
Problems
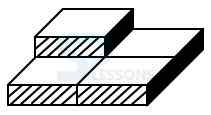
Model 1: How many blocks are there in the given figure? (S.S.C. 2002)
Solution:
From the given figure, it consists of 1 column containing 2 blocks and 3 columns containing 1 block each.
Therefore, total number of cubes = (1 x 2) + (3 x 1) = 5.
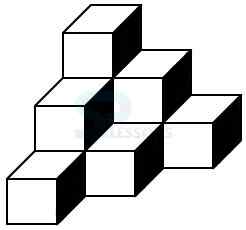
Model 2: How many cubes are there in the given figure. (Investigator's exam 2005; R.R.B. 2006)
Solution:
From the given figure, it consists of 1 column containing 3 cubes and 2 columns containing 2 cubes each and 3 columns containing 1 cubes each.
Number of cubes in columns of 3 cubes = 1 x 3 = 3.
Number of cubes in columns of 2 cubes = 2 x 2 = 4.
Number of cubes in columns of 1 cubes = 3 x 1 = 3.
Therefore, total number of cubes = 3 + 4 + 3 = 10.
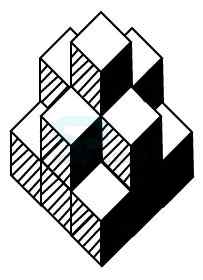
Model 3: Find the number of cubes in the given figure. (A.A.O. Exam 2003)
Solution:
From the given figure, it consists of 4 columns containing 1 cube each, 4 columns containing 2 cubes each and 1 column containing 3 cubes.
Therefore, total number of cubes = (4 x 1) + (4 x 2) + (1 x 3) = 15.
Model 4: A a symmetrical three-dimensional cube whose two adjoining faces are coloured is cut into 64 undefined minimal strong cubes. How many of these little cubes are not coloured at all? (UPSC 2005)
Solution:
Let the upper face and the RHS face of the cube be coloured as shown below:
Then, clearly the rows of smaller cubes (formed by cutting the large cube into 64 parts) which are indicated by dots, have none of their sides coloured.
Since, there are 9 such rows and each row consists of 4 cubes so there are 9 x 4 = 36 cubes which are not coloured at all.
Hence, 36 cubes are not coloured at all.
Model 5: A 3D cube, painted yellow on all sides is cut into 27 little solid cubes of equivalent size. What number of little 3D squares are painted on one single side? (R.R.B. 2004)
Solution:
The big cube can be cut into 27 small cubes as shown below:
Clearly, out of these 27 small cubes, the cubes having only one side painted are those which lie at the centre of each face of the big cube.
Since, there are 6 faces of a cube, required number of cubes is 6.
Model 6: All surfaces of a cube are coloured. If a number of smaller cubes are taken out from it, each side [latex]\frac{1}{4}[/latex] the size of the original cube's side, find the number of cubes with only one side painted. (M.B.A. 2006)
Solution:
The original (coloured) cube is divided into 64 smaller cubes as shown in the figure:
The four central cubes on each face of the larger cube, have only one side painted.
There are six faces.
Therefore, required total number of such cubes = 4 x 6 = 24.
Model 7: The six faces of a cube are coloured black, green, red, white and blue, such that (R.R.B. 2003)
(i) Red is opposite black,
(ii) Green is between red and black,
(iii) Blue is adjacent to white,
(iv) Brown is adjacent to blue,
(v) Red is at the bottom.
Based on the above given information, answer the below questions.
1. Which colour is opposite brown?
2. What are the three adjacent colours?
3. From (i) and (v), which color will be on the top of the given cube?
Solution:
From (i), it is clear that red is opposite black i.e. black is on the top i.e. on face 5.
From (iii) and (iv), it is clear that brown and white lie on either sides of blue i.e. brown is on face 4 and white on face 2.
from (v), red is at the bottom i.e. on face 6.
Then, clearly green lies on face 3. This satisfies (ii) also.
Thus the cube will be coloured as indicated in the figure below:
(1) From the figure, it is clear that white is opposite brown.
(2) Out of the three colours black, blue and white, no two colours lie on opposite faces.
Hence, these three are adjacent colours.
(3) From (v) it is clear that, red colour lies at the bottom face and from (i) it is derived that since red is opposite black.
Hence, black lies on the top.
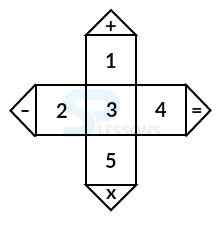
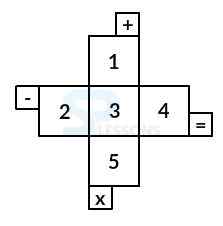
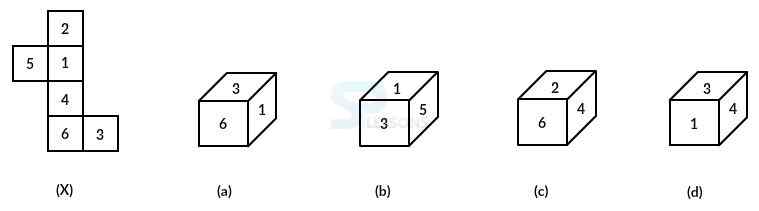
Model 8: Choose from the alternatives, the cube that can be formed by bending the piece shown in the figure (X):
Solution:
When the piece in figure X is bend to form a box then:
The number 2 will lie inverse 4,
The number 1 will lie inverse 6,
The number 5 will lie inverse 3.
Figure (a) has the numbers 1 and 6 on adjoining faces,
Figure (b) has the numbers 3 and 5 on adjoining faces,
Figure (c) has the numbers 2 and 4 on the adjoining faces.
So, these three alternatives are not possible.
Since, the numbers 1, 3 and 4 can appear on adjoining faces, so figure (d) is possible.
Therefore, only the box shown in figure (d) can be framed by bending figure X.
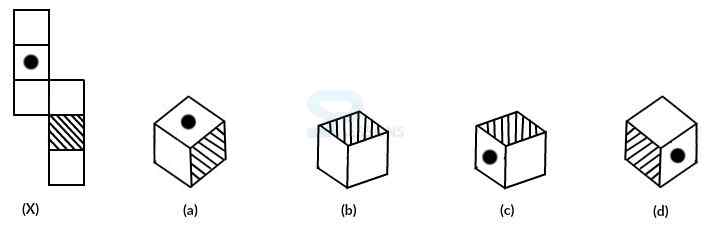
Model 9: Choose from the alternatives, the box that can be formed by bending the piece shown in figure X:
Solution:
When the piece in figure X is bend to form a box then dot and the shading must lie inverse to each other.
Hence, figures a, c and d which bear the dot and the shading on adjoining faces cannot possibly be formed by bending the piece in figure X.
Therefore, only box (b) can be formed.
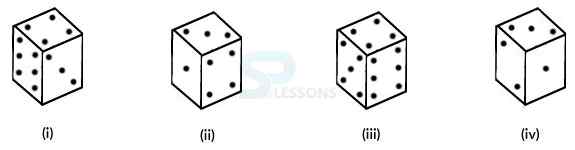
Model 10: How many dots are there on the dice face inverse the one with three dots? (S.S.C. 2002)
Solution:
From figures (i), (ii) and (iv), it is clear that 6, 4, 1 and 2 dots appear adjoining to 3 dots.
Therefor, there will be 5 dots on the face inverse the face with 3 dots.