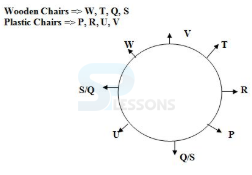
Direction(1-5): Study the following information Carefully to answer the given questions.
Eight Children P, Q, R, S, T, U, V and W are playing musical chairs. All of them are sitting on eight different chairs which are kept in a circle and face away from the centre. Four of them are wooden Chairs and four are plastic chairs.

• U sits second to the left of W and both of them sits on different types of chair. V sits second to the left of R and both sit on the same type of chair.


• T is on a wooden chair but opposite to U. Q and S are immediate neighbours of U.


• P does not sits on a wooden chair and the child who sits opposite to P does not sit on the same type of chair.


• The child who is an immediate neighbour of W and T sits on a plastic chair.

1. Who among the following sits opposite to R ?

A. R B. P C. U D. Q E. Can’t be determined

Answer - Option E
Explanation [1-5]-
2. Who among the following sits third to the right of V ?

A. P B. Q C. S D. U E. None of these

Answer - Option A
3. Which of the following children sit on the plastic chairs ?

A. QSTW B. QRTS C. PRUV D. PWUT E. None of these

Answer - Option C
4. Which of the following does not belong to the group ?

A. WV B. TR C. PV D. QU E. None of these

Answer - Option C
5. If Q is sits between W and U then who among the following sits third to the right of S ?

A. U B. P C. W D. V E. None of these

Answer - Option C

1. There is a 5 digit no. Sum of 3 pairs of digits is eleven each. Last digit is 3 times the first one. 3rd digit is 3 less than the second. 4th digit is 4 more than the second one. Find the number.

A. 25296 B. 26594 C. 24569 D. 26458 E. None of these

2. The least number which when divided by 4, 6, 8, 12 and 16 leaves a remainder of 2 in each case is

A. 46 B. 48 C. 50 D. 56 E. None of these

3. Maximum numbers that can be formed using all the 4 digits 6, 4, 8, 1 without repetition and which is divisible by 9 ?

A. 0 B. 22 C. 45 D. 567 E. 778

4. Insert the missing number. 7, 26, 63, 124, 215, 342, (....)

A. 391 B. 421 C. 481 D. 511 E. 500

5. Insert the missing number. 8, 7, 11, 12, 14, 17, 17, 22, (....)

A. 20 B. 22 C. 24 D. 27 E. 36

Answers and Explanations
1. Answer - Option A
Explanation -
We are given a 5 digit number
Let first digit be 'X'
then 5th digit is '3X'
let 2nd digit be 'Y'
then 3rd digit is 'Y - 3'
and 4th digit is 'Y + 4'
then the no is '(X)(Y)(Y - 3)(Y + 4)(3X)'
from the above we can say 3X ≤ 9
so X ≤ 3 and any of the digit in the number is ≤ 9
and also given that 3 pairs sum is 11...
Also Y – 3 ≥ 0 and Y + 4 ≤ 9
[latex]\Rightarrow[/latex] Y ≥ 3 and Y ≤ 5 i.e. Y = 3,4 or 5
for x = 1, all the conditions won’t be satisfied.
For x = 2,
Let Y = 5
∴ The number is 25296
2. Answer - Option C
Explanation -
Let’s find a number which is completely divisible by 4, 6, 8, 12 and 16.
To find such number, we need to find the LCM of all these numbers
LCM of (4,6) , 8 , 12 , 16
= 12 , 8 , 12 , 16
= LCM of (12 , 8) , LCM of (12 , 16)
= 24 , 48
= LCM of (24 , 48)
= 48
Hence 48 + 2 ie 50 will leave a remainder of 2 if divided by any of the following numbers : 4, 6, 8, 12 and 16
3. Answer - Option A
Explanation -
Since we need to use all 4 digits of the given number, we need to see that the sum of digits 6,4,8,1 = 19
And divisibility rule of 9 says that
For a number to be divisible by 9, the sum of its digits should be divisible by 9.
Hence, we can say that no numbers can be formed using all 4 digits and still divisible by 9.
4. Answer - Option D
Explanation -
Numbers are [latex]({2}^{3} - 1), ({3}^{3} - 1), ({4}^{3} - 1), ({5}^{3} - 1), ({6}^{3} - 1), ({7}^{3} - 1)[/latex] etc.
So, the next number is [latex] ({(8)}^{3} - 1) = (512 - 1) = 511.[/latex]
5. Answer - Option A
Explanation -
There are two series (8, 11, 14, 17, 20) and (7, 12, 17, 22) increasing by 3 and 5 respectively.

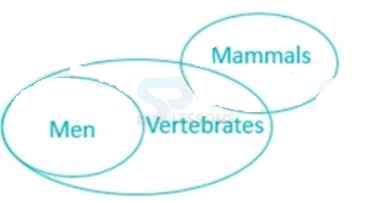
1. All men are vertebrates. Some mammals are vertebrates. Which of the following conclusions drawn from the above statement is correct?

A. All men are mammals B. All mammals are men C. Some vertebrates are mammals. D. All are correct E. None of these

2. Which of the following statements drawn from the given statements are correct? Statements: I. All watches sold in that shop are of high standard. II. Some of the HMT watches are sold in that shop. Conclusions: a) All watches of high standard were manufactured by HMT. b) Some of the HMT watches are of high standard. c) None of the HMT watches is of high standard. d) Some of the HMT watches of high standard are sold in that shop.

A. Only (a) is true B. Only (b) is true C. Only (c) is true D. Both (a) and (c) are true E. Both (b) and (d) are true

3. If MANSON is coded as 5 and BELIEVED is coded as 7, what will be coded for NEGOTIABLE?

A. 7 B. 8 C. 6 D. 10 E. 8

4. If DDMUQZM is coded as CENTRAL then UZMHKDE can be coded as.

A. VYLIJCF B. NATGLED C. TANLEDG D. TANGLED E. VYILJFC

5. In a certain code language if “TRAIN” is coded as UTDMS, then how will you code “GRASS”?

A. HTCWW B. HTDWW C. HTDXX D. HTDWX E. HTCWX

Answers and Explanations
1. Answer - Option C
Explanation -

2. Answer - Option E
3. Answer - Option B
Explanation -
As MANSON is a 6 letter word so its code is 6 – 1 = 5
Similarly BELIEVED is a 8 letter word and its code is 8 – 1 = 7
Based on the similar pattern NEGOTIABLE is a 10 letter word so its code is 10 – 1 = 9
4. Answer - Option D
Explanation -

5. Answer - Option D
Explanation -