Description
A progressive follow-up of directions and/or separation is planned and on the premise of given data it is required to determine the last direction regarding the beginning stage or the most limited separation between the beginning stage and the last point. Now and then both the last direction and the distance covered are asked.
Distance and direction sense test questions comprise of a kind of direction and/or distance riddle. Clearly, such inquiries are intended to judge the competitor's capacity to follow, take after and perceive the direction, described in somewhat complicated language, effectively.
In order to solve such questions correctly you must have the knowledge of directions on the plane of a paper. In the meantime, it is important to draw out the directions according to the data gave in the question in proper arrangement. An error at any time would change your answer decision.
Reasoning Ability -BANKING|SSC|RAILWAYS|INSURANCE|RECRUITMENT EXAMS – EBOOKS
Concept
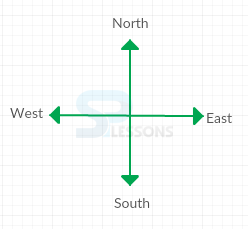
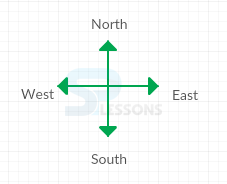
The adjoining figure shows four directions. They are East(E), West(W), North(N) and South(S).
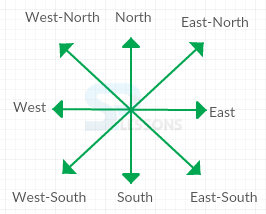
Also there are four more cardinal directions like East-North(EN), West-North(WN), East-South(ES), West-South(WS) as shown below:
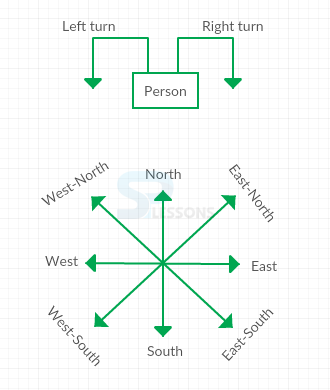
Let the person turns to all the possible directions to have a clear understanding.
Here:
1. A man facing towards North, on taking left turn will face towards West and on taking the right turn towards East.
2. A man facing towards South, on taking left turn will face towards East and on taking right turn towards West.
3. A man facing towards East, on taking left turn will face towards North and on taking right turn towards South.
4. A man facing towards West, on taking left turn will face towards South and on taking right turn towards North.
5. A man facing towards North-West, on taking left turn will face towards South-West and on taking right turn will face towards North-East.
6. A man facing towards South-West on taking left turn will face towards South-East and on taking right turn towards North-West.
7. A man facing towards South-East, on taking left turn will face towards North-East and on taking right turn towards South-West.
8. A man facing towards North-East, on taking left turn will face towards North-West and on taking right turn towards South-East.
Some important points to be noticed:
Let an example is considered, as shown below:
- If a man stands confronting/facing the east, his shadow will be towards west during the sunrise.
- The shadow of an item/object is dependably in the east during the sunset.
- In the event that a man stands confronting the North, at the time of sunrise his shadow will be towards his left and at the time of sunset it will be towards his right.
- At 12:00 twelve, the beams of the sun are vertically descending henceforth there will be no shadow.
Formulae
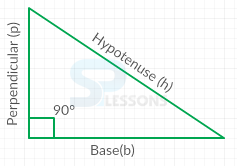
Pythagoras formula:
In order to determine the distance travelled or shortest straight distance travelled between given two points, Pythagoras formula is used. i.e.
[latex]h^2[/latex] = [latex]p^2 + b^2[/latex]
As shown, from right angled triangle
Here:
h is hypotenuse.
p is perpendicular.
b is Base.
Model
Problems
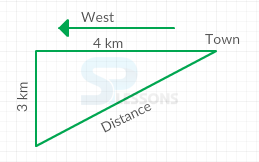
Model 1: Tom starting from his town, goes 4 km in the West, then he turns to his left and goes 3 km. What minimum distance will be covered by him to come back to his town?
Solution:
Given data:
Tom goes 4 km in the west
From there to his right, goes 3 km.
Consider the drawing shown below:
Therefore,
[latex]Distance^2[/latex] = [latex]4^2 + 3^2[/latex]
Distance = [latex]\sqrt{16 + 9}[/latex]
Distance = 5 km
Therefore, minimum distance covered by him to come back to his town = 5 km.
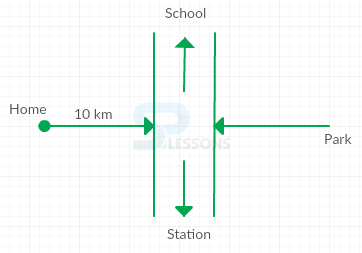
Model 2: Alice starting from home walked 10 km to reach the crossing of Museum. In which direction she was going, a road opposite to this direction goes to Park. The road to the right goes to station. If the road which goes to station is just opposite to the road which School, then in which direction to Hema is the road which goes to School?
Solution:
Given that
Alice walks 10 km and crosses Museum
Road opposite to Alice home is Park.
From there, Road to the right goes to Station.
Now, Consider the below figure:
From the figure, it is clear that
The road which goes to School is left to Alice.
Model 3: One morning after sunrise Julie while going to market met Louise at road crossing. Louise's shadow was exactly to the right of Julie. If they were face to face, which direction was Julie facing?
Solution:
Given that
Its morning. So, sun rises in the east.
Also, the shadow falls towards the west in the morning.
Now
Therefore, Louise's shadow falls to the right of the Julie. Hence Julie is facing South.
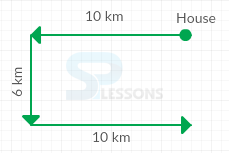
Model 4: Henry starting from his house, goes 10 km in the west, then turns to his left and goes 6 km. Finally turns to his left and goes 10 km. Now how far is Henry from his house and in what direction?
Solution:
Given that
Henry goes 10 km west.
From there, turns left and goes 6 km.
Finally to left and goes 10 km.
Now, consider the following graph:
From the figure, it is clear from third position that Henry is 6 km far from home.
Therefore, Henry is facing north direction.
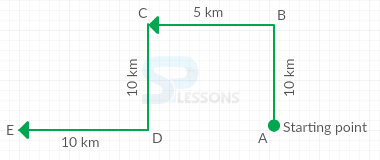
Model 5: Novel left home and cycled 10 km northwards, turned right left and cycled 5 km and turned left and cycled 10 km and turned right and cycled 10 km. How many kilometres will Novel have to cycle to reach home straight?
Solution:
Given that
Novel cycled 10 km northwards
Then turned left and cycled 5 km
then turned left and cycled 10 km and then turned right, cycled 10 km.
Consider the picture as shown below:
From figure, it is clear that
Novel starts from A, moves 10 km northwards upto B, turns left and moves 5 km upto C, turns left again and moves 10 km upto D and finally turns right and moves 10 km upto E.
Therefore,
Distance from initial position A is
AE = AD + DE
= BC + DE
= (5 + 10) km
= 15 km
Therefore, Novel have to cycle 15 km to reach home straight.