Introduction
Analytical Reasoning skills are crucial in every field that involves Numerical Reasoning, Logic, Math , Deductions & Inductions and fields where data needs to be analysed to discern patterns within the data. Analytical Reasoning is thus defined as the ability to look at the data/information and to find patterns or rules or connection between items in the information. Analytical Reasoning questions in competitive exams include both verbal & non-verbal questions and also involve a series of diagrams and pictures.
The article Analytical Reasoning Practice Quiz 2 lists different types of Analytical Reasoning questions with solutions useful for candidates preparing for different competitive examinations like RRB .RRB ALP/Technical Exams/Junior Engineer Recruitment Exams, SSC CGL,SSC CHSL, IBPS, SBI PO, SBI Clerks, CAT and etc.
Quiz
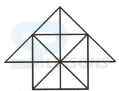
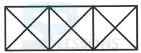
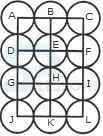
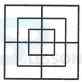
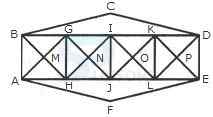
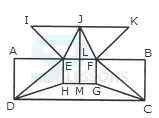
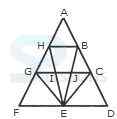
1. Count the number of triangles and squares in the given figure.
Triangles:
The simplest triangles are JBO, BKO, KDO, DFO, FGO, GHO, HIO, IJO, ABJ, BCK, CKD and DEF i.e.12 in number.
The triangles composed of two components each are IBO, BDO, DGO, GIO, ABO, CDO, CBO, CBD and DEO i.e. 9 in number.
The triangles composed of four components each are IBD, BDG, DGI, GIB, ACO and COE i.e. 6 in number.
There is only one. triangle i.e. ACE composed of eight components.
Thus, there are 12 + 9 + 6 + 1 = 28 triangles in the given figure.
Squares:
The squares composed of two components each are BKOJ, KDFO, OFGH and JOHI i.e. 4 in number.
There is only one square i.e. CDOB composed of four components.
There is only one square i.e. BDGI composed of eight components.
Thus, there are 4 + 1 + 1 = 6 squares in the given figure.
2. What is the minimum number of different colours required to paint he given figure such that no two adjacent regions have the same colour?
The regions A, C, E and G can have the same colour say colour 1.
The regions B, D, F and H can have the same colour (but different from colour 1) say colour 2.
The region 1 lies adjacent to each one of the regions A, B, C, D, E, F, G and H and therefore it should have a different colour say colour 3.
The regions J, L and N can have the same colour (different from colour 3) say colour 1.
The regions K, M and O can have the same colour (different fromthe colours 1 and 3). Thus, these regions will have colour 2.
The region P cannot have any of the colours 1 and 2 as it lies adjacent to each one of the regions J, K, L, M, N and O and so it will have colour 3.
The region Q can have any of the colours 1 or 2.
Minimum number of colours required is 3.
3. Count the number of triangles and squares in the given figure.
Triangles :
The, simplest triangles are ABI, BGI, GHI, HAI, BCJ, CFJ, FGJ, GBJ, CDK, DEK, EFK and FCK i.e. 12 in number.
The triangles composed of two components each are ABG, BGH, GHA, HAB, BCF, CFG, FGB, GBC, CDE, DEF, EFC and FGD i.e. 12 in number.
The triangles composed of four components each are AGC, BFD, HBF and GCE i.e.4 in number.
Thus, there are 12 + 12 + 4 = 28 triangles in the given figure.
Squares :
The squares composed of two components each are BJGI and CKFJ i.e. 2 in number.
The squares composed of four components each are ABGH, BCFG and CDEF i.e. 3 in number.
Total number of squares in the figure = 2 + 3 = 5.
4. Count the number of parallelogram in the given figure.
The simplest ||gms are ABFE, BCGF, CDHG, EFJI, FGKJ and GHLK. These are 6 in number.
The parallelograms composed of two components each are ACGE, BDHF, EGKI, FHLJ, ABJI, BCKJ and CDLK. Thus, there are 7 such parallelograms.
The parallelograms composed of three components each are ADHE and EHLI i.e. 2 in number.
The parallelograms composed of four components each are ACKI and BDLJ i.e. 2 in number
There is only one parallelogram composed of six components, namely ADLI.
Thus, there are 6 + 7 + 2 + 2 + 1 = 18 parallelograms in the figure.
5. In the adjoining figure, if the centres of all the circles are joined by horizontal and vertical lines, then find the number of squares that can be formed.
We shall join the centres of all the circles by horizontal and vertical lines and then label the resulting figure as shown.
The simplest squares are ABED, BCFE, DEHG, EFIH, GHKJ and HILK i.e. 6 in number.
The squares composed of four simple squares are ACIG and DFLJ i.e. 2 in number.
Thus, 6 + 2 = 8 squares will be formed.
- A. 26 triangles, 5 squares
B. 28 triangles, 5 squares
C. 26 triangles, 6 squares
D. 28 triangles, 6 squares
- A. 3
B. 4
C. 5
D. 6
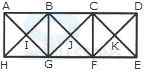
- A. 28 triangles, 3 squares
B. 24 triangles, 5 squares
C. 28 triangles, 5 squares
D. 24 triangles, 3 squares
- A. 20
B. 18
C. 16
D. 12
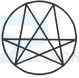
- A. 6
B. 7
C. 8
D. 1
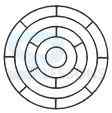
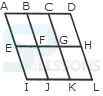
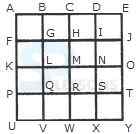
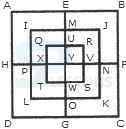
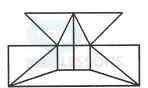
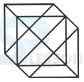
1. Count the number of squares in the given figure.
The simplest squares are ABGF, BCHG, CDIH, DEJI, FGLK, GHML, HINM, IJON, KLQP, LMRQ, MNSR, NOTS, PQVU, QRWV, RSXW and STYX i.e. 16 in number.
The squares composed of four components each are ACMK, BDNL, CEOM, FHRP, GISQ, HJTR, KMWU, LNXV and MOYW i.e. 9 in number.
The squares composed of nine components each are ADSP, BETQ, FIXU and GJYV i.e. 4 in number.
There is one square AEYU composed of sixteen components.
There are 16 + 9 + 4 + 1 = 30 squares in the given figure.
2. Find the number of quadrilaterals in the given figure.
The quadrilaterals in the figure are ABCD, ABDE, ABDF, ABDH, CDHA, CDEA, CDFA, DEAG, DEFA, FAGD and AGDH.
The number of quadrilaterals in the figure is 11.
3. Count the number of squares in the given figure.
The simplest squares are QUYX, URVY, YVSW and XYWT i.e. 4 in number.
The squares composed of two components each are IMYP, MJNY, YNKO and PYOL i.e. 4 in number.
The squares composed of three components each are AEYH, EBFY, YFCG and HYGD i.e. 4 in number.
There is only one square i.e. QRST composed of four components.
There is only one square i.e. IJKL composed of eight components.
There is only one square i.e. ABCD composed of twelve components.
Total number of squares in the given figure = 4 + 4 + 4+1 + 1 + 1 = 15.
4. What is the minimum number of colours required to fill the spaces in the given diagram without any two adjacent spaces having the same colour?
The spaces P, Q and R have to be shaded by three different colours definitely (since each of these three spaces lies adjacent to the other two).
Now, in order that no two adjacent spaces be shaded by the same colour, the spaces T, U and S must be shaded with the colours of the spaces P, Q and R respectively.
Also the spaces X, V and W must be shaded with the colours of the spaces S, T and U respectively i.e. with the colours of the spaces R, P and Q respectively. Thus, minimum three colours are required.
5. Count the number of triangles and squares in the given figure.
Triangles:
The simplest triangles are BGM, GHM, HAM, ABM, GIN, UN, JHN, HGN, IKO, KLO, LJO, JIO, KDP, DEP, ELP, LKP, BCD and AFE i.e. 18 in number.
The triangles composed of two components each are ABG, BGH, GHA, HAB, HGI, GIJ, IJH, JHG, JIK, IKL, KLJ, LJI, LKD, KDE, DEL and ELK i.e. 16 in number.
The triangles composed of four components each are BHI, GJK, ILD, AGJ, HIL and JKE i.e. 6 in number.
Total number of triangles in the figure = 18 +16 + 6 = 40.
Squares :
The squares composed of two components each are MGNH, NIOJ and OKPL i.e. 3 in number.
The squares composed of four components each are BGHA, GIJH, IKLJ and KDEL i.e. 4 in number.
Total number of squares in the figure = 3 + 4 = 7.
- A. 32
B. 30
C. 29
D. 28
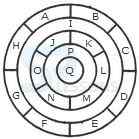
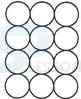
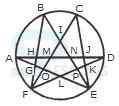
- A. 6
B. 7
C. 9
D. 11
- A. 8
B. 12
C. 15
D. 18
- A. 6
B. 5
C. 4
D. 3
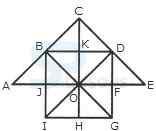
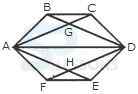
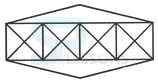
- A. 36 triangles, 7 squares
B. 38 triangles, 9 squares
C. 40 triangles, 7 squares
D. 42 triangles, 9 squares
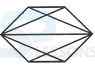
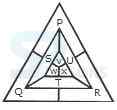
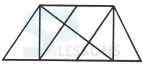
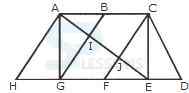
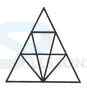
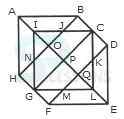
1. Find the number of triangles in the given figure.
The simplest triangles are AHG, AIG, AIB, JFE, CJE and CED i.e. 6 in number.
The triangles composed of two components each are ABG, CFE, ACJ and EGI i.e. 4 in number.
The triangles composed of three components each are ACE, AGE and CFD i.e. 3 in number.
There is only one triangle i.e. AHE composed of four components.
Therefore, There are 6 + 4 + 3 + 1 = 14 triangles in the given figure.
2. Find the minimum number of straight lines required to make the given figure.
The horizontal lines are IK, AB, HG and DC i.e. 4 in number.
The vertical lines are AD, EH, JM, FG and BC i.e. 5 in number.
The slanting lines are IE, JE, JF, KF, DE, DH, FC and GC i.e. 8 is number.
Thus, there are 4 + 5 + 8 = 17 straight lines in the figure.
3. Find the number of triangles in the given figure.
The simplest triangles are AGH, GFO, LFO, DJK, EKP, PEL and IMN i.e. 7 in number.
The triangles having two components each are GFL, KEL, AMO, NDP, BHN, CMJ, NEJ and HFM i.e. 8 in number.
The triangles having three components each are IOE, IFP, BIF and CEI i.e. 4 in number.
The triangles having four components each are ANE and DMF i.e. 2 in number.
The triangles having five components each are FCK, BGE and ADL i.e. 3 in number.
The triangles having six components each are BPF, COE, DHF and AJE i.e. 4 in number.
Total number of triangles in the figure = 7 + 8 + 4 + 2 + 3 + 4 = 28.
4. Find the number of triangles in the given figure.
The simplest triangles are AHB, GHI, BJC, GFE, GIE, IJE, CEJ and CDE i.e. 8 in number.
The triangles composed of two components each are HEG, BEC, HBE, JGE and ICE i.e. 5 in number.
The triangles composed of three components each are FHE, GCE and BED i.e. 3 in number.
There is only one triangle i.e. AGC composed of four components.
There is only one triangle i.e. AFD composed of nine components.
Thus, there are 8 + 5 + 3 + 1 + 1 = 18 triangles in the given figure.
5. Find the number of triangles in the given figure.
The simplest triangles are IJO, BCJ, CDK, KQL, MLQ, GFM, GHN and NIO i.e. 8 in number.
The triangles composed of two components each are ABO, AHO, NIJ, IGP, ICP, DEQ, FEQ, KLM, LCP and LGP i.e.10 in number.
The triangles composed of four components each are HAB, DEF, LGI, GIC, ICL and GLC i.e. 6 in number.
Total number of triangles in the figure = 8 + 10 + 6 = 24.
- A. 8
B. 10
C. 12
D. 14
- A. 16
B. 17
C. 18
D. 19
- A. 22
B. 24
C. 26
D. 28
- A. 12
B. 18
C. 22
D. 26
- A. 18
B. 20
C. 24
D. 27
Other Articles
Study Guide
Exams
| Competitive Exams - College Entrance Exams | |||
|---|---|---|---|
| Category | Notification | ||
| Diploma | NITC New Delhi | Goa Diploma Admissions 2019 | |
| Click Here For – All India Entrance Exam Notifications | |||
Daily CA
Job-Alerts
SP Quiz
| Competitive Exams - Practice Sets | |
|---|---|
| Category | Quiz |
| Quant Aptitude | Time and Work |
| Reasoning Ability | Puzzles |
| Current Affairs | Current Affairs |
GK
| General Knowledge for Competitive Examinations | |
|---|---|
| Topic | Name of the Article |
| GK - World | North America Countries Capitals Currencies |
| World Tribal Groups | |
| GK - India | Indian History Timeline – Quick Read |
| First Indians | |
| GK - Abbreviations | Finance Abbreviations |
| Computer Aptitude Abbreviations | |
| GK - Banking & Insurance | Indradhanush Strategy to Revamp PSU Banks |
| Indian Banking Structure | |
| GK - Science & Technology | Phobias List |
| Medical Science Discoveries | |
| Father of Different Fields – Science & Technology | |