Introduction
Introduction
Time and Work is one of important topic in Quantitative Aptitude Section. In Time and Work – Quiz 8 article candidates can find questions with answer. By solving this questions candidates can improve and maintain, speed, and accuracy in the exams. Time and Work – Quiz 8 questions are very useful for different exams such as IBPS PO, Clerk, SSC CGL, SBI PO, NIACL Assistant, NICL AO, IBPS SO, RRB, Railways, Civil Services etc.
 Q1
Q1
(x - 2) men can do a piece of work in x days and (x + 7) men can do 75% of the same work in (x - 10)days. Then in how many days can (x + 10) men finish the work?
- A. 11 days
B. 12 days
C. 13 days
D. 14 days
[latex]\frac {3}{4}[/latex] × (x − 2) x = (x + 7)(x − 10)
⇒[latex]{x}^{2}[/latex] − 6x − 280 = 0
⇒ x = 20 and x =-14
so, the acceptable values is x = 20
Therefore, Total work = (x - 2)x = 18 x 20 = 360 unit
Now 360 = 30 x k
⇒ k = 12 days
 Q2
Q2
A is twice as good a workman as B and is therefore able to finish a piece of work in 30 days less than B.In how many days they can complee the whole work; working together?
- A. 20 days
B. 30 days
C. 40 days
D. 10 days
Ratio of times taken by A and B = 1 : 2.
The time difference is (2 - 1) 1 day while B take 2 days and A takes 1 day.
If difference of time is 1 day, B takes 2 days.
If difference of time is 30 days, B takes 2 x 30 = 60 days.
So, A takes 30 days to do the work.
A's 1 day's work = [latex]\frac {1}{30}[/latex]
B's 1 day's work = [latex]\frac {1}{60}[/latex]
(A + B)'s 1 day's work = [latex]\frac {1}{30} + \frac {1}{60} = \frac {1}{120}[/latex]
A and B together can do the work in 20 days.
 Q3
Q3
A works twice as fast as B. If B can complete a work in 18 days independently,the number of days in which A and B can together finish the work is:
- A. 4 days
B. 6 days
C. 8 days
D. 10 days
Ratio of rates of working of A and B = 2 : 1. So, ratio of times taken = 1:2
Therefore, A's 1 day's work = [latex]\frac {1}{9}[/latex]
B's 1 day's work = [latex]\frac {1}{18}[/latex]
(A+B)'s 1 day's work= [latex]\frac {1}{9} + \frac {1}{18} = \frac {1}{6}[/latex]
so, A and B together can finish the work in 6 days
 Q4
Q4
A can do a certain work in the same time in which B and C together can do it.If A and B together could do it in 20 days and C alone in 60 days ,then B alone could do it in:
- A. 20 days
B. 40 days
C. 50 days
D. 60 days
(A + B)'s 1 day's work = [latex]\frac {1}{30}[/latex]
C's 1 day work = [latex]\frac {1}{60}[/latex]
(A + B + C)'s 1 day's work = [latex]\frac {1}{20} + \frac {1}{60} = \frac {1}{15}[/latex]
Also A's 1 day's work = (B + C)'s 1 day's work
Therefore, we get: 2 x (A's 1 day 's work) = [latex] \frac {1}{15}[/latex]
[latex] \Rightarrow[/latex] A's 1 day's work = [latex] \frac {1}{30}[/latex]
Therefore, B's 1 day's work = [latex]\frac {1}{20} - \frac {1}{30} = \frac {1}{60}[/latex]
So, B alone could do the work in 60 days.
 Q5
Q5
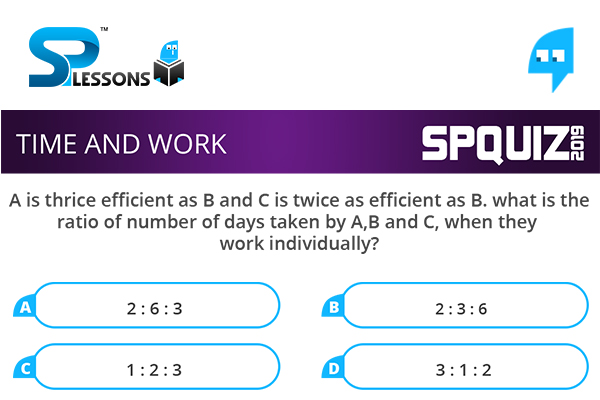
A is thrice efficient as B and C is twice as efficient as B. what is the ratio of number of days taken by A,B and C, when they work individually?
- A. 2 : 6 : 3
B. 2 : 3 : 6
C. 1 : 2 : 3
D. 3 : 1 : 2
Ratio of efficiency A : B : C
Ratio of efficiency 3 : 1 : 2
Ratio of No.of days [latex]\frac {1}{3}[/latex] : [latex]\frac {1}{1}[/latex] : [latex]\frac {1}{2}[/latex]
or 2 : 6 :3
Hence A is correct.
 Study Guide
Study Guide
| Section Name | Name of the Article |
|---|---|
| Study-Guide | Quantitative Aptitude |
Reasoning Ability |
|
General Awareness |
|
Computer Awareness |
|
English Knowledge |
|
World of Words (WOW) |
|
Descriptive Test |
 Exams
Exams
| Category | Notification |
|---|---|
| Degree & PG | NPAT 2019 |
| Engineering | HPCET 2019 |
| UPJEE 2019 | |
| AUEET 2019 | |
| VITMEE | |
| Teaching | TS SET 2019 |
| Medical | FMGE 2019 |
 CA
CA
 SP Quiz
SP Quiz
| Category | Quiz |
|---|---|
| Quant Aptitude | |
| Permutation and Combination | |
| Speed and Time | |
| Mensuration | |
| Profit and Loss | |
| Reasoning Ability | Puzzles |
| Seating Arrangement | |
| Direction Sense | |
| General Awareness | General Awareness Quiz |
| Banking Awareness | Banking Awareness Quiz |
| Computer Awareness | Computer Awareness Quiz |