Introduction
Introduction
Mensuration is one of important topic in Quantitative Aptitude Section. In Mensuration – Quiz 8 article candidates can find questions with answer. By solving this questions candidates can improve and maintain, speed, and accuracy in the exams. Mensuration – Quiz 8 questions are very useful for different exams such as IBPS PO, Clerk, SSC CGL, SBI PO, NIACL Assistant, NICL AO, IBPS SO, RRB, Railways, Civil Services etc.
 Q1
Q1
A cone and sphere have the same radius of 12 cm. Find the height of the cone if the cone and sphere have the same volume.
- A. 18 cm
B. 24 cm
C. 36 cm
D. 48 cm
Let the height of the cone be h [latex]\frac {}{}[/latex]
Volume of the cone
= [latex]\frac {1}{3} \times \pi \times {(12)}^{2} \times h[/latex]
= 48πh [latex]{cm}^{3}[/latex]
Volume of the sphere
= [latex]\frac {4}{3} \times \pi \times {(r)}^{3}[/latex]
= [latex]\frac {4}{3} \times \pi \times {(12)}^{3}[/latex]
= 2304 [latex]{cm}^{3}[/latex]
Since the volumes are equal
48πh = 2304π
Solving for h
h = [latex]\frac {2304π}{48π}[/latex]
= 48 cm
 Q2
Q2
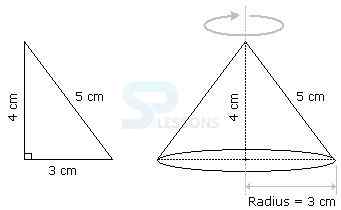
A right triangle with sides 3 cm, 4 cm and 5 cm is rotated the side of 3 cm to form a cone. The volume of the cone so formed is:
- A. 12π [latex]{cm}^{3}[/latex]
B. 15π [latex]{cm}^{3}[/latex]
C. 16π [latex]{cm}^{3}[/latex]
D. 20π [latex]{cm}^{3}[/latex]
 Q3
Q3
In a shower, 5 cm of rain falls. The volume of water that falls on 1.5 hectares of ground is:
- A. 75 cu. m
B. 750 cu. m
C. 7500 cu. m
D. 75000 cu. m
1 hectare = 10,000 [latex]{m}^{2}[/latex]
So, Area = (1.5 x 10000) [latex]{m}^{2}[/latex] = 15000 [latex]{m}^{2}[/latex].
Depth = [latex]\frac {5}{100} m = \frac {1}{20}m[/latex]
Volume = (Area x Depth) = [latex](15000 \times \frac {1}{20}) {m}^{3} = 750 {m}^{3} [/latex]
 Q4
Q4
A hall is 15 m long and 12 m broad. If the sum of the areas of the floor and the ceiling is equal to the sum of the areas of four walls, the volume of the hall is:
- A. 720
B. 900
C. 1200
D. 1800
2(15 + 12) x h = 2(15 x 12)
[latex]\Rightarrow h = \frac {180}{27} m = \frac {20}{3} m [/latex]
i.e,Volume = [latex](15 \times 12 \times \frac {20}{3}){m}^{3} = 1200 {m}^{3}[/latex]
 Q5
Q5
A hollow iron pipe is 21 cm long and its external diameter is 8 cm. If the thickness of the pipe is 1 cm and iron weighs 8 g/[latex]{cm}^{3}[/latex], then the weight of the pipe is:
- A. 3.6 kg
B. 3.696 kg
C. 36 kg
D. 36.9 kg
External radius = 4 cm,
Internal radius = 3 cm.
Volume of iron = [latex](\frac {22}{7} \times [{(4)}^{2}) - {(3)}^{2}]\times 21) {cm}^{3}[/latex]
= [latex](\frac {22}{7} \times 7 \times 1 \times 21) {cm}^{3}[/latex]
= 462 [latex]{cm}^{3}[/latex]
 Study Guide
Study Guide
| Section Name | Name of the Article |
|---|---|
| Study-Guide | Quantitative Aptitude |
Reasoning Ability |
|
General Awareness |
|
Computer Awareness |
|
English Knowledge |
|
World of Words (WOW) |
|
Descriptive Test |
 Exams
Exams
| Category | Notification |
|---|---|
| Graduate | NPAT 2019 |
| Engineering | AIEEA PG 2019 |
| AIEEA UG 2019 | |
| AUEET 2019 | |
| VITMEE | |
| Teaching | TS SET 2019 |
| Medical | FMGE 2019 |
 CA
CA
 SP Quiz
SP Quiz
| Category | Quiz |
|---|---|
| Quant Aptitude | |
| Permutation and Combination | |
| Speed and Time | |
| Mensuration | |
| Profit and Loss | |
| Reasoning Ability | Puzzles |
| Seating Arrangement | |
| Direction Sense | |
| General Awareness | General Awareness Quiz |
| Banking Awareness | Banking Awareness Quiz |
| Computer Awareness | Computer Awareness Quiz |