Introduction
Introduction
Speed and Time is one of important topic in Quantitative Aptitude Section. In Speed and Time – Quiz 4 article candidates can find questions with an answer. By solving this questions candidates can improve and maintain, speed, and accuracy in the exams. Speed and Time – Quiz 4 questions are very useful for different exams such as IBPS PO, Clerk, SSC CGL, SBI PO, NIACL Assistant, NICL AO, IBPS SO, RRB, Railways, Civil Services etc.
 Q1
Q1
A man whose speed is 4.5 kmph in still water rows to a certain upstream point and back to the starting point in a river which flows at 1.5 kmph, find his average speed for the total journey ?
- A. 5 kmph
B. 7 kmph
C. 3 kmph
D. 4 kmph
Speed of Man = 4.5 kmph
Speed of stream = 1.5 kmph
Speed in DownStream = 6 kmph
Speed in UpStream = 3 kmph
Average Speed = [latex]\frac {(2 x 6 x 3)}{9}[/latex] = 4 kmph.
 Q2
Q2
A man in a train notices that he can count 41 telephone posts in one minute. If they are known to be 50 metres apart, then at what speed is the train travelling?
- A. 60 km/hr
B. 100 km/hr
C. 110 km/hr
D. 120 km/hr
Number of gaps between 41 poles = 40
So total distance between 41 poles = 40 [latex]\times[/latex] 50
= 2000 meter = 2 km
In 1 minute train is moving 2 km/minute.
Speed in hour = 2 [latex]\times[/latex] 60 = 120 km/hour
 Q3
Q3
A man covered a certain distance at some speed. Had he moved 3 kmph faster, he would have taken 40 minutes less. If he had moved 2 kmph slower, he would have taken 40 minutes more. The distance (in km) is
- A. 30
B. 36
C. 40
D. 42
Let distance = x km and usual rate = y kmph.
Then, [latex]\frac {X}{Y}[/latex] - [latex]\frac {X}{(y+3)}[/latex] = [latex]\frac {40}{60} \rightarrow[/latex] 2y (y+3) = 9x ----- (i)
Also, [latex]\frac {X}{(Y - 2)}[/latex] - [latex]\frac {X}{Y}[/latex] = [latex]\frac {40}{60} \rightarrow[/latex] y(y-2) = 3x -------- (ii)
On dividing (i) by (ii), we get:
x = 40 km.
 Q4
Q4
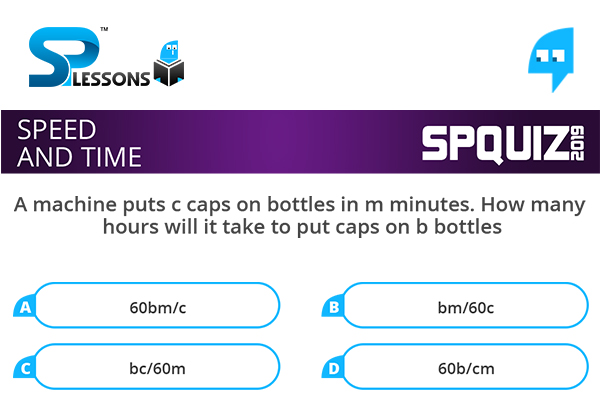
A machine puts c caps on bottles in m minutes. How many hours will it take to put caps on b bottles
- A. 60bm/c
B. bm/60c
C. bc/60m
D. 60b/cm
Substitute sensible numbers and work out the problem. Then change the numbers back to letters. For example if the machine puts 6 caps on bottles in 2 minutes, it will put [latex]\frac {6}{2}[/latex] caps on per minute, or ([latex]\frac {6}{2}[/latex]) x 60 caps per hour. Putting letters back this is 60c/m.If you divide the required number of caps (b) by the caps per hour you will get time taken in hours. This gives bm/60c
 Q5
Q5
P is faster than Q. P and Q each walk 24 km. The sum of their speeds is 7 km/hr and the sum of times taken by them is 14 hours. Then, P's speed is equal to ?
- A. 3 km/hr
B. 4 km/hr
C. 5 km/hr
D. 6 km/hr
Let P's speed = x km/hr.
Then, Q's speed = (7 - x) km/ hr.
So, [latex]\frac{24}{x}[/latex] + [latex]\frac{24}{(7 - x)}[/latex] = 14
[latex]{x}^{2}[/latex] - 98x + 168 = 0
(x - 3)(x - 4) = 0 => x = 3 or 4.
Since, P is faster than Q,
so P's speed = 4 km/hr and Q's speed = 3 km/hr.