Introduction
Introduction
Quadratic Equation is one of important topic in Quantitative Aptitude Section. In Quadratic Equation - Quiz 1 article candidates can find a question with an answer. By solving this question candidates can improve and maintain, speed, and accuracy in the exams. The Quadratic Equation - Quiz 1 questions are very useful for different exams such as IBPS PO, Clerk, SSC CGL, SBI PO, NIACL Assistant, NICL AO, IBPS SO, RRB, Railways, Civil Services etc.
 Q1
Q1
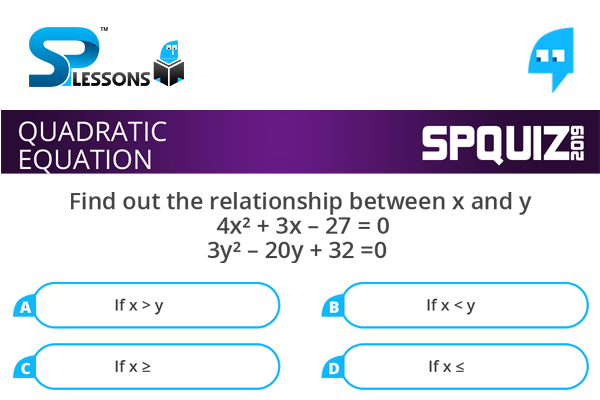
Directions: In the following questions, two equations numbered are given in variables x and y. You have to solve both the equations and find out the relationship between x and y. Then give answer accordingly-
Find out the relationship between x and y.
- [latex]4{x}^{2} + 3x - 27 = 0[/latex]
[latex]3{y}^{2} - 20y + 32 = 0[/latex]
- A. If x > y
B. If x < y
C. If x [latex]\geq[/latex]
D. If x [latex]\leq[/latex]
x =2.25, -3
y = [latex]\frac {8}{3}[/latex], 4
Put all values on number line and analyze the relationship
-3……..2.25……..[latex]\frac {8}{3}[/latex]……….4
 Q2
Q2
Find the roots of the quadratic equation: [latex]{x}^{2}[/latex] + 2x - 15 = 0?
- A. -5, 3
B. 3, 5
C. -3, 5
D. -3, -5
[latex]{x}^{2}[/latex] + 2x - 15 = 0
x(x + 5) - 3(x + 5) = 0
(x - 3)(x + 5) = 0
x = 3 or x = -5.
 Q3
Q3
The roots of the equation [latex]3{x}^{2}[/latex] - 12x + 10 = 0 are?
- A. rational and unequal
B. complex
C. real and equal
D. irrational and unequal
The discriminant of the quadratic equation is [latex]{(-12)}^{2}[/latex] - 4(3)(10) i.e., 24. As this is positive but not a perfect square, the roots are irrational and unequal.
 Q4
Q4
If alpha and beta are the roots of the equation x² – 9x + 14 = 0 then find the value of [latex]{A}^{2}[/latex] + [latex]{B}^{2}[/latex].
- A. 25
B. 28
C. 53
D. 81
 Q5
Q5
If the roots of a quadratic equation are 20 and -7, then find the equation?
- A. [latex]{x}^{2} + 13x - 140 = 0[/latex]
B. [latex]{x}^{2} - 13x + 140 = 0[/latex]
C. [latex]{x}^{2} - 13x - 140 = 0[/latex]
D. [latex]{x}^{2} + 13x + 140 = 0[/latex]
Any quadratic equation is of the form
[latex]{x}^{2}[/latex] - (sum of the roots)x + (product of the roots) = 0 ---- (1)
where x is a real variable. As sum of the roots is 13 and product of the roots is -140, the quadratic equation with roots as 20 and -7 is: [latex]{x}^{2}[/latex] - 13x - 140 = 0.