Introduction
Introduction
Probability is one of important topic in Quantitative Aptitude Section. In Probability – Quiz 5 article candidates can find questions with answer. By solving this questions candidates can improve and maintain, speed, and accuracy in the exams. Probability - Quiz 5 questions are very useful for different exams such as IBPS PO, Clerk, SSC CGL, SBI PO, NIACL Assistant, NICL AO, IBPS SO, RRB, Railways, Civil Services etc.
 Q1
Q1
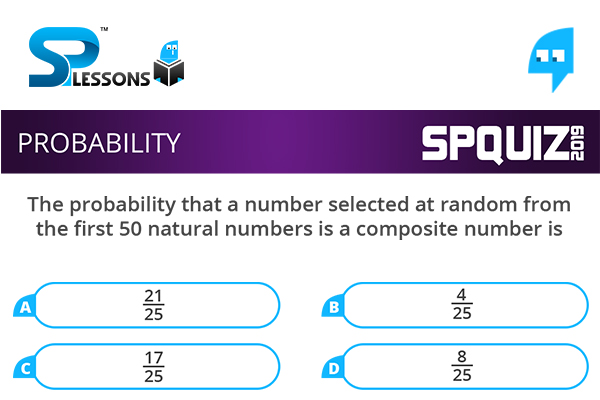
The probability that a number selected at random from the first 50 natural numbers is a composite number is
- A. [latex]\frac {21}{25}[/latex]
B. [latex]\frac {4}{25}[/latex]
C. [latex]\frac {17}{25}[/latex]
D. [latex]\frac {8}{25}[/latex]
The number of exhaustive events = [latex]^{50}{C}_{1}[/latex] = 50.
We have 15 primes from 1 to 50.
Number of favorable cases are 34.
Required probability = [latex]\frac {34}{50}[/latex] = [latex]\frac {17}{25}[/latex].
 Q2
Q2
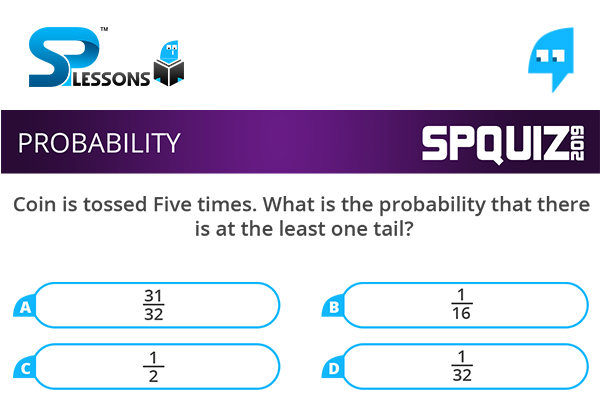
Coin is tossed Five times. What is the probability that there is at the least one tail?
- A. [latex]\frac {31}{32}[/latex]
B. [latex]\frac {1}{16}[/latex]
C. [latex]\frac {1}{2}[/latex]
D. [latex]\frac {1}{32}[/latex]
Let P(T) be the probability of getting least one tail when the coin is tossed five times.
[latex]P \bar{(T)}[/latex] = There is not even a single tail.
i.e. all the outcomes are heads.
[latex]P \bar{(T)}[/latex] = [latex]\frac {1}{32}[/latex] ; P(T) = 1 - [latex]\frac {1}{32}[/latex] = [latex]\frac {31}{32}[/latex]
 Q3
Q3
If a number is chosen at random from the set {1, 2, 3, ...., 100}, then the probability that the chosen number is a perfect cube is -
- A. [latex]\frac {1}{25}[/latex]
B. [latex]\frac {1}{2}[/latex]
C. [latex]\frac {4}{13}[/latex]
D. [latex]\frac {1}{10}[/latex]
We have 1, 8, 27 and 64 as perfect cubes from 1 to 100.
Thus, the probability of picking a perfect cube is
[latex]\frac {4}{100}[/latex] = [latex]\frac {1}{25}[/latex].
 Q4
Q4
Out of first 20 natural numbers, one number is selected at random. The probability that it is either an even number or a prime number is
- A. [latex]\frac {1}{2}[/latex]
B. [latex]\frac {16}{19}[/latex]
C. [latex]\frac {4}{5}[/latex]
D. [latex]\frac {17}{20}[/latex]
n(S) = 20
n(Even no) = 10 = n(E)
n(Prime no) = 8 = n(P)
P(EᴜP) = [latex]\frac {10}{20}[/latex] + [latex]\frac {8}{20}[/latex] - [latex]\frac {1}{20}[/latex] = [latex]\frac {17}{20}[/latex]
 Q5
Q5
If two dice are thrown together, the probability of getting an even number on one die and an odd number on the other is -
- A. [latex]\frac {1}{4}[/latex]
B. [latex]\frac {1}{2}[/latex]
C. [latex]\frac {3}{4}[/latex]
D. [latex]\frac {3}{5}[/latex]
The number of exhaustive outcomes is 36.
Let E be the event of getting an even number on one die and an odd number on the other. Let the event of getting either both even or both odd then = [latex]\frac {18}{36}[/latex] = [latex]\frac {1}{2}[/latex]
P(E) = 1 - [latex]\frac {1}{2}[/latex] = [latex]\frac {1}{2}[/latex].