SP Quiz - SPLessons
boy2

Probability – Quiz 6

Home > > Tutorial
SPLessons 5 Steps, 3 Clicks
5 Steps - 3 Clicks

Probability – Quiz 6

shape Introduction

Probability is one of important topic in Quantitative Aptitude Section. In Probability – Quiz 6 article candidates can find questions with answer. By solving this questions candidates can improve and maintain, speed, and accuracy in the exams. Probability - Quiz 6 questions are very useful for different exams such as IBPS PO, Clerk, SSC CGL, SBI PO, NIACL Assistant, NICL AO, IBPS SO, RRB, Railways, Civil Services etc.

shape Q1

A card is drawn from a pack of 52 cards. The probability of getting a queen of club or a king of heart is:
    A. [latex]\frac{1}{13}[/latex] B. [latex]\frac{2}{13}[/latex] C. [latex]\frac{1}{26}[/latex] D. [latex]\frac{1}{52}[/latex]

SPLessons

Here, n(S) = 52.
Let E = event of getting a queen of club or a king of heart.
Then, n(E) = 2.
i.e, P(E) = [latex]\frac {n(E)}{n(S)} = \frac {2}{52} = \frac {1}{26}[/latex]

shape Q2

If four coins are tossed, the probability of getting two heads and two tails is -
    A. [latex]\frac{3}{8}[/latex] B. [latex]\frac{6}{1}[/latex] C. [latex]\frac{1}{2}[/latex] D. [latex]\frac{1}{5}[/latex]

SPLessons

Since four coins are tossed, sample space = [latex]{2}^{4}[/latex]
Getting two heads and two tails can happen in six ways.
n(E) = six ways
p(E) = [latex]\frac{6}{{2}^{4}} = \frac {3}{8}[/latex]

shape Q3

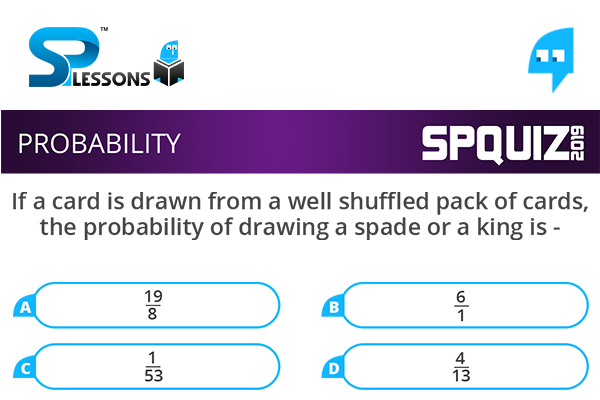
If a card is drawn from a well shuffled pack of cards, the probability of drawing a spade or a king is -
    A. [latex]\frac{19}{8}[/latex] B. [latex]\frac{6}{1}[/latex] C. [latex]\frac{1}{53}[/latex] D. [latex]\frac{4}{13}[/latex]

SPLessons

P(SᴜK) = P(S) + P(K) - P(S∩K), where S denotes spade and K denotes king.
P(SᴜK) = [latex]\frac{13}{52} + \frac{4}{52} - \frac{1}{52} = \frac{4}{13}[/latex]

shape Q4

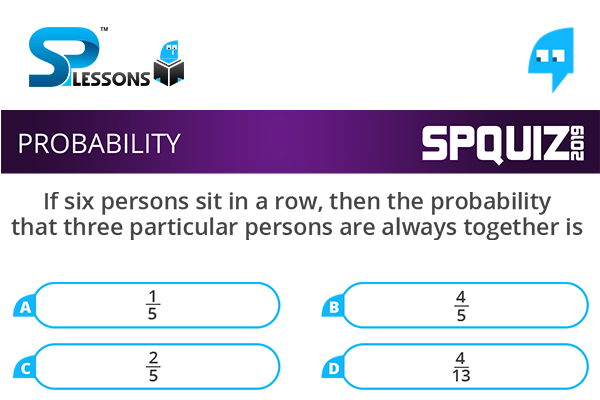
If six persons sit in a row, then the probability that three particular persons are always together is
    A. [latex]\frac{1}{5}[/latex] B. [latex]\frac{4}{5}[/latex] C. [latex]\frac{2}{5}[/latex] D. [latex]\frac{4}{13}[/latex]

SPLessons

Six persons can be arranged in a row in 6! ways. Treat the three persons to sit together as one unit then there four persons and they can be arranged in 4! ways. Again three persons can be arranged among them selves in 3! ways. Favourable outcomes = 3!4! Required probability = [latex]\frac{3!4!}{6!}[/latex] = [latex]\frac{1}{5}[/latex]

shape Q5

A basket has 5 apples and 4 oranges. Three fruits are picked at random. The probability that at least 2 apples are picked is -
    A. [latex]\frac{25}{42}[/latex] B. [latex]\frac{9}{20}[/latex] C. [latex]\frac{41}{45}[/latex] D. [latex]\frac{44}{13}[/latex]

SPLessons

Since there must be at least two apples,
[latex]\frac {^{5}{C}_{2} \times ^{4}{C}_{1}}{^{9}{C}_{3}} + \frac {^{5}{C}_{3}}{^{9}{C}_{3}} = \frac {25}{42}[/latex]
Hide Index Show Index