Introduction
Introduction
Ratios and Proportions is one of important topic in Quantitative Aptitude Section. In Ratios and Proportions Quiz 11 article candidates can find questions with an answer. By solving this questions candidates can improve and maintain, speed, and accuracy in the exams. Ratios and Proportions Quiz 11 questions are very useful for different exams such as IBPS PO, Clerk, SSC CGL, SBI PO, NIACL Assistant, NICL AO, IBPS SO, RRB, Railways, Civil Services etc.
 Q1
Q1
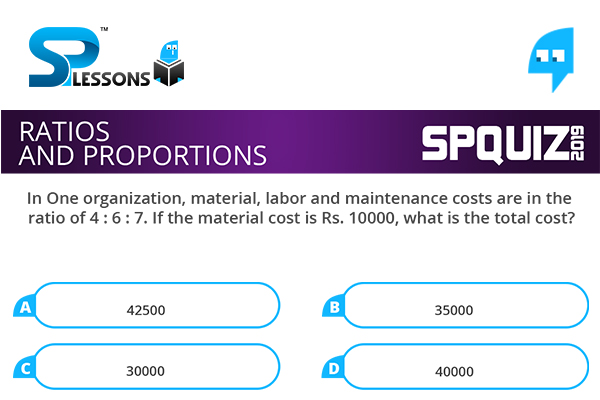
In One organization, material, labor and maintenance costs are in the ratio of 4 : 6 : 7. If the material cost is Rs. 10000, what is the total cost?
- A. 42500
B. 35000
C. 30000
D. 40000
Let us take the cost of material, labor and maintenance cost as 4m, 6m and 7m respectively.
Hence, we have total cost = 4m + 6m + 7m = 17m
Hence, we have 4m = 10000
[latex]\Rightarrow m = \frac {10000}{4} = 2500[/latex]
Then we have total cost = 2500 × 17 = 42500
 Q2
Q2
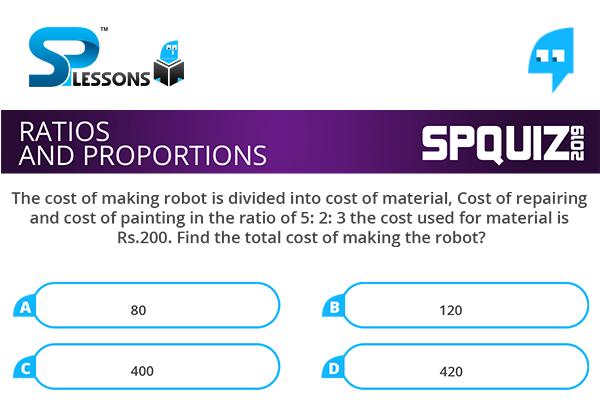
The cost of making robot is divided into cost of material, Cost of repairing and cost of painting in the ratio of 5: 2: 3 the cost used for material is Rs.200. Find the total cost of making the robot?
- A. 80
B. 120
C. 400
D. 420
From the given problem
Robot making cost = cost of material + cost of repairing + cost of painting
These three costs are in the ratio of 5: 2: 3
So assume cost of material is 5x, cost of repairing is 2x and cost of painting = 3x
Total cost for making the robot = 5X + 2X + 3X = 10X
According to the question,
Cost used for material = 200
[latex]\Rightarrow[/latex] 5x = 200
[latex]\Rightarrow[/latex] X = 40
Total cost for making robot = 10X
[latex]\Rightarrow[/latex] 10 × 40 = 400
∴ Total cost for making robot = Rs. 400
 Q3
Q3
The ratio between two numbers is 3 : 4 and their sum is 420. What is the greater of the two numbers?
- A. 175
B. 315
C. 200
D. 240
Since the 2 numbers are in the ratio 3 : 4,
Hence, let these two numbers be 3m and 4m.
We are given that 3m + 4m = 420
[latex]\Rightarrow[/latex] 7m = 420
[latex]\Rightarrow[/latex] m = [latex] \frac {420}{7}[/latex]
[latex]\Rightarrow[/latex] m = 60
Now, larger number = 4m = 4 × 60
= 240
 Q4
Q4
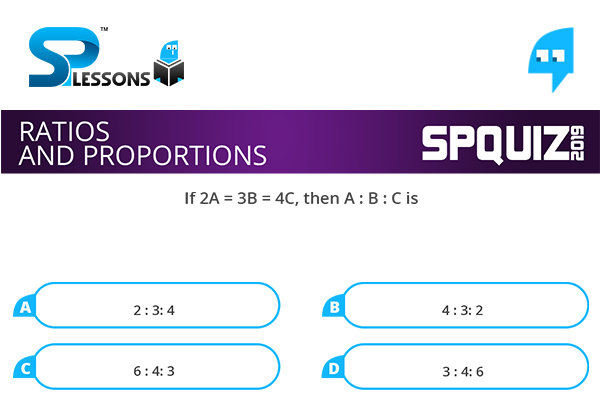
If 2A = 3B = 4C, then A : B : C is
- A. 2 : 3: 4
B. 4 : 3: 2
C. 6 : 4: 3
D. 3 : 4: 6
Given [latex]\Rightarrow[/latex] 2A = 3B = 4C
[latex]\Rightarrow[/latex] 2A = 3B ,
[latex]\Rightarrow \frac {A}{B} = (\frac {3}{2}) = (\frac {6}{4})[/latex]
[latex]\Rightarrow[/latex] A : B = 6 : 4 ....... (i)
&
[latex]\Rightarrow[/latex] 3B = 4C,
[latex]\Rightarrow \frac {B}{C} = (\frac {4}{3}) [/latex]
[latex]\Rightarrow[/latex] B : C = 4 : 3 ....... (ii)
From Equations (i) & (ii)
[latex]\Rightarrow[/latex] A : B : C = 6 : 4 : 3
 Q5
Q5
Capacity of a cylindrical vessel is 25.872 litres. If the height of the cylinder is 200% more than the radius of its base, what is the area of the base in square cms?
- A. 335.0
B. 1232.0
C. 616.0
D. None of these
∵ 1 Litre = 1000 Cubic Cms
[latex]\Rightarrow[/latex] 25.872 litres = 25872 Cubic Cms
The Volume of a Cylinder = [latex] π × {(Radius of Base)}^{2} [/latex]× Height of the Cylinder
Let the Radius of the Base = r
∵ The Height of the Cylinder = 200% more than r
∴ Height = r + 2r = 3r
[latex]\Rightarrow[/latex] Volume = [latex](\frac {22}{7}) × 3 × {r}^{3} = 25872[/latex]
[latex]\Rightarrow[/latex] r = 14 cms
[latex]\Rightarrow[/latex] Area of the Base = [latex]π × {(Radius of Base)}^{2} = (\frac {22}{7}) × 14 × 14 = 616 [/latex] Sq. cms