Introduction
Introduction
Partnership Quiz 3 chapter deals with profit and loss related problems. Profit and/or loss is shared among the partners based on the sum of money invested by individual partners and the time period of the investment.
For example: A partner who has invested the highest amount of money/resources will receive the highest share of the profit at the end of the year provided all the partners have invested for the same time period.
Ratio of Division of Gains:
1. Suppose A and B invest Rs. [latex]x[/latex] and Rs. [latex]y[/latex] respectively for a year in a business, then at the end of the year:
(A's share of profit) : (B's share of profit) = [latex]x[/latex] : [latex]y[/latex]
Here investment of all partners are for same time, and the gain or loss is distributed among them in the ratios of their investments.
2. Suppose A invests Rs. [latex]x[/latex] for 'p' months and B invests Rs. [latex]y[/latex] for 'q' months, then
(A's share of profit) : (B's share of profit) = [latex]x[/latex]p : [latex]x[/latex]q
Here investments are for different time periods, equivalent capitals are calculated for a unit of time by taking,
(capital x number of units of time).
Profit or loss is divided in the ratio of these capitals.
Working partner: The partner one who works for the business is called a working partner.
Sleeping partner: The partner who simply invests the money for the business and doesn't work is called a sleeping partner.
Concept 1: If a group of n persons invested different amount for different period then their profit is the ratio is [latex]At_{1}[/latex] : [latex]Bt_{2} [/latex] : [latex]Ct_{3} [/latex] : [latex]Ct_{3} [/latex] : [latex]Dt_{4} [/latex] : …… : [latex]Xt_{n} [/latex]
Here first person invested amount A for [latex]t_{1} [/latex] period, second persons invested amount B for [latex]t_{2} [/latex] period and so on.  Q1
Q1
A, B and C invested Rs 1000 for 8 months, Rs 1200 for 6 months and Rs 1500 for some months. Out of a total profit of Rs. 5,675 as profit, A received Rs 2000. For how much months did C invested?
- A. 7
B. 4
C. 5
D. 6
[latex]1000 \times : 1200 \times 6 : 1500 \times x[/latex]
80 : 72 : 15x
So [latex]\frac {80}{(80 + 72 + 15x} \times 5675 = 2000[/latex]
Solve, x = 5
 Q2
Q2
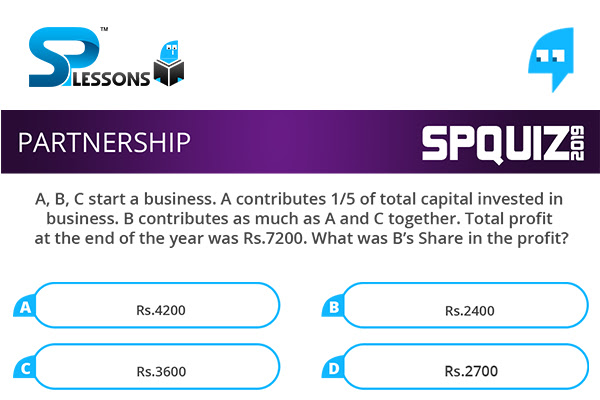
A, B, C start a business. A contributes 1/5 of total capital invested in business. B contributes as much as A and C together. Total profit at the end of the year was Rs.7200. What was B’s Share in the profit?
- A. Rs.4200
B. Rs.2400
C. Rs.3600
D. Rs.2700
A = [latex]\frac {x}{5} [/latex]
Remaining = [latex]\frac {4X}{5} = B + C[/latex]
B = [latex]\frac {X}{2} [/latex], C = [latex]\frac {4X}{5} - \frac {x}{2} = \frac {3x}{10} [/latex]
[latex]\frac {x}{5} : \frac {x}{2} : \frac {3x}{10} = 2 : 5 : 3[/latex]
[latex]\frac {7200 \times 5}{10} = 3600[/latex]
 Q3
Q3
Prabu, Hari and Riya started a business in partnership by investing Rs.38500, Rs.49500 and X respectively. At the end of the year they earned a total profit of Rs.101500 and Riya’s share in the profit is 45500 find X?
- A. Rs.71500
B. Rs.50200
C. Rs.40000
D. Rs.75000
X = 71500
[latex]38500 \times 12 : 49500 \times 12 : x \times 12 = 7 : 9 : 12x = 7 : 9 : 13[/latex]
Profit = [latex] \frac {101500 \times 13}{29} = 45500[/latex]
 Q4
Q4
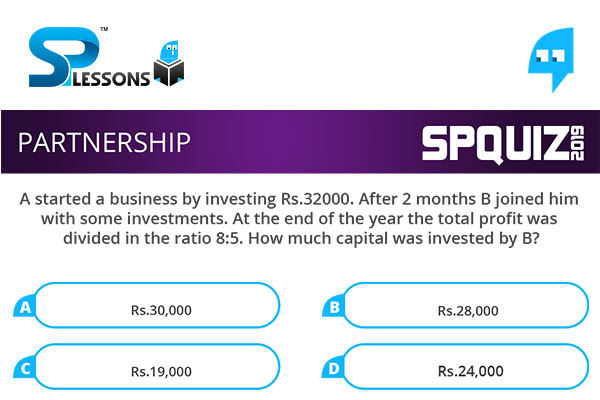
A started a business by investing Rs. 32000. After 2 months B joined him with some investments. At the end of the year the total profit was divided in the ratio 8:5. How much capital was invested by B?
- A. Rs.30,000
B. Rs.28,000
C. Rs.19,000
D. Rs.24,000
[latex]\frac {32000 \times 12}{x \times 10} = \frac {8}{5}[/latex]
19,20,000 = 80x
x = [latex]\frac {1920000}{80} = 24,000[/latex]
 Q5
Q5
A Company makes a profit of Rs.7,60,000, 20% of which is paid as taxes. If the rest is divided among the partners X, Y and Z in the ratio 5:3:4 then the share of X is
- A. Rs.1,40,000
B. Rs.1,52,000
C. Rs.1,20,000
D. Rs.2,00,000
20% = [latex] \frac {760000 \times 20}{100} = 152000 [/latex]
Remaining = Rs.6,08,000
x = [latex]\frac {608000 \times 3}{12} = 1,52000[/latex]