Introduction
Mensuration is one of important topic in Quantitative Aptitude Section. In Mensuration – Quiz 5 article candidates can find questions with an answer. By solving this questions candidates can improve and maintain, speed, and accuracy in the exams. Mensuration – Quiz 5 questions are very useful for different exams such as IBPS PO, Clerk, SSC CGL, SBI PO, NIACL Assistant, NICL AO, IBPS SO, RRB, Railways, Civil Services etc.
Q1
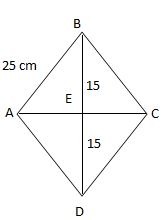
Find the area of a rhombus whose side is 25 cm and one of the diagonals is 30 cm?
Consider the rhombus ABCD. Let the diagonals intersect at E. Since
diagonals bisect at right angles in a rhombus.
[latex]{(BE)}^{2}[/latex] + [latex]{(AE)}^{2}[/latex] = [latex]{(AB)}^{2}[/latex]
[latex]{(25)}^{2}[/latex] = [latex]{(15)}^{2}[/latex] + [latex]{(AE)}^{2}[/latex] AE = [latex]\sqrt {(625 - 225)}[/latex] = [latex]\sqrt {400}[/latex] = 20
AC = 20 + 20 = 40 cm.
Area of a rhombus = [latex]\frac {1}{2} \times {d}_{1}{d}_{2}[/latex]
= [latex]\frac {1}{2} \times 40 \times 30[/latex] = 600 sq.cm.
- A. 225 sq.m
B. 360 sq.m
C. 720 sq.m
D. 600 sq.m
Q2
The percentage increase in the area of a rectangle, if each of its sides is increased by 20% is:
- A. 40%
B. 42%
C. 44%
D. 46%
Q3
The sector of a circle has radius of 21 cm and central angle 1350. Find its perimeter?
- A. 91.5 cm
B. 93.5 cm
C. 94.5 cm
D. 92.5 cm
Perimeter of the sector = length of the arc + 2(radius)
= [latex](\frac {135}{360} \times 2 \times \frac {22}{7} \times 21)[/latex] + 2(21)
= 49.5 + 42 = 91.5 cm
Q4
A chord AB of a circle of radius 5.25 cm makes an angle of 60∘ at the centre of the circle. Find the area of the major segment.
- A. 168 [latex]{cm}^{2}[/latex]
B. 100 [latex]{cm}^{2}[/latex]
C. 84 [latex]{cm}^{2}[/latex]
D. 70 [latex]{cm}^{2}[/latex]
The given circle is an equivlateral triangle
Area of the minor sector
= [latex]\frac {60}{360} \times \pi \times {(5.25)}^{2}[/latex]
= 14.4375 [latex]{cm}^{2}[/latex]
Area of the triangle
= [latex]\frac {\sqrt {3}}{4} \times {(5.25)}^{2}[/latex]
= 11.93 [latex]{cm}^{2}[/latex]
Area of the minor segment = Area of the minor sector - Area of the triangle
= 2.5 [latex]{cm}^{2}[/latex]
Area of the major segment = Area of the circle - Area of the minor segment
= 86.54 [latex]{cm}^{2}[/latex] − 2.5 [latex]{cm}^{2}[/latex]
= 84 [latex]{cm}^{2}[/latex]
Q5
A cone and a hemisphere have equal bases and equal volumes. Find the ratio of their heights
- A. 1 : 2
B. 2 : 1
C. 3 : 1
D. 3 : 4
Volume of the cone
= [latex]\frac {\pi {r}^{2} h}{3}[/latex]
= Volume of a hemisphere
= [latex]\frac {2 \pi {r}^{3}}{3}[/latex]
Height of a hemisphere = Radius of its base
By the above formula, we can see that h : r = 2 : 1