Introduction
Introduction
Permutation and Combination is one of important topic in Quantitative Aptitude Section. In Permutation and Combination Quiz 15 article candidates can find questions with answer. By solving this questions candidates can improve and maintain, speed, and accuracy in the exams. Permutation and Combination Quiz 15 questions are very useful for different exams such as IBPS PO, Clerk, SSC CGL, SBI PO, NIACL Assistant, NICL AO, IBPS SO, RRB, Railways, Civil Services etc.
 Q1
Q1
In how many different ways can any 4 letters of the word 'WORKING' be arranged?
- A. 5040
B. 840
C. 24
D. 120
There are 7 different letters in the word 'WORKING'.
Therefore, the number of arrangements of any 4 out of seven letters of the word = Number of all permutations of 7 letters, taken 4 at a time
[latex]^{n}{P}_{r}[/latex] = n(n - 1)(n - 2) ... (n - r + 1)
Here, n = 7 and r = 4, then we have
[latex]^{7}{P}_{4}[/latex] = 7 x 6 x 5 x 4 = 840.
Hence, the required number of ways is 840.
 Q2
Q2
In how many different ways can the letters of the word 'ARRANGEMENT' be arranged?
- A. 2494800
B. 4989600
C. 831600
D. none of these.
There are 11 different letters in the word 'ARRANGEMENT', in which A occurs 2 times, R occurs 2 times, n occurs 2 times and E occurs 2 times.
Therefore, the number of different arrangements of 11 letters of the word = [latex]\frac {n!}{(p1!)(p2!).....(pr!)}[/latex]
Here, n = 11, p1 = 2, p2 = 2, p3 = 2 and p4 = 2.
Then, [latex]\frac {11!}{2! 2! 2! 2!} = \frac {11!}{16} [/latex]= 2494800.
Hence, the required number of ways is 2494800.
 Q3
Q3
In how many different ways can the letters of the word 'DIGEST' be arranged such that the vowels may appear in the even places?
- A. 30
B. 720
C. 144
D. 24
There are 4 consonants and 2 vowels in the word DIGEST.
Out of 6 places, 3 places odd and 3 places are even.
2 vowels can arranged in 3 even places in [latex]^{3}{p}_{2}[/latex] ways = 3 x 2 = 6 ways.
And then 4 consonants can be arranged in the remaining 4 places in [latex]^{4}{p}_{4}[/latex] ways = 4! = 24 ways.
Hence, the required number of ways = 6 x 24 = 144.
 Q4
Q4
In how many different ways can the letters of the word "CHARGES" be arranged in such a way that the vowels always come together?
- A. 1440
B. 720
C. 360
D. 240
The arrangement is made in such a way that the vowels always come together.
i.e., "CHRGS(AE)".
Considering vowels as one letter, 6 different letters can be arranged in 6! ways; i.e., 6! = 720 ways.
The vowels "AE" can be arranged themselves in 2! ways; i.e.,2! = 2 ways
Therefore, required number of ways = 720 x 2 = 1440 ways.
 Q5
Q5
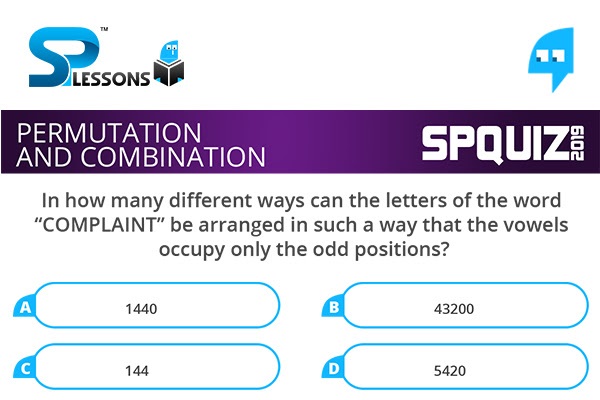
In how many different ways can the letters of the word "COMPLAINT" be arranged in such a way that the vowels occupy only the odd positions?
- A. 1440
B. 43200
C. 144
D. 5420
There are 9 different letters in the given word "COMPLAINT", out of which there are 3 vowels and 6 consonants.
Let us mark these positions as under:
[1] [2] [3] [4] [5] [6] [7] [8] [9]
Now, 3 vowels can be placed at any of the three places out of 5 marked 1, 3, 5, 7 and 9.
Number of ways of arranging the vowels = [latex]^{5}{P}_{3}[/latex] = 5 x 4 x 3 = 60 ways.
Also, the 6 consonants at the remaining positions may be arranged in [latex]^{6}{P}_{6}[/latex] ways = 6! ways = 720 ways.
Therefore, required number of ways = 60 x 720 = 43200 ways.