Introduction
Introduction
Mensuration is one of important topic in Quantitative Aptitude Section. In Mensuration Quiz 14 article candidates can find a question with an answer. By solving this question candidates can improve and maintain, speed, and accuracy in the exams. Mensuration Quiz 14 questions a very useful for different exams such as IBPS PO, Clerk, SSC CGL, SBI PO, NIACL Assistant, NICL AO, IBPS SO, RRB, Railways, Civil Services etc.
 Q1
Q1
The total cost of flooring a room at Rs 12.50 per sq m is 450. If the length of the room is 6 m, its breadth is
- A. 5 m
B. 9 m
C. 8 m
D. 6 m
∵The flooring area of the room = [latex]\frac {Total cost of flooring room}{Rate per sq m}[/latex]
= [latex]\frac {450}{12.50} {m}^{2} = 36 {m}^{2}[/latex]
∵The length of the room = 6 m
∴The breadth of the room = [latex]\frac {Area}{Length} \frac{36}{6} = 6 m[/latex]
Hence, breadth of the room = 6 m
 Q2
Q2
Find the volume of a cuboid of dimensions 16 cm x 10 cm x 6 cm.
- A. 96
B. 960
C. 9600
D. 4800
Volume of cuboid = l x b x h = 16 x 10 x 6 = 960 [latex]{cm}^{3}[/latex]
 Q3
Q3
The radius of two circles is 13cm and 6cm respectively. What is the radius of the circle which has circumference equal to the sum of the circumference of two circles?
- A. 21 cm
B. 19 cm
C. 17 cm
D. 42 cm
Circumference of a circle with radius r = 2rπ
Now sum of the circumference of two circle with radius 13cm and 8cm respectively
= 2π (13+6) = [latex] \frac {2 \times 22 \times 19}{7} [/latex] = 38π
Now the another circle whose circumference is 152 cm has radius = R
Hence 2πR = 38π
R = [latex]\frac {38π}{2π}[/latex] = 19 cm
 Q4
Q4
How many days will a cow take to graze the grass of a square field of side 30 m, if it grazes 25 m^2 are everyday?
- A. 33
B. 34
C. 35
D. 36
Area of square field = [latex]{(side)}^{2}[/latex]
= [latex]{(30)}^{2}[/latex]= 900 sq m
Required number of days = [latex]\frac {Area of square field}{area grazed in one day} = \frac {900}{25} = 36[/latex]
 Q5
Q5
The area of a rhombus is 96 cm and the length of its one diagonal is 12 cm. The perimeter (in cm) of the rhombus is
- A. 40
B. 60
C. 192
D. 100
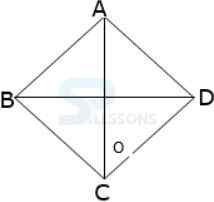
Let ABCD be a rhombus, all sides of rhombus equal and its diagonal cuts each other at right angle.
Let AC = 12cm
Area of rhombus = [latex]\frac {1}{2}[/latex] (product of diagonals) = [latex]\frac {1}{2}[/latex] (AC × BD)
96 = [latex]\frac {1}{2}[/latex] (12 × BD) Ã 12 × BD = 192 Ã BD = 16 cm
Now in right angled triangle AOB
[latex]{AB}^{2} = {AO}^{2} + {BO}^{2}; AO = \frac {1}{2}[/latex](AC) = 6 cm; BO [latex]\frac {1}{2}[/latex] (BD) = 8cm
[latex]{AB}^{2} = {6}^{2} + {8}^{2}[/latex] = 36 + 64 = 100 Ã AB = 10cm
Hence perimeter of rhombus = 4 × side = 4 × 10 = 40cm