Introduction
Introduction
What is data interpretation?
Data Interpretation or DI refers to the implementation of procedures through which data is reviewed for the purpose of arriving at an inference. Data can be obtained from multiple sources.
Example: data from running of industries, census population data etc.
Data Interpretation is one of important topic in Quantitative Aptitude Section. In Data Interpretation Quiz 9 article candidates can find questions with answer. By solving this questions candidates can improve and maintain, speed, and accuracy in the exams. Data Interpretation Quiz 9 questions are very useful for different exams such as IBPS PO, Clerk, SSC CGL, SBI PO, NIACL Assistant, NICL AO, IBPS SO, RRB, Railways, Civil Services etc.
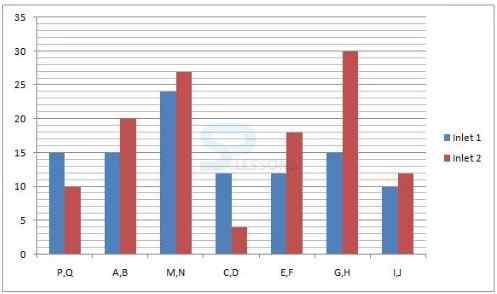
Direction(1-5): Study the following graph carefully and answer the following questions given below.
Time taken by the pipes to fill a tank/cistern (hours/minutes)
 Q1
Q1
A large cistern can be filled by two pipes P and Q. How many minutes will it take to fill the Cistern from an empty state if Q is used for half the time and P and Q fill it together for the other half?
- A. 6.5 minutes
B. 7.5 minutes
C. 8.5 minutes
D. 9.5 minutes
Part filled by P and Q = [latex]\frac {1}{15} + \frac {1}{10} = \frac {1}{6}[/latex]
Part filled by Q = [latex]\frac {1}{10}[/latex]
[latex]\frac {x}{2}(\frac {1}{6} + \frac {1}{10}) = \frac {2}{15} = \frac {15}{2} = [/latex] 7.5 minutes
 Q2
Q2
Two pipes M and N can fill a tank. If both the pipes are opened simultaneously, after how much time should N be closed so that the tank is full in 8 minutes?
- A. 14 minutes
B. 12 minutes
C. 15 minutes
D. 18 minutes
Required time [latex]= y (1 - (\frac {t}{x}) = 27 (1- (\frac {8}{24})) [/latex] = 18 minutes
 Q3
Q3
Two pipes C and D can fill a cistern. If they are opened on alternate minutes and if pipe C is opened first, in how many minutes will the tank be full?
- A. 4 minutes
B. 5 minutes
C. 2 minutes
D. 6 minutes
Pipe P can fill = [latex]\frac {1}{12}[/latex]
Pipe Q can fill = [latex]\frac {1}{4}[/latex]
For every two minutes, [latex]\frac {1}{12} + \frac {1}{4} = \frac {1}{3}[/latex] Part filled
Total = 6 minutes
 Q4
Q4
A waste pipe, W can carry off 12 litre of water per minute. If all the pipes I, J and W are opened when the tank is full and it takes one hour to empty the tank. Find the capacity of the tank.
- A. 30
B. 45
C. 60
D. 75
Let the waste pipe take ‘T’ time to empty the tank.
[latex] (\frac {1}{10} + \frac {1}{12} - \frac {1}{t}) \times 60[/latex] = -1
We will get T = 5 min
So capacity = 5 [latex]\times[/latex] 12 = 60 ltr
 Q5
Q5
Three pipes C, A and B can fill a tank. If pipe C is opened all the time and pipe A and B are opened for one hour alternatively. The tank will be full in
- A. 5 hr
B. 6 hr
C. 7 hr
D. 8 hr
[latex](\frac {1}{12} + \frac {1}{15}) + (\frac {1}{12} + \frac {1}{20}) = \frac {17}{60}[/latex] (in 2 hrs this much tank is filled)
So in 6 hrs [latex] \frac {51}{60}[/latex] is filled. Remaining, [latex] \frac {9}{60} = (\frac {1}{12} + \frac {1}{15}) \times t[/latex], so T = 1hr
So total = 6 + 1 = 7 hr