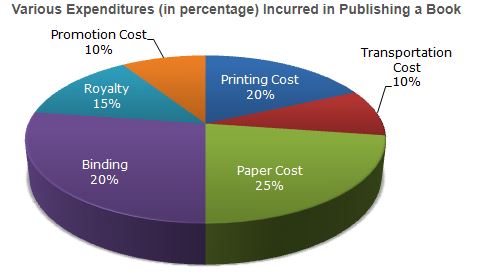
Directions (1 - 2):The following pie-chart shows the percentage distribution of the expenditure incurred in publishing a book. Study the pie-chart and the answer the questions based on it.

1. If for a certain quantity of books, the publisher has to pay Rs. 30,600 as printing cost, then what will be amount of royalty to be paid for these books

A. Rs. 19,450 B. Rs. 21,200 C. Rs. 22,950 D. Rs. 26,150

Answer: (C)
Solution: Let the amount of Royalty to be paid for these books be Rs. r. Then, 20 : 15 = 30600 : r => r = Rs [latex]\frac{30600 × 15}{20}[/latex] = Rs. 22,950.
2. The price of the book is marked 20% above the C.P. If the marked price of the book is Rs. 180, then what is the cost of the paper used in a single copy of the book?

A. Rs. 36 B. Rs. 37.50 C. Rs. 42 D. Rs. 44.25

Answer: (B)
Solution: Clearly, marked price of the book = 120% of C.P. Also, the cost of paper = 25% of C.P Let the cost of paper for a single book be Rs. n. Then, 120 : 25 = 180 : n => n = Rs. [latex]\frac{25 × 180}{120}[/latex] = Rs. 37.50 .

1. The sum and the product of the roots of the quadratic equation [latex]{x}^{2}[/latex] + 20x + 3 = 0 are?

A. 10, 3 B. -10, 3 C. 20, -3 D. -10, -3

Answer: E
Solution: Sum of the roots and the product of the roots are -20 and 3 respectively.
2. If the roots of the equation 2[latex]{x}^{2}[/latex] - 5x + b = 0 are in the ratio of 2:3, then find the value of b?

A. 3 B. 4 C. 5 D. 6

Answer: A
Solution: Let the roots of the equation 2a and 3a respectively. 2a + 3a = 5a = -(- [latex]\frac{5}{2}[/latex]) = [latex]\frac{5}{2}[/latex] => a = [latex]\frac{1}{2}[/latex] Product of the roots: 6[latex]{a}^{2}[/latex] = [latex]\frac{b}{2}[/latex] => b = 12[latex]{a}^{2}[/latex] a = [latex]\frac{1}{2}[/latex], b = 3.

1. Look at this series: 7, 10, 8, 11, 9, 12, ... What number should come next?

A. 7 B. 10 C. 12 D. 13 E. Both I and II are sufficient

Answer: B
Solution: This is a simple alternating addition and subtraction series. In the first pattern, 3 is added; in the second, 2 is subtracted.
2. Look at this series: 36, 34, 30, 28, 24, ... What number should come next?

A. 20 B. 22 C. 23 D. 26 E. Both I and II are sufficient

Answer: B
Solution: This is an alternating number subtraction series. First, 2 is subtracted, then 4, then 2, and so on.

Q1. A grocer has a sale of Rs. 6435, Rs. 6927, Rs. 6855, Rs. 7230 and Rs. 6562 for 5 consecutive months. How much sale must he have in the sixth month so that he gets an average sale of Rs. 6500?

A. Rs. 4991 B. Rs. 5991 C. Rs. 6001 D. Rs. 6991

Answer: A
Solution: Total sale for 5 months = Rs. (6435 + 6927 + 6855 + 7230 + 6562) = Rs. 34009. Required sale = Rs. [ (6500 x 6) - 34009 ] = Rs. (39000 - 34009) = Rs. 4991.
Q2. The average of 20 numbers is zero. Of them, at the most, how many may be greater than zero?

A. 0 B. 1 C. 10 D. 19

Answer: D Solution: Average of 20 numbers = 0. Sum of 20 numbers (0 x 20) = 0. It is quite possible that 19 of these numbers may be positive and if their sum is a then 20th number is (-a).

Q1. The length of a rectangle is two - fifths of the radius of a circle. The radius of the circle is equal to the side of the square, whose area is 1225 sq.units. What is the area (in sq.units) of the rectangle if the rectangle if the breadth is 10 units?

A. 140 B. 156 C. 175 D. 214

Answer: A
Solution: Explanation: Given that the area of the square = 1225 sq.units => Side of square = √1225 = 35 units The radius of the circle = side of the square = 35 units Length of the rectangle = [latex]\frac{2}{5}[/latex] * 35 = 14 units Given that breadth = 10 units Area of the rectangle = lb = 14 * 10 = 140 sq.units
Q2. The sector of a circle has radius of 21 cm and central angle 135o. Find its perimeter?

A. 91.5 cm B. 93.5 cm C. 94.5 cm D. 92.5 cm

Answer: A
Solution: Perimeter of the sector = length of the arc + 2(radius) = ([latex]\frac{135}{360}[/latex] * 2 * [latex]\frac{22}{7}[/latex] * 21) + 2(21) = 49.5 + 42 = 91.5 cm

Q1. Two students appeared at an examination. One of them secured 9 marks more than the other and his marks was 56% of the sum of their marks. The marks obtained by them are:

A. 39, 30 B. 41, 32 C. 42, 33 D. 43, 34

Answer: C
Solution: Let their marks be (x + 9) and x. Then, x + 9 = [latex]\frac{56}{100}[/latex] (x + 9 + x) 25(x + 9) = 14(2x + 9) 3x = 99 x = 33 So, their marks are 42 and 33.
Q2. The sector of a circle has radius of 21 cm and central angle 135o. Find its perimeter?

A. 91.5 cm B. 93.5 cm C. 94.5 cm D. 92.5 cm

Answer: A
Solution: Perimeter of the sector = length of the arc + 2(radius) = ([latex]\frac{135}{360}[/latex] * 2 * [latex]\frac{22}{7}[/latex] * 21) + 2(21) = 49.5 + 42 = 91.5 cm

Q1. If a person walks at 14 km/hr instead of 10 km/hr, he would have walked 20 km more. The actual distance travelled by him is:

A. 50 km B. 56 km C. 70 km D. 80 km

Answer: A
Solution: Let the actual distance travelled be x km. Then, [latex]\frac{x}{10}[/latex] = [latex]\frac{x + 20}{14}[/latex] 14x = 10x + 200 4x = 200 x = 50 km.
Q2. Excluding stoppages, the speed of a bus is 54 kmph and including stoppages, it is 45 kmph. For how many minutes does the bus stop per hour?

A. 9 B. 10 C. 12 D. 20

Answer: B
Solution: Due to stoppages, it covers 9 km less. Time taken to cover 9 km = [latex]\frac{9}{54}[/latex] X 60 min = 10 min