Introduction
Introduction
"Trigonometry (from Greek trigōnon, "triangle" and metron, "measure") is a branch of mathematics that studies relationships between side lengths and angles of triangles."Trigonometry has found its importance in multiple fields. It has found its applications in the fields ranging from Engineering to Architecture to Astronomy as well. Trigonometry can be used in these fields by to measure distances and angles by assuming lines that connect the points. As a result, Trigonometric Ratios and Height and Distance are interconnected.
The article Trigonometric Ratios and Height and Distance Practice Quiz lists different types of Trigonometric Ratios and Height and Distance questions with solutions useful for candidates preparing for different competitive examinations like RRB ALP/Technical Exams/Junior Engineer Recruitment Exams, SSC, CAT and etc. [What is a Triangle?]
 Quiz
Quiz
1. If sin θ + cosec θ = 2, then [latex]{sin}^{2}θ + {cosec}^{2}θ [/latex]is equal to:
- A. 1
B. 4
C. 2
D. None of these
- A. sin 2θ
B. cos 2θ
C. cosec 2θ
D. sec 2θ
- A. tan B
B. 2 tan B
C. cot B
D. 2 cot B
- A. [latex]\frac{1}{x} + y[/latex]
B. [latex]\frac{1}{xy}[/latex]
C. [latex]\frac{1}{x} - \frac{1}{y}[/latex]
D. [latex]\frac{1}{x} + \frac{1}{y}[/latex]
- A. [latex]\frac{1}{\sqrt{5}}[/latex]
B. [latex] - \frac{1}{\sqrt{5}}[/latex]
C. [latex]\sqrt{\frac{2}{5}}[/latex]
D. -[latex]\sqrt{\frac{2}{5}}[/latex]
- A. 0
B. -1
C. 0
D. None of these
- A. [latex]\frac{1}{16}[/latex]
B. [latex]\frac{1}{32}[/latex]
C. [latex]\frac{1}{8}[/latex]
D. [latex]\frac{1}{4}[/latex]
- A. [latex]16{cos}^{3}x {sin}^{2}x[/latex]
B. [latex]16{sin}^{3}x {cos}^{2}x[/latex]
C. [latex]4{cos}^{3}x {sin}^{2}x[/latex]
D. [latex]4{sin}^{3}x {cos}^{2}x[/latex]
- A. sin 2θ
B. cos 2θ
C. tan 2θ
D. sec 2θ
- A. 30º
B. 45º
C. 60º
D. 90º
- A. 2a = b
B. a = b
C. a = 2b
D. None of these
- A. 0
B. 1
C. sin y
D. cos y
- A. [latex]\frac{\pi}{4}rad[/latex]
B. [latex]\frac{\pi}{3}rad[/latex]
C. [latex]\frac{\pi}{5}rad[/latex]
D. [latex]\frac{\pi}{10}rad[/latex]
- A. 1, -1
B. [latex]\frac{1}{2}[/latex], - [latex]\frac{1}{2}[/latex]
C. [latex]\frac{1}{4}[/latex], - [latex]\frac{1}{4}[/latex]
D. 2, -2
- A. 1 ≤ A ≤ 2
B. [latex]\frac{3}{4}[/latex] ≤ A ≤ 1
C. [latex]\frac{13}{16}[/latex] ≤ A ≤ 1
D. [latex]\frac{3}{4}[/latex] ≤ A ≤ [latex]\frac{13}{16}[/latex]
1. The value of [latex] {sin}^{2} 30º + {sin}^{2} 60º[/latex] is
- A. 1
B. [latex]\frac{3}{2}[/latex]
C. 2
D. [latex]\frac{3}{4}[/latex]
- A. 0
B. +oo
C. 1
D. undefined
- A. 9.2 m
B. 2.3 m
C. 6.9 m
D. 7.8 m
- A. 50 [latex]\sqrt{2}[/latex] m
B. 50 [latex]\sqrt{3}[/latex] m
C. [latex]\frac{50}{\sqrt{2}}[/latex]
D. [latex]\frac{50}{\sqrt{3}}[/latex]
- A. 30 [latex]\sqrt{3}[/latex] m
B. 10 [latex]\sqrt{3}[/latex] m
C. 15m
D. 6m
- A. 4 ([latex]\sqrt{3} - 1[/latex]) m
B. 2 ([latex] 2\sqrt{3} - 1[/latex]) m
C. 4 ([latex]\sqrt{3} + 1[/latex]) m
D. 2 ([latex] 2\sqrt{3} + 1[/latex]) m
- A. 7.5 m
B. 5 [latex] \sqrt{3}[/latex]) m
C. 15 ([latex]\frac {\sqrt{3}}{2}[/latex]) m
D. 10 ([latex] \sqrt{3}[/latex]) m
- A. 2 ([latex] \sqrt{3} + 1[/latex]) m
B. 3 ([latex] \sqrt{3} + 1[/latex]) m
C. 4([latex] \sqrt{3} + 1[/latex]) m
D. 2 ([latex] 2\sqrt{3} + 1[/latex]) m
- A. 4 m
B. 16 m
C. 16 [latex]\frac{\sqrt{3}}{3} [/latex]
D. 16 [latex] \sqrt{3} [/latex]
- A. 2 ([latex] \sqrt{3} + 1[/latex]) m
B. 3 ([latex] \sqrt{3} + 1[/latex]) m
C. 3 - ([latex] \sqrt{3} [/latex]) m
D. 3 + ([latex] \sqrt{3} [/latex]) m
- A. 7.5 m
B. [latex]5 \sqrt{3}[/latex] m
C. [latex]10 \sqrt{3}[/latex]m
D. [latex]\frac{15 \sqrt{3}}{2}[/latex] m
- A. [latex] 4 \frac {3 + \sqrt{3}}{3}[/latex] m
B. [latex] 4 (3 + \sqrt{3})[/latex] m
C. [latex] 2 \frac{1 + \sqrt{3}}{3}[/latex] m
D. [latex] 2 (1 + 2 \sqrt{3})[/latex] m
- A. 15 m
B. 10 [latex]\sqrt{3}[/latex] m
C. 30 m
D. 30 [latex]\sqrt{3}[/latex] m
- A. 4 [latex]\sqrt{3}[/latex] m
B. 2 [latex](\sqrt{3} + 1)[/latex] m
C. 2 [latex](\sqrt{3} + 3)[/latex] m
D. 2 [latex]\sqrt{3} [/latex] m
- A. [latex]20 \frac{\sqrt{3}}{3}[/latex] m
B. [latex]40 \frac{\sqrt{3}}{3}[/latex] m
C. 20 m
D. 20[latex]\sqrt{3}[/latex] m
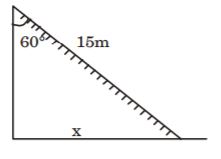
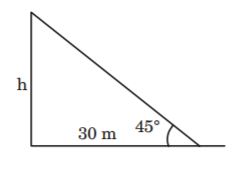
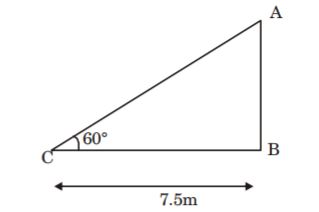
1. The angle of elevation of a ladder leaning against a wall is 60° and the foot of the ladder is 7.5 m away from the wall. The length of the ladder is
- A. 15 m
B. 14.86 m
C. 15. 64 m
D. 15.8 m
- A. 1
B. [latex]\frac{3}{4}[/latex]
C. [latex]\frac{3}{2}[/latex]
D. 3
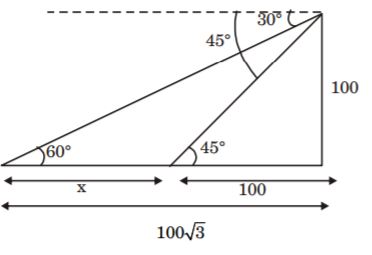
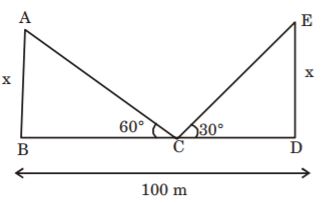
- A. 100([latex]\sqrt{3} + 1[/latex])
B. 100([latex]\sqrt{3} - 1[/latex])
C. ([latex]100 \sqrt{3} + 1[/latex])
D. ([latex]100 \sqrt{3} - 1[/latex])
- A. 2
B. [latex] \frac{\sqrt{15}}{4}[/latex]
C. [latex] \frac {4}{\sqrt{15}}[/latex]
D. 4
- A. 15 [latex]\sqrt{3}[/latex]
B. 30
C. 45
D. 20 [latex]\sqrt{3}[/latex]
- A. -5
B. -2
C. 1
D. 0
- A. 50 ([latex]\sqrt{3} - 1[/latex])
B. 50 ([latex]\sqrt{3} + 1[/latex])
C. 50([latex]3 - \sqrt{3} [/latex]) m
D. 50([latex]6 \sqrt{3} - 1[/latex]) m
- A. -2
B. -1
C. 1
D. 2
- A. 20 [latex]\sqrt{3}[/latex]
B. 20[latex]\sqrt{3}[/latex] + 1 m
C. 20[latex](\sqrt{3} - 1)[/latex] m
D. [latex]\frac{20 \sqrt{3} }{3} + 1[/latex] m
- A. 0
B. 1
C. -1
D. -2
- A. 25 [latex]\sqrt{3}[/latex]
B. 50 [latex]\sqrt {3}[/latex]
C. 25 [latex](\sqrt{3} - 1)[/latex]
D. 25 [latex](\sqrt{3} + 1)[/latex]
- A. 2, 3
B. 1, 3
C. 2, [latex]\frac{5}{2}[/latex]
D. 3, 4
- A. 40
B. 45 [latex]\sqrt{3}[/latex]
C. 60
D. 40 [latex]\sqrt{3}[/latex]
- A. [latex]\frac{1}{2}[/latex]
B. [latex]\frac{1}{4}[/latex]
C. [latex]\frac{2}{4}[/latex]
D. 1
- A. 70
B. 60 [latex]\sqrt{2}[/latex]
C. 50 [latex]\sqrt{2}[/latex]
D. 50