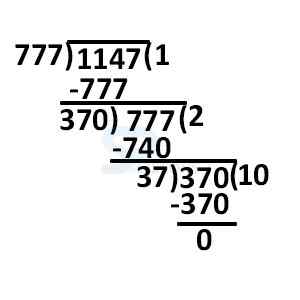L.C.M:
L.C.M stands for "Least Common Multiple". The least number which is exactly divisible by each one of the given numbers is referred as the L.C.M. of the numbers.
Factorization method: First list each one of the given numbers as the product of prime factors.Then multiply each factor the greatest number of times it occurs in either number. If the same factor occurs more than once in both numbers, you multiply the factor the greatest number of times it occurs.
Example 1: Find the least common multiple (L.C.M) of 9 and 15 by using prime factorization method.
Solution:

Step I:
Resolving each given number into its prime factors. 9 = 3 × 3 = [latex]3^{2}[/latex]. 15 = 3 × 5.

Step II:
The product of all the factors with highest powers. = [latex]3^{2}[/latex] × 5 = 3 × 3 × 5 = 45.

Step III:
The required least common multiple (L.C.M) of 9 and 15 = 45.

Example 2: What is the least common multiple (L.C.M) of 16 and 24 by using prime factorization method?
Solution:

Step I:
Resolving each given number into its prime factors. 16 = 2 x 2 x 2 x 2 = [latex]2^{4}[/latex] 24 = 2 x 2 x 2 x 3 = [latex]2^{3}[/latex] x 3

Step II:
The product of all the factors with highest powers. = [latex]2^{4}[/latex] × 3 = 2 × 2 x 2 × 2 × 3 = 48.

Step III:
The required least common multiple (L.C.M) of 16 and 24 = 48.

Division method: First arrange the given numbers in a horizontal row. Divide them by a suitable prime number, which exactly divides at-least two of the given numbers. Put the quotient directly down in the next row and if it is not divisible put the same number down. This is continued until the co-primes are left in the last row. In the end, we multiply all the prime numbers by which we have divided and the co-prime numbers left in the last row. The resultant product is the L.C.M.
Example 1: Find the L.C.M. of 12, 36 and 72.
Solution:

Keep dividing each row till there are no common factor except 1.



Multiply the dividers with the last row.
∴ L.C.M. (12, 36, 72) = 2 × 2 × 3 × 3 × 1 × 1 × 4 = 72.

Example 2: Find the L.C.M. of 16, 24, 26 and 54.
Solution:

∴ L.C.M. = 2 x 2 x 2 x 3 x 3 x 2 x 3 = 432.

H.C.F:
H.C.F stands for "Highest Common Factor". The greatest common factor of two or more whole numbers is referred as the H.C.F. of the numbers.
Factorization method: First list each one of the given numbers as the product of prime factors. Product of all common prime factors is the H.C.F.
Example: Find the H.C.F. of 12, 36 and 72
Solution:

• Factors of 12 = 2 × 2 × 3 = [latex]2^{2}[/latex] × 3


• Factors of 36 = 3 × 3 × 2 × 2 = [latex]2^{2}[/latex] × [latex]3^{2}[/latex]


• Factors of 72 = 2 × 2 × 3 × 3 × 2 = [latex]2^{3}[/latex] × [latex]3^{2}[/latex]

H.C.F. can be found by taking the product of least powers of all common factors that occur in these numbers.
∴ H.C.F. (12, 36, 72) = [latex]2^{2}[/latex] × 3 = 12.

Division method: Initially divide the larger number by the smaller number. Then the remainder is treated as the divisor and the divisor as dividend. Divide the first divisor by the first remainder and the second divisor by the second remainder. Process is continued until the remainder is zero.
Example: Find the H.C.F. of 12, 36 and 72.
Solution:

Keep dividing each row till one of the numbers becomes 1.



Multiply the dividers.
∴ H.C.F. (12, 36, 72) = 2 × 2 × 3 = 12.

Long Division Method:
Example: Find the H.C.F. of 777 and 1147.
Solution:

∴ H.C.F. (777, 1147) = 37.

Concept of Co-Primes: Two numbers are said to be Co-Primes, if they have no positive common factor, other than 1.
Example 1: Are 16 and 25 Co-primes
Solution:

Factors of 16: 1, 2, 4, 8, and 16
Factors of 25: 1, 5, and 25
Here, 16 and 25 have only one common factor that is 1. Hence, they are co-prime.

Example 2: Are 21 and 27 Co-primes
Solution:

Factors of 21: 1, 3, 7, and 21.
Factors of 27: 1, 2, 3, 9 and 27.
Here, 21 and 27 have only two common factors that is 1 and 3. Hence, they are NOT co-prime.

H.C.F. of Co-primes: Co-primes have H.C.F. as 1.
L.C.M. of Co-primes: L.C.M. of co-prime numbers = Product of co-prime numbers.

H.C.F. and L.C.M. for Decimals:
Example 1:
Find the H.C.F. of 1.20 and 22.5.
Solution:

Step 1: Convert each of the decimals to like decimals (decimals having same number of digits after the decimal point). We have, 1.20 and 22.5. Converting each of the following decimals into like decimals, we get 1.20 and 22.50.
Step 2: Remove the decimal point and find the H.C.F. as usual. So, after removing the decimals, we have 120 and 2250. ∴ H.C.F.(120, 2250) = 30.
Step 3: Put the decimal point exactly before as the number of decimal places obtained in the Step 1. ∴ H.C.F.(1.20, 22.5) = 0.30

Example 2:
Find the L.C.M. of 1.20 and 22.5.
Solution:

Step 1: Convert each of the decimals to like decimals (decimals having same number of digits after the decimal point). We have, 1.20 and 22.5. Converting each of the following decimals into like decimals, we get 1.20 and 22.50.
Step 2: Remove the decimal point and find the L.C.M. as usual. So, after removing the decimals, we have 120 and 2250. ∴ L.C.M.(120, 2250) = 9000.
Step 3: Put the decimal point exactly before as the number of decimal places obtained in the Step 1. ∴ L.C.M.(1.20, 22.5) = 90.00

Applications of H.C.F. and L.C.M:
There are various practical applications of H.C.F. and L.C.M. Let's take a look at a few examples to see them.
Example 1: Find the greatest number that will divide 400, 435 and 541 leaving 9, 10 and 14 as remainders, respectively.

Solution:

We can interpret “greatest number that will divide” as calculating G.C.D./H.C.F. of
numbers (400 - 9), (435 - 10), and (541 - 14) i.e. H.C.F.(391, 425, 527).

• Factors of 391: 1, 17, 23, 391


• Factors of 425: 1, 5, 17, 25, 425


• Factors of 527: 1, 17, 31, 527

Clearly, H.C.F.(391, 425, 527) = 17

Example 2: Mary, John and Curran start to jog around a circular stadium. They complete their rounds in 18 seconds, 24 seconds and 44 seconds, respectively. After how many seconds will they be together at the starting point?
Solution:

We can interpret “how many seconds will they be together at the starting point” as calculating L.C.M.(18, 24, 44).

• 18 = 2 × [latex]3^{2}[/latex]


• 24 = [latex]2^{3}[/latex] × 3


• 44 = [latex]2^{2}[/latex] × 11

Clearly, L.C.M.(18, 24, 44) = [latex]2^{3}[/latex] × [latex]3^{2}[/latex] × 11 = 792

Example 3: L.C.M. for comparing fractions Compare [latex]\frac{10}{9}[/latex], and [latex]\frac{7}{6}[/latex]
Solution:

Comparing these fractions is not a n easy task. Therefore, we use L.C.M. of the denominators to handle this.
Step - 1:Find the L.C.M. of the denominators of the given fractions. L.C.M. of denominators = L.C.M.(9, 6) = 18
Step - 2: Convert each of the fractions into an equivalent fraction with L.C.M. as the denominator. [latex]\frac{10}{9}[/latex] = [latex]\frac{10 \times 2}{9 \times 2}[/latex] = [latex]\frac{20}{18}[/latex] and [latex]\frac{7}{6}[/latex] = [latex]\frac{7 \times 3}{6 \times 3}[/latex] = [latex]\frac{21}{18}[/latex]
Step - 3:The resultant fraction with the greatest numerator is the greatest. ∴ as 20 < 21, [latex]\frac{10}{9}[/latex] < [latex]\frac{7}{6}[/latex].

The product of LCM and HCF of any two given natural numbers is equivalent to the product of the given numbers.
Suppose x and y are two numbers, then.
⇒ LCM (x & y) × HCF (x & y) = x × y
Example 1: Highest common factor and lowest common multiple of two numbers are 18 and 1782 respectively. One number is 162, find the other.
Solution:

We know, LCM × HCF = Product of the Numbers (First number × Second number) then we get,
18 × 1782 = 162 × Second number
18 × 1782/162 = Second number
⇒ Therefore, the second number = 198

Example 2: The highest common factor and the lowest common multiple of two numbers are 825 and 25 respectively. If one of the two numbers is 275, find the other number.
Solution:

We know, LCM × HCF = Product of the Numbers (First number × Second number) then we get,
825 × 25 = 275 × Second number
825 × 25/ 275 = Second number
⇒ Therefore, the second number = 75

Example 3: Find the LCM and HCF of integers 26 and 91, verify that LCM x HCF = Product of the two numbers
Solution:

26 = 2 x 13
91 = 7 x 13
HCF = 13
LCM = 2 x 7 x 13 = 182
Product of two value 26 x 91 = 2366
Product of HCF and LCM 13 x 182 = 2366
⇒ Hence Proved, LCM × HCF = Product of the two Numbers

HCF of co-prime numbers is 1. Therefore LCM of given co-prime numbers is equal to the product of the numbers.
Example 1: Three numbers which are co-prime to each other are such that the product of the first two is 551 and that of the last two is 1073. The sum of the three numbers is:
Solution:

Since the numbers are co-prime, they contain only 1 as the common factor. Also, the given two products have the middle number in common.
So, middle number = H.C.F. of 551 and 1073 = 29;
First number = [latex]\frac{551}{29}[/latex] = 19;
Third number = [latex]\frac{1073}{29}[/latex] = 37.
∴ Required sum = (19 + 29 + 37) = 85.

Example 2: Take any two coprime numbers and find their product. Also find out if the product of their HCF and LCM is equal to product of the numbers.
Solution:

Well, consider a = 12 and b = 25. They are not prime but coprime (have no common dividers except 1).
a=[latex]2^{2}[/latex] x 3, b=[latex]5^{2}[/latex].
Their product is ab = 12 x 25 = 300. Their HCF is 1 as for any coprime numbers. Their LCM must include all their prime factors with their degrees, so LCM = [latex]2^{2}[/latex] x 3 x [latex]5^{2}[/latex]=300.
And yes, ab = HCF (a, b) x LCM (a, b) for these a and b.

Example 3: Find the HCF and LCM of 6, 72 and 120, using the prime factorization method.
Solution:

We have: 6 = 2 x 3,
72 = [latex]2^{3}[/latex] x [latex]3^{2}[/latex],
120 = [latex]2^{3}[/latex] x 3 x 5
Here, [latex]2^{1}[/latex] and [latex]3^{1}[/latex] are the smallest powers of the common factors 2 and 3 respectively.
So, HCF (6, 72, 120) = [latex]2^{1}[/latex] X [latex]3^{1}[/latex] = 2 X 3 = 6
[latex]2^{3}[/latex], [latex]3^{2}[/latex] and [latex]5^{1}[/latex] are the greatest powers of the prime factors 2, 3 and 5 respectively involved in the three numbers.
So, LCM (6, 72, 120) = [latex]2^{3}[/latex] x [latex]3^{2}[/latex] x [latex]5^{1}[/latex] = 360.

Example 1: A watch ticks 90 times in 95 seconds and another watch ticks 315 times in 323 seconds. If both the watches are started together, how many times will they tick together in the first hour?
Solution:

The first watch ticks every [latex]\frac{95}{90}[/latex] seconds.
They will tick together after (LCM. Of [latex]\frac{95}{90}[/latex] & [latex]\frac{323}{315}[/latex]) Seconds.
Now, LCM of [latex]\frac{95}{90}[/latex] and [latex]\frac{323}{315}[/latex] = [latex]\frac{LCM \: of \: 95, 323}{HCF \: of \: 90, 315}[/latex] = [latex]\frac{19 \times 5 \times 17}{45}[/latex]
The number of times they will tick in the first 3600 seconds = [latex]3600 \div \frac{19 \times 5 \times 17}{45}[/latex] = [latex]\frac{3600 \times 45}{19 \times 5 \times 17}[/latex] = 100 [latex]\frac{100}{323}[/latex]
Once they have already ticked in the beginning.
So in 1 hour they will tick 100 + 1 = 101 times.

Example 2: Find LCM and HCF of [latex]\frac{1}{2}[/latex], [latex]\frac{2}{3}[/latex] and [latex]\frac{3}{7}[/latex].
Solution:

We know, LCM of fractions = [latex]\frac{LCM \:of \:numerators}{HCF \:of \:denominators}[/latex]
LCM ([latex]\frac{1}{2}[/latex], [latex]\frac{2}{3}[/latex], [latex]\frac{3}{7}[/latex]) = [latex]\frac{LCM \:(1,\: 2,\: 3)}{HCF \:(2,\: 3,\: 7)}[/latex]
LCM (1, 2, 3) = 1 x 2 x 3 = 6
Now in order to find out HCF, use the prime factorization method i.e;
Here 2, 3 and 7 are prime numbers, so they are visible by "1" and itself only.
so, 2 = 2 x 1 3 = 3 x 1 7 = 7 x 1
In prime factorization method in case of HCF, we have to consider all the common factors with greatest index, in this case the common factor is "1"
So, HCF(2, 3, 7) = 1
∴ LCM of fractions = [latex]\frac{6}{1}[/latex] = 6
Now, Let's find out HCF of fraction
We know, HCF of fractions = [latex]\frac{HCF \:of \:numerators}{LCM \:of \:denominators}[/latex]
HCF ([latex]\frac{1}{2}[/latex], [latex]\frac{2}{3}[/latex], [latex]\frac{3}{7}[/latex]) = [latex]\frac{HCF \:(1,\: 2,\: 3)}{LCM \:(2,\: 3,\: 7)}[/latex]
As we know in order to find out HCF, use the prime factorization method i.e;
so, 1 = 1 x 1 2 = 2 x 1 3 = 3 x 1
In prime factorization method in case of HCF, we have to consider all the common factors with greatest index, in this case the common factor is "1"
So, HCF(1, 2, 3) = 1
Now let's find LCM(2, 3, 7) using divison method.
LCM(2, 3, 7) = 2 x 3 x 7 = 42.
∴ HCF of fractions = [latex]\frac{1}{42}[/latex]

Example 3: The H.C.F. of [latex]\frac{18}{35}[/latex], [latex]\frac{12}{25}[/latex], [latex]\frac{21}{40}[/latex], [latex]\frac{9}{10}[/latex]
Solution:

Here the required HCF is,
18 = 3 x 3 x 2
12 = 3 x 2 x 2
21 = 3 x 7
9 = 3 x 3
In prime factorization method in case of HCF, we have to consider all the common factors with greatest index, in this case the common factor is "3".
So, HCF(18, 12, 21, 9) = 3
Now let's find LCM of,
35 = 3 x 7
25 = 5 x 5
40 = 2 x 2 x 2 x 5
10 = 2 x 5
Highest factors of all these numbers is 2 x 2 x 2 x 5 x 5 x 7 = 1400.
∴ H.C.F. of [latex]\frac{18}{35}[/latex], [latex]\frac{12}{25}[/latex], [latex]\frac{21}{40}[/latex], [latex]\frac{9}{10}[/latex] = [latex]\frac{3}{1400}[/latex]

1. [latex]Product \ of \ two \ numbers[/latex] = [latex]Product \ of \ their \ H.C.F.\ and \ L.C.M[/latex]
2. [latex]Two \ numbers \ are \ said \ to \ be \ co-primes \ if \ their \ H.C.F. \ is \ 1[/latex]
3. [latex]H.C.F. = \frac{H.C.F. \ of \ numerators}{L.C.M \ of \ denominators}[/latex]
4. [latex]L.C.M. = \frac{L.C.M. \ of \ numerators}{H.C.F. \ of \ denominators}[/latex]

1.  Find the H.C.F. of 144, 288, 368 ?
Solution:

Given numbers are 144, 288, 368
First factorize the given numbers, i.e.
[latex] 144 = 2^4 × 3^2[/latex];
[latex]288 = 2^5 × 3^2[/latex];
[latex]368 = 2^5 × 3^2[/latex]
Therefore H.C.F. = [latex]2^4 × 3^2[/latex] = 144.

2. Reduce [latex] \frac{108}{360}[/latex] to lowest terms?
Solution:

Given fraction is [latex] \frac{108}{360}[/latex]
[latex]108 = 2^2 × 3^3[/latex]
[latex]360 = 2^3 × 3^2 × 5[/latex]
H.C.F. of 108 and 360 is [latex]2^2 × 3^2[/latex] = 36
Now, By dividing the numerator and denominator by 36,
⇒[latex]\frac{108}{360} = \frac{108}{360} × \frac{360}{360}[/latex]
⇒[latex]\frac{3}{10}[/latex]
Therefore [latex]\frac{108}{360} = \frac{3}{10}[/latex]

3. The H.C.F. of two numbers is 42 and their L.C.M. is 1260. If one of the numbers is 210, find the other?
Solution:

Given that
H.C.F. of two numbers = 42
L.C.M. of two numbers = 1260
One of the number = 210
[latex]Other number = \frac{ H.C.F. of two numbers × L.C.M. of two numbers}{one of the number}[/latex]
substitute the given values in the above fromula,
[latex]Other number = \frac{42 × 1260}{210}[/latex] = 252
Hence, other number = 252.

4. Find the least number which when divided by 35, 45, 55, leaves remainders 18, 28, 38 respectively?
Solution:

Here the difference between any divisor and the corresponding remainder is 17 i.e.
(35 - 18) = 17
(45 - 28) = 17
(55 - 38) = 17
Therefore Required number = (L.C.M. of 35,45,55) -17
L.c.m of 35, 45, 55 is 3465
⇒ Required number = 3465 - 17 = 3448
Hence, least number = 3448.

5. If the ratio of two numbers is 13 : 15 and their L.C.M. is 39780. Then the numbers are?
Solution:

Given that
Ratio of two numbers = 13 : 15
Their L.C.M. is 39780
Assume the two numbers as [latex]13x and 15x [/latex]
Now 13[latex]x × 15x [/latex] = 39780
⇒[latex] x [/latex] × 195 = 39780
⇒[latex] x = \frac{39780}{195}[/latex]
⇒[latex] x [/latex]= 204
Therefore, substitute the value of [latex] x [/latex] i.e.
13 x [latex] x [/latex] = 13 x 204 = 2652
15 x [latex] x [/latex] = 15 x 204 = 3060
Hence, the two numbers are 2652 and 3060.