Introduction
Introduction
In arithmetic, the traditional name for the geometry of three-dimensional Euclidean space is solid geometry. Solid geometry deals with the measurement of different strong figures or Polyhedrons (three-dimensional figures) including cuboids, cubes, cylinders, spheres, pyramids & cones and also with the estimation of volumes of them.
A figure that has depth in addition to width and height is a space figure or three dimensional figures. A tennis ball, a box, a bicycle and a redwood tree are all everyday examples of space figures.
Having all flat faces in a three-dimensional figure is known as a polyhedron. Cuboids and cube belong to polyhedrons whereas sphere, cylinder and cone are not polyhedrons.
Quantitative Aptitude -BANKING|SSC|RAILWAYS|INSURANCE|RECRUITMENT EXAMS - EBOOKS
 Methods
Methods
Measurement terms:
Cross-Section:
A cross-section is the shape of a particular two-dimensional "slice" of a space figure.
Eg: By the cross-section of the cylinder, a circle is formed.
Volume:
- Measure of how much three-dimensional figure takes-up is known as volume.
- Just as area is used to measure a plane figure, volume is used to measure a space figure.
- Adjacent faces are perpendicular to each other.
- Each line segment that is the intersection of two faces is called an edge.
- Vertex is each point at which the edges intersect.
- 12 edges and 8 vertices are there.
 Formula
Formula
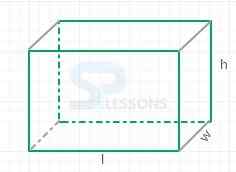
- 1. Volume of cuboid = l x w x h
2. Surface area of cuboid = 2lw + 2lh + 2wh
3. Diagonal length of a cuboid = [latex]\sqrt{(l^2 + w^2 + h^2)}[/latex]
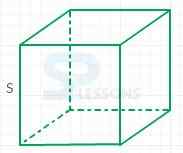
4. Volume of a cube = [latex]S^3[/latex]
5. Surface area of a cube = 6[latex]S^2[/latex]
6. Diagonal length of a cube = S[latex]\sqrt{3}[/latex]
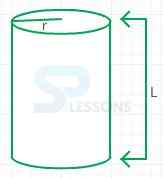
7. Volume of a cylinder = π[latex]r^2[/latex]h
8. Surface area of a cylinder = 2πrh + 2π[latex]r^2[/latex]
9. Volume of the sphere = π[latex]\frac{4}{3}r^3[/latex]cubic units
10. Surface area of the sphere = 4π[latex]r^2[/latex]
 Samples
Samples
1. A cube and a rectangular solid are equal in volume. Find the length of an edge of the cube, if the length of the edges of the rectangular solid are 4, 8 and 16?
Solution:
A. The quantity on the left is greater.
B. The quantity on the right is greater.
C. Both are equal.
D. The relationship cannot be determined without further information.
Solution:
A. The quantity on the left is greater.
B. The quantity on the right is greater.
C. Both are equal.
D. The relationship cannot be determined without further information.
Solution:
A. The quantity on the left is greater.
B. The quantity on the right is greater.
C. Both are equal.
D. The relationship cannot be determined without further information.
Solution:
- Given that,
All the dimensions to calculate the volume of the rectangular solid, which is 4, 8 and 16.
This is also the volume of the cube.
Therefore, the length of an edge of the cube is the cubic root of (16 x 8 x 4) = 8.
- Given that,
Radius = 20 feet
Depth = 50 feet
Volume of the cylindrical building (V) = π[latex]r^2[/latex]h
V = π[latex](20)^2[/latex] x 50
V = 20000π
Therefore, the volume of the building is 20000π cubic feet.
| Quantity A | Quantity B |
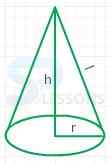
| The volume of the cone | 300[latex]{cm}^3[/latex] |
- Given that,
Radius = 5 cm
height = 10 cm
Now, volume of the cone (V) = π[latex]\frac{1}{3}r^2[/latex]h
V = π[latex]\frac{1}{3}5^2[/latex] x 10
V = (250π)[latex]\frac{1}{3}[/latex]
V = 261.67[latex]{cm}^3[/latex]
Hence, option (B) is correct answer.
| Quantity A | Quantity B |
| The surface area of the sphere | 452.16 sq.cm |
- Given that,
Radius of a sphere is 6cm.
Now, Surface area of sphere (S) = 4π[latex]r^2[/latex]
S = 4 x 3.14 [latex]6^2[/latex]
S = 12.56 x 36
S = 452.16 sq.cm
Thus, the two values are equal.
Therefore, correct option is (C).
| Quantity A | Quantity B |
| The volume of a cylinder if the radius is doubled | The volume of a cylinder if the height is doubled |
- The volume of the cylinder multiplies the square of the radius by the height.
Doubling the radius of a cylinder will change the volume more fundamentally because of squaring involved.
Hence, option (A) is right answer.