Estimation of functions:
Function estimation means calculating [latex]f(x)[/latex] at some particular value [latex]x[/latex].
Eg: [latex]f(x)[/latex] = [latex]x^2[/latex] - 1. Then find [latex]f(2)[/latex]?
Substitute [latex]x[/latex] = 2, then
[latex]f(2)[/latex] = [latex]2^2[/latex] - 1
[latex]f(2)[/latex] = 3
Operations on functions:
Functions can be added, subtracted, multiplied and divided like any other quantity. Some of the below listed key rules will make these operations simpler.
Rules:
For any two functions of [latex]f(x)[/latex] and [latex]g(x)[/latex]
Addition: [latex](f + g)(x)[/latex] = [latex]f(x)[/latex] + [latex]g(x)[/latex]
Subtraction: [latex](f - g)(x)[/latex] = [latex]f(x)[/latex] - [latex]g(x)[/latex]
Multiplication: [latex](f * g)(x)[/latex] = [latex]f(x)[/latex] * [latex]g(x)[/latex]
Division: [latex]\frac{f}{g}(x)[/latex] = [latex]\frac{f(x)}{g(x)}[/latex]; [latex]g(x)[/latex] ≠ 0
Compound function:
A function that performs on another function is known as a compound function.
It is represented as "[latex]f(g(x))[/latex]".
First evaluate internal function [latex]g(x)[/latex] then outer function [latex]f(x)[/latex]. It's double substitution.
Domain and range:
Domain of functions: The set of inputs([latex]x[/latex] values) for which the function is defined is defined as a domain of a function.
How to find domain of a function:
First look for any restrictions on the domain, to calculate the domain of the function. There are two main restrictions for function domain. They are:

• Division by zero: It is impossible mathematically. Eg: [latex]f(x)[/latex] = [latex]\frac{1}{x - 2}[/latex] is undefined at [latex]x[/latex] = 2, since when [latex]x[/latex] = 2, the function [latex]f(x)[/latex] = [latex]\frac{1}{0}[/latex]. Therefore, a function is therefore undefined for all the values of [latex]x[/latex] for which division by zero occurs.


• Negative numbers under square roots: The square roots of a negative number does not exist, so if a function contains a square root, such [latex]f(x)[/latex] = [latex]\sqrt{x}[/latex], the domain must be [latex]x[/latex] > 0.

Range of a function: The set of all values of [latex]f(x)[/latex] that can be generated by the function is known as a range.

• The easiest way to find range is to visualize it on a graph.


• [latex]x[/latex]-axis consists of all the values of [latex]x[/latex] of domain.


• [latex]y[/latex]-axis consists of all the values of [latex]f(x)[/latex] of range.

There are two main signs of functions with limited ranges. They are absolute value and even exponents.
Absolute value: The absolute value of a quantity is always positive.
Eg: If [latex]f(x)[/latex] = [latex]\mid{x}\mid[/latex]
[latex]f(x)[/latex] must be always positive.
So, the range includes only zero and positive numbers i.e. range is [latex]f(x)[/latex] ≥ 0.
Never expect that any function with an absolute value symbol has the same range.
The range of [latex]g(x)[/latex] = [latex]\mid{x}\mid[/latex] is zero and all the negative quantity will be positive i.e. [latex]f(x)[/latex] ≤ 0.
Even exponents: By squaring a number (or raise it to any multiple of 2) at any time the resulting quantity will be positive.
How to find range of a function:
Figure A

Figure B

• It is similar to finding of domain.


• First, look for absolute values, even exponents or other reasons that the range would be restricted.


• Adjust the range step by step to find the domain.

Quadratic function:

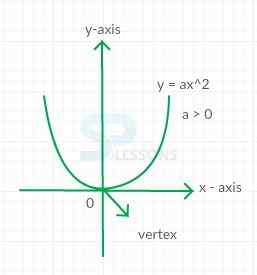
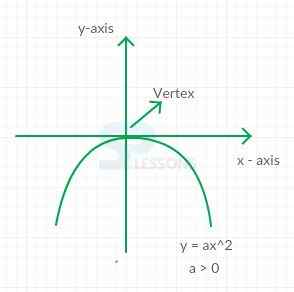
• The graphs of equations of the form [latex]y[/latex] = [latex]ax^2[/latex] are examples of parabola.


• These parabolas are symmetric about the [latex]y[/latex] axis; the open upward and have a lowest point at (0, 0) if [latex]a[/latex] > 0 in (figure A) and the open downward have a highest point at (0, 0) if a < 0 (figure B).


• The highest or lowest point of the graph of [latex]y[/latex] = [latex]ax^2[/latex] is called the vertex of the parabola and its line of symmetry is known as the axis of symmetry as simply the axis of the parabola.

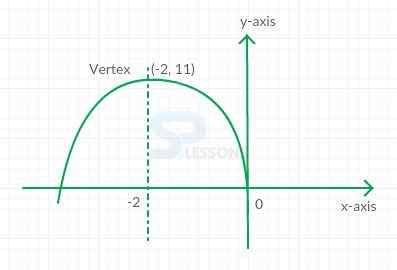
1. Find the vertex and axis of symmetry of the graph of [latex]f(x)[/latex] = -3[latex]x^2[/latex] - 12[latex]x[/latex] - 1 and sketch the graph.
Solution:

Given
[latex]f(x)[/latex] = -3[latex]x^2[/latex] - 12[latex]x[/latex] - 1
Consider the vertex formula with [latex]a[/latex] = -3 and b = -12
[latex]h[/latex] = [latex]\frac{-b}{2a}[/latex]
= [latex]\frac{-12}{2(-3)}[/latex]
= -2
[latex]k[/latex] = [latex]f(h)[/latex] = [latex]f(-2)[/latex]
= -3[latex](-2)^2[/latex] - 12(-2) - 1
= 11
Therefore, the graph is as shown below:



It is a parabola, opening downward, with vertex as [latex]x[/latex] = -2.

2. Find the vertex and the [latex]y[/latex] and [latex]x[/latex] intercepts of the graph of [latex]f(x)[/latex] = [latex]-2x^2 - 5x + 3[/latex]. Determine whether the graph open upward or downward and sketch the graph?
Solution:

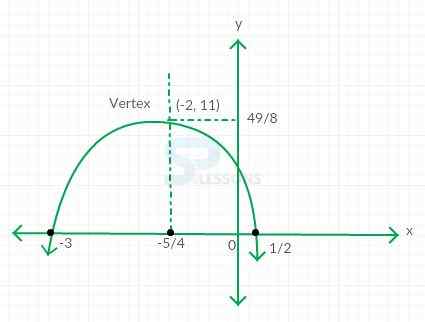
Given
[latex]f(x)[/latex] = [latex]-2x^2 - 5x + 3[/latex]
Here, [latex]a[/latex] = -2, [latex]b[/latex] = -5, and [latex]c[/latex] = 3
By vertex formula [latex]h[/latex] = [latex]\frac{-b}{2a}[/latex]
= [latex]\frac{-(-5)}{2(-2)}[/latex]
= [latex]\frac{-5}{4}[/latex]
[latex]k[/latex] = [latex]f(h)[/latex] = [latex]f(\frac{-5}{4})[/latex]
= -2[latex](\frac{-5}{4})^2[/latex] - 5[latex]\frac{-5}{4}[/latex] + 3
= [latex]\frac{49}{8}[/latex]
The [latex]y[/latex] intercept is [latex]c[/latex] = 3
The [latex]x[/latex] intercept are solutions of equation i.e.
-2[latex]x^2[/latex] - 5[latex]x[/latex] + 3 = 0
= ([latex]x[/latex] + 3)(-2[latex]x[/latex] + 1) = 0
[latex]x[/latex] = -3 and [latex]\frac{1}{2}[/latex]
As [latex]a[/latex] = -2 < 0, the graph opens downward as shown below.

3. If [latex]\frac{3x}{4 - x}[/latex], find the value of [latex]f(x + 1)[/latex]?
Solution:

Given that,
[latex]f(x)[/latex] = [latex]\frac{3x}{4 - x}[/latex]
Now, substitute [latex](x + 1)[/latex] in the place of [latex]x[/latex] i.e.
[latex]f(x + 1)[/latex] = [latex]\frac{3(x + 1)}{4 - (x + 1)}[/latex]
[latex]f(x + 1)[/latex] = [latex]\frac{3x + 3}{4 - x - 1}[/latex]
[latex]f(x + 1)[/latex] = [latex]\frac{3x + 3}{3 - x}[/latex]
Therefore, the value of [latex]f(x + 1)[/latex] = [latex]\frac{3x + 3}{3 - x}[/latex]

4. A. Find the value of [latex]f(5)[/latex], if [latex]f(x)[/latex] = [latex]x^2[/latex] - 3.
B. If [latex]f(x)[/latex] = [latex]x[/latex] and [latex]g(x)[/latex] = [latex]x^2[/latex], then find the value of [latex]\frac{f}{g}(x)[/latex]?
Solution:

A. Given that,
[latex]f(x)[/latex] = [latex]x^2[/latex] - 3
Now, substitute 5 in the place of [latex]x[/latex] i.e.
[latex]f(5)[/latex] = [latex]5^2[/latex] - 3
[latex]f(5)[/latex] = 22
B. Given that,
[latex]f(x)[/latex] = [latex]x[/latex]
[latex]g(x)[/latex] = [latex]x^2[/latex]
Now, [latex]\frac{f}{g}(x)[/latex] = [latex]\frac{f(x)}{g(x)}[/latex] where [latex]g(x)[/latex] ≠ 0.
[latex]\frac{f}{g}(x)[/latex] = [latex]\frac{x}{x^2}[/latex]
[latex]\frac{f}{g}(x)[/latex] = [latex]\frac{1}{x}[/latex]

5. A. If [latex]h(x)[/latex] = [latex]x^2 + 2x[/latex] and [latex]j(x)[/latex] = [latex]\mid\frac{x}{4} + 2\mid[/latex], then find the value of [latex]j(h(x))[/latex]?
B. If [latex]f(x)[/latex] = [latex]3x + 1[/latex] and [latex]g(x)[/latex] = [latex]\sqrt{5x}[/latex]. What is [latex]g(f(x))[/latex]?
Solution:

A. Given that,
[latex]h(x)[/latex] = [latex]x^2 + 2x[/latex]
[latex]j(x)[/latex] = [latex]\mid\frac{x}{4} + 2\mid[/latex]
Initially consider [latex]h(x)[/latex] = [latex]x^2 + 2x[/latex]
Substitute 4 in the place of [latex]x[/latex] i.e.
[latex]h(4)[/latex] = [latex]4^2 + 2(4)[/latex]
[latex]h(4)[/latex] = 24
Now, [latex]j(h(x))[/latex] = [latex]j(24)[/latex]
So, substitute 24 in the place of x in [latex]j(x)[/latex] = [latex]\mid\frac{x}{4} + 2\mid[/latex]
[latex]j(24)[/latex] = [latex]\mid\frac{24}{4} + 2\mid[/latex]
[latex]j(24)[/latex] = [latex]\mid6 + 2\mid[/latex]
[latex]j(24)[/latex] = 8
Therefore, [latex]j(h(x))[/latex] = [latex]j(24)[/latex] = 8.
B. Given that,
[latex]f(x)[/latex] = [latex]3x + 1[/latex]
[latex]g(x)[/latex] = [latex]\sqrt{5x}[/latex]
Now, [latex]g(f(x))[/latex] = [latex]g(3x + 1)[/latex]
So, substitute [latex]3x + 1[/latex] in the place of [latex]x[/latex] in [latex]g(x)[/latex] = [latex]\sqrt{5x}[/latex] i.e.
[latex]g(f(x))[/latex] = [latex]\sqrt{5(3x + 1)}[/latex]
[latex]g(f(x))[/latex] = [latex]\sqrt{15x + 5}[/latex]
Therefore, [latex]g(f(x))[/latex] = [latex]\sqrt{15x + 5}[/latex].