Introduction
Introduction
Mensuration Problems deals with the area, perimeter, diagonal, height, circumference etc. of figures like square, rectangle, parallelogram, rhombus, trapezium, triangle, equilateral triangle, cube, cuboid, cylinder, cone, sphere, hemi-sphere, prism, circle, semi circle, sector.
- Mensuration: It is a branch of mathematics which deals with the lengths of lines, areas of surfaces and volumes of solids.
Plane Mensuration: It deals with the sides, perimeters and areas of plane figures of different shapes.
Solid Mensuration: It deals with the areas and volumes of solid objects
Quantitative Aptitude -BANKING|SSC|RAILWAYS|INSURANCE|RECRUITMENT EXAMS - EBOOKS
 Methods
Methods
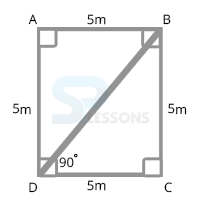
Square: It is a regular quadrilateral which consists four equal sides and four equal angles. Every angle is 90 degrees.
-
Here AB = BC = CD = AD = 5 m = a (Let)
1. Perimeter of square = 4 x sides = 4a
= 4 x 5 = 20m
2. Area of a square = [latex](sides)^{2}[/latex]
= [latex]a^{2}[/latex] = [latex](5)^{2}[/latex] = 25 sq. m
3. Side of a square = [latex]\sqrt{area}[/latex] = [latex]\sqrt{25}[/latex] = 5m or,
[latex]\frac{Perimeter}{4}[/latex] = [latex]\frac{20}{4}[/latex] = 5m
4. Diagonal of a square = [latex]\sqrt{2}[/latex] x side = [latex]\sqrt{2}[/latex] a
= [latex]\sqrt{2}[/latex] x 5 = 5[latex]\sqrt{2}[/latex] m
5. Side of a square = [latex] \frac{diagonal}{\sqrt{2}}[/latex] = [latex]\frac{5\sqrt{2}}{\sqrt{2}}[/latex] = 5m
-
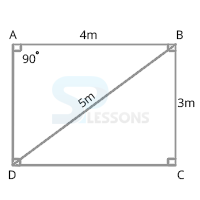
Here AB = CD; length l = 4m
AD = BC; breadth b = 3m
1. Perimeter of a rectangle = 2(length + breadth)
= 2(l + b)
= 2(4 + 3) = 14 m
2. Area of rectangle = length x breadth = l x b = 4 x 3
= 12 [latex]m^{2}[/latex]
3. Length of a rectangle : [latex]\frac{area}{breadth}[/latex] = [latex]\frac{A}{b}[/latex] = [latex]\frac{12}{3}[/latex] = 4 m
Or, [[latex]\frac{perimeter}{2}[/latex] - breadth] = ([latex]\frac{14}{2}[/latex] – 3) = 4m
Breath of a rectangle : [latex]\frac{area}{length}[/latex] = [latex]\frac{A}{l}[/latex] = [latex]\frac{12}{4}[/latex] = 3 m
Or, [[latex]\frac{perimeter}{2}[/latex] - length] = ([latex]\frac{14}{2}[/latex] - 4) = 3 m
-
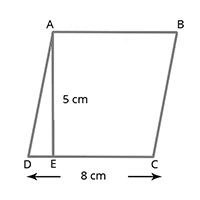
(i) Area of parallelogram = base x height
= b x h
= 8 x 5 = 40 sq.cm.
(ii) Perimeter of a parallelogram = 2(AB + BC)
= 2( 8 + 5 ) = 26 cm
-
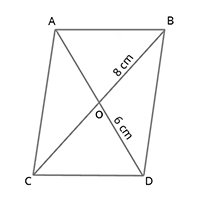
i) Area of rhombus = [latex]\frac{1}{2}[/latex] x (product of diagonals)
= [latex]\frac{1}{2} (d_{1} . d_{2}) [/latex] = [latex]\frac{1}{2}[/latex] x 8 x 6 = 24[latex]cm^{2}[/latex]
ii) Perimeter of rhombus = 4 x side = 4a
here AB = BC = CD = AD = 4a
AC = [latex]d_{1}[/latex], BD = [latex]d_{2}[/latex]
-
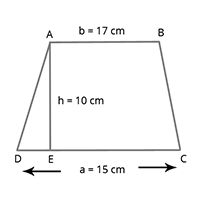
Area if a trapezium = [latex]\frac{1}{2}[/latex] x ( sum of parallel sides ) x height
= [latex]\frac{1}{2}[/latex] x ( a + b ) x h
= [latex]\frac{1}{2}[/latex] x (15 + 17) x 10
= [latex]\frac{1}{2}[/latex] x 32 x 10 = 160 [latex]cm^{2}[/latex]
-
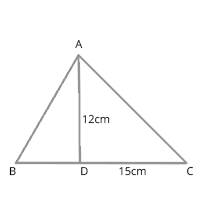
1. Area of triangle = [latex]\frac{1}{2}[/latex] x base x height
= [latex]\frac{1}{2}[/latex] x 15 x 12 = 90 sq. cm
here AD = 12 cm = height, BC = 15 cm = base
2. Semi perimeter of a triangle
S = [latex]\frac{a + b + c}{2}[/latex] = [latex]\frac{10 + 8 + 6}{2}[/latex] = 12 cm
here BC = a, AC = b, AB = c
3. Area of triangle = [latex]\sqrt{s(s – a)(s – b)(s – c)}[/latex]
Where a = 10cm, b = 8cm, c = 6cm, s = 12cm
= [latex]\sqrt{12(12 - 10)(12 - 8)(12 - 6)}[/latex]
= [latex]\sqrt{12 \times 2 \times 4 \times 6}[/latex]
= 24 [latex]cm^{2}[/latex]
4. Perimeter of a triangle = 2s = (a + b + c)
= 10 + 8 + 6 = 24 cm
-
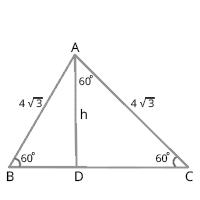
1. Area of an equilateral triangle = [latex]\frac{\sqrt{3}}{4}[/latex] x [latex](side)^{2}[/latex]
= [latex]\frac{\sqrt{3}}{4}[/latex] x [latex](4\sqrt{3})^{2}[/latex]
= [latex]\frac{\sqrt{3}}{4}[/latex] x 48 = [latex]12\sqrt{3}[/latex] [latex]cm^{2}[/latex]
2. Height of an equilateral triangle = [latex]\frac{\sqrt{3}}{2}[/latex] x [latex](side)^{2}[/latex]
= [latex]\frac{\sqrt{3}}{2}[/latex] x [latex]4\sqrt{3}[/latex]
= 6cm
3. Perimeter of an equilateral triangle = 3 x (side)
= 3 x [latex]4\sqrt{3}[/latex] = [latex]12\sqrt{3}[/latex] cm
-
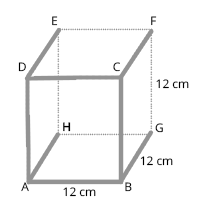
1. Volume of cube = [latex](side)^{3}[/latex]
= [latex]12^{3}[/latex]
= 1728 cubic cm
Cube: All sides are equal = 12 cm
2. Side of a cube = [latex]\sqrt[3]{Volume}[/latex]
= [latex]\sqrt[3]{1728}[/latex]
= 12 cm
3. Diagonal of cube = [latex]\sqrt{3}[/latex] x (Side) = [latex]\sqrt{3}[/latex] x 12 = 12 [latex]\sqrt{3}[/latex] cm
4. Total surface area of a cube = 6 x [latex](Side)^{2}[/latex] = 6 x [latex](12)^{2}[/latex] = 864 sq.cm
-
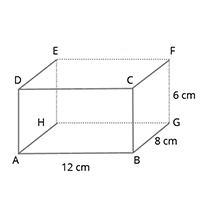
1. Total surface area of cuboid = 2 (lb + bh + hl) sq. unit
Here l = length, b = breadth, h = height
= 2(12 x 8 + 8 x 6 + 6 x 12)
= 2(96 + 48 + 72) = 2 x 216 = 432 sq. cm.
2. Volume of a cuboid = (length × breadth × height) = lbh
= 12 × 8 × 6 = 576 cuboic cm
3. Diagonal of a cuboid = [latex]\sqrt{l^{2} + b^{2} + h^{2}}[/latex] = [latex]\sqrt{12^{2} + 8^{2} + 6^{2}}[/latex]
= [latex]\sqrt{144 + 64 + 36}[/latex] = [latex]\sqrt{244}[/latex] = [latex]2\sqrt{61}[/latex] cm.
4. Length of cuboid = [latex]\frac{Volume}{Breadth \times Height}[/latex] = [latex]\frac{v}{b \times h}[/latex]
5. Breadth of cuboid = [latex]\frac{Volume}{Length \times Height}[/latex] = [latex]\frac{v}{l \times h}[/latex]
6. Height of cuboid = [latex]\frac{Volume}{length \times breadth}[/latex] = [latex]\frac{v}{l \times b}[/latex]
-
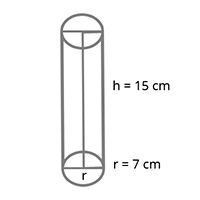
1. Area of curved surface = (perimeter of base) x height
= [latex]2 \pi r h [/latex] sq. unit
= 2 x [latex]\frac{22}{7}[/latex] x 7 x 15 = 660 sq. cm
2. Total surface area = area of circular ends + curved surface area
= [latex]2 \pi r^{2}[/latex] + [latex]2 \pi r(r + h) [/latex] sq. unit
= 2 x [latex]\frac{22}{7}[/latex] x 7(15 + 7)
= 2 x 22 x 22
= 968 sq. cm.
3. Volume = (area of base) x height
= [latex](\pi r^{2})[/latex] x h = [latex]\pi r^{2}h[/latex]
= [latex]\frac{22}{7}[/latex] x 7 x 7 x 15 = 2310 cubic cm.
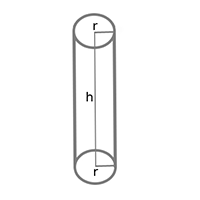
4. Volume of a hollow cylinder = [latex]\pi R^{2}h - \pi r^{2}h[/latex]
= ([latex]\pi h (R^{2} - r^{2})[/latex]) = [latex] \pi h(R + r)(R - r)[/latex]
= [latex] \pi \times height \times (sum of radii)(difference of radii)[/latex]
Here R, r are outer and inner radii respectively and h is the height.
-
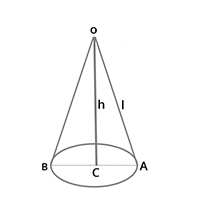
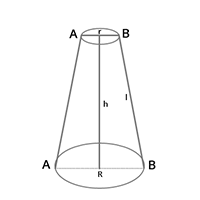
1. In right angled [latex ]\bigtriangleup[/latex] OAC, we have
[latex]l^{2}[/latex] = [latex]h^{2}[/latex] + [latex]r^{2}[/latex]
(Here r = 35 cm, l = 37 cm, h = 12 cm)
Or, l = [latex]\sqrt{h^{2} + r^{2}}[/latex]
h = [latex]\sqrt{l^{2} – r^{2}}[/latex], r = [latex]\sqrt{l^{2} – h^{2}}[/latex]
Where l = slant height, h = height, r = radius of base
2. Curved surface area = [latex]\frac{1}{2}[/latex] x (perimeter of base) x slant height
= [latex]\frac{1}{2}[/latex] x [latex]2 \pi r[/latex] x l = [latex]\pi r l[/latex] sq. unit
= [latex]\frac{22}{7}[/latex] x 35 x 37 = 4070 sq. cm
3. Total surface area S = area of circular base + curved surface area = [latex](\pi r^{2} + \pi r l)[/latex] = [latex]\pi r (r + l)[/latex] sq. unit
= [latex]\frac{22}{7}[/latex] x 35 (37 + 35) = 7920 sq. cm
4. Volume of cone = [latex]\frac{1}{3}[/latex] (area of base) x height
= [latex]\frac{1}{3} (\pi r^{2})[/latex] x h = [latex]\frac{1}{3} \pi r^{2} h[/latex] cubic unit
= [latex]\frac{1}{3}[/latex] x [latex]\frac{22}{7}[/latex] x 35 x 35 x 12
= 15400 cubic cm
Frustum of Cone:
5. Volume of frustum = [latex]\frac{1}{3} \pi h (R^{2} + r^{2} + Rr)[/latex] cubic unit
6. Lateral surface = [latex]\pi l (R + r)[/latex]
Where [latex]l^{2}[/latex] = [latex]h^{2}[/latex] + [latex](R - r)^{2}[/latex]
7. Total surface area = [latex]\pi [R^{2} + r^{2} + l(R + r)][/latex]
R, r be the radius of base and top the frustum
ABB ‘A’ h and l be the vertical height and slant
Height respectively.
-
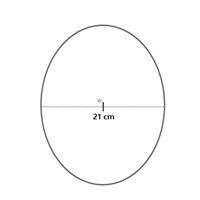
1. Surface area = [latex]4 \pi r^{2}[/latex]
= 4 x [latex]\frac{22}{7}[/latex] x [latex](10.5)^{2}[/latex] = 1386 sq. cm
Here, d = 21 cm
Therefore, r = 10.5 cm
2. Radius of sphere = [latex]\sqrt{ \frac{surface area}{4 \pi}}[/latex] = [latex]\sqrt{ \frac{1386 \times 7}{4 \times 22}}[/latex] = 10.5 cm
3. Diameter of sphere = [latex]\sqrt{ \frac{surface}{4 \pi}}[/latex] = [latex]\sqrt{ \frac{surface}{4 \pi}}[/latex] = [latex]\sqrt{ \frac{1386 /times 7}{22}}[/latex] = 21 cm
4. Volume of sphere V = [latex]\frac{4}{3} \pi r^{3}[/latex] = [latex]\frac{4}{3} \pi (\frac{d}{2})^{3}[/latex] = [latex]\frac{1}{6} \pi d^{3}[/latex]
= [latex]\frac{1}{6}[/latex] x [latex]\frac{22}{7}[/latex] x 21 x 21 x 21 = 4831 cubic cm
5. Radius of sphere = [latex]\sqrt{ \frac{3}{4 \pi} \times volume of shpere}[/latex]
6. Diameter = [latex]\sqrt[3]{ \frac{6 \times v}{\pi}}[/latex]
7. Volume of spherical ring = [latex]\frac{4}{3} \pi (R^{3} – r^{3}[/latex]
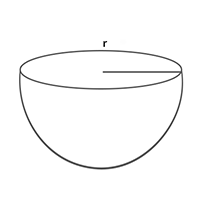
Hemisphere: In geometry, hemisphere is an exact half of sphere.
8. Curved surface of hemisphere = 2 [latex]\pi r^{2}[/latex]
9. Volume of hemisphere = [latex]\frac{2}{3} \pi r^{3}[/latex]
10. Total surface area of hemisphere = [latex]3 \pi r^{2}[/latex]
Note:
V = volume, A = area, h = height, b = base,breadth, d= diameter, R = outer radius, r = inner radius,
[latex]\pi[/latex] = [latex]\frac{22}{7}[/latex] = 3.142, a = side.
-
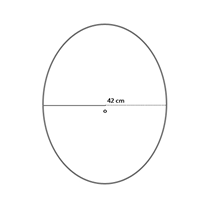
1. Circumference of a circle = [latex]\pi[/latex] x diameter
= [latex]\pi[/latex] x [latex]2r[/latex] = [latex]2 \pi r[/latex]
= 2 x [latex]\frac{22}{7}[/latex] x 42 = 264 cm
2. Radius of a circle = [latex]\frac{circumference}{2 \pi}[/latex] = [latex]\frac{264 \times 7}{2 \times 22}[/latex] = 42 cm
3. Area of a circle = [latex]\pi \times r^{2}[/latex] = [latex]\frac{22}{7}[/latex] x [latex]42^{2}[/latex] = [latex]\frac{22}{7}[/latex] x 42 x 42 = 5544 [latex]cm^{2}[/latex]
4. Radius of a circle = [latex]\sqrt{\frac{area}{\pi}}[/latex]
= [latex]\sqrt{\frac{5544}{22} \times 7}[/latex] = [latex]\sqrt{1764}[/latex] = 42cm
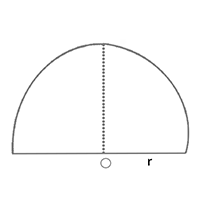
Semi-circle: It is a two-dimensional geometric shape that also includes the diameter segment from one end of the arc to the other as well as all the interior points.
5. Area of a semi circle = [latex]\frac{1}{2} \pi r^{2}[/latex] = [latex]\frac{1}{8} \pi d^{2}[/latex]
= [latex]\frac{1}{2}[/latex] x [latex]\frac{22}{7}[/latex] x [latex]42^{2}[/latex] = [latex]2772 cm^{2}[/latex]
6. Circumference of semi circle = [latex]\frac{22}{7}[/latex] x 42 = 132 cm
7. Perimeter of semi circle = [latex](\pi r + 2r)[/latex] = [latex](\pi + 2)r[/latex] = [latex](\pi + 2)\frac{d}{2}[/latex]
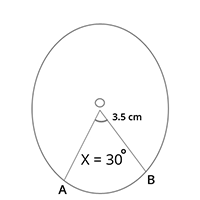
8. Area of sector OAB = [latex]\frac{x}{360}[/latex] x [latex]\pi r^{2}[/latex]
(x being the central angle)
= [latex]\frac{30^{0}}{360^{0}}[/latex] x [latex]\frac{22}{7}[/latex] x 3.5 x 3.5 = 3.21 sq. m.
9. Central angle by arc AB = [latex]360^{0}[/latex] x [latex]\frac{area of OAB}{are of circle}[/latex]
= [latex]360^{0}[/latex] x [latex]\frac{3.21}{\frac{22}{7} \times 3.5 x 3.5}[/latex] = [latex]\frac{360 \times 321}{22 \times 35 \times 5}[/latex] = [latex]30^{0}[/latex](approx)
10. Radius of circle = [latex]\sqrt{\frac{360^{0}}{central \ angle \ by \ arc} \times \frac{area \ of \ OAB}{\pi}}[/latex]
= [latex]\sqrt{\frac{360^{0}}{30^{0}} \times \frac{3.21}{\frac{22}{7}}}[/latex] = [latex]\sqrt{\frac{134.82}{11}}[/latex] = [latex]\sqrt{12.23}[/latex] = 3.5 m.
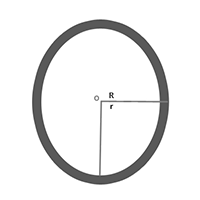
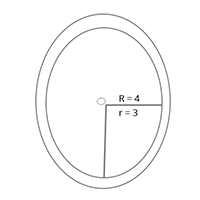
11. Area of ring = difference of the area of two circle
= [latex]\pi R^{2}[/latex] - [latex]\pi r^{2}[/latex] = ([latex]R^{2} - r^{2}[/latex])
= [latex]\pi[/latex](R + r)(R - r)
= (sum of radius)(diff. of radius)
= [latex]\frac{22}{7}[/latex] x (4 + 3)(4 - 3) = [latex]\frac{22}{7}[/latex] x 7 x 1
= 22 sq. cm.
 Formulae
Formulae
1. Square:
Area = [latex](side)^2[/latex]
Perimeter = 4 x side
Diagonal = [latex]\sqrt{2(side)^2}[/latex]
2. Rectangle:
Area = Length x Breadth
Perimeter = 2(Length x Breadth)
Diagonal = [latex]\sqrt{l^2 + b^2}[/latex]
3. Parallelogram:
Area = Base x Height
Perimeter = 2(Length x Breadth)
Base = [latex]\frac{Area}{Height}[/latex]
4. Rhombus:
Area = [latex]\frac{1}{2}* d_{1} d_{2}[/latex]
Where, [latex]d_{1} \ and \ d_{2}[/latex] are diagonals.
Perimeter = 4 x side
Diagonal = [latex]\frac{2 * area}{other diagonal}[/latex]
5. Trapezium:
Area = [latex]\frac{1}{2}(a + b) * h[/latex]
Perimeter = Sum of the sides
6. Triangle:
Area = [latex]\frac{1}{2} * Base * Height[/latex] (or) [latex]\sqrt{s(s - a)(s - b)(s - c)}[/latex]
Where a, b, c are sides of triangle and s = [latex]\frac{a + b + c}{2}[/latex]
Perimeter = Sum of the sides
7. Equilateral Triangle:
Area = [latex]\frac{\sqrt{3}}{2}(side)^2[/latex]
Perimeter = 3(Side)
8. Cube:
Let each edge of a cube be of length [latex]a[/latex]. Then,
Volume = [latex]a^3[/latex] cubic units
Surface area = 6[latex]a^2[/latex] sq. units
Diagonal = [latex]\sqrt{3}a[/latex]units
9. Cuboid:
Let l - length, b - breadth, h - height. Then,
Volume = (l x b x h) cubic units
Surface area = 2(lb + bh + lh) sq. units
Diagonal = [latex]\sqrt{l^2 + b^2 + h^2}[/latex] units
10. Cylinder:
Let radius of base = r and height( or length) = h. Then,
Volume = [latex]\pi r^2 h [/latex] cubic units
Curved Surface area = 2[latex]\pi r h[/latex] sq. units
Total surface area = 2([latex]\pi rh + 2\pi r^2[/latex]) = 2[latex]\pi r(h + r)[/latex]sq. units
11. Cone:
Let radius of base = r and height = h. Then,
Slant height, l = [latex]\sqrt{h^2 + r^2}[/latex] units
Volume = [latex]\frac{1}{3}\pi r^2 h[/latex] cubic units
Curved surface area = [latex]\pi r l[/latex] sq. units
Total surface area = [latex]\pi r l + \pi r^2[/latex] sq. units
12. Sphere:
Let radius of the sphere be r. Then,
Volume = ([latex]\frac{4}{3} \pi r^3[/latex]) cubic units
Surface area = [latex]\pi r^2[/latex] sq. units
13. Hemisphere:
Let the radius of a hemisphere be [latex]r[/latex].
Volume = [latex]\frac{2}{3} \pi r^3[/latex] cubic units.
Curved surface area = 2[latex]\pi r^2[/latex] sq. units.
Total surface area = 3[latex]\pi r^2 [/latex] sq. units.
14. Prism:
Volume of right prism = (Area of the base * height)cu. units
Lateral surface area of a right prism = (perimeter of the base * height)sq. units
Total surface area of a right prism = lateral area + 2(area of one base)sq. units
15. Circle:
Area = [latex]\pi r^2[/latex]
where, r = radius
Circumference = [latex]2 \pi r [/latex]
16. Semi-circle:
Area = [latex]\frac{1}{2} \pi r^2[/latex]
Circumference = [latex]\pi r + 2r[/latex]
17. Sector:
Area = [latex]\frac{\theta}{360} * \pi r^2[/latex]
Circumference = l + 2r[l = [latex]\frac{\theta}{360} * 2\pi r[/latex]]
where l = length of arc.
 Samples
Samples
1. A wheel makes 1000 revolutions in covering a distance of 88 km. Find the radius of the wheel?
Solution:
- Given that,
Number of revolutions made by wheel = 1000
Distance = 88 km
So, distance covered in 1 revolution = [latex]\frac{88 * 1000}{1000}[/latex] m = 88 m
Therefore, [latex]2 \pi r [/latex] = 88
⇒ 2 x [latex]\frac{22}{7}[/latex] x r = 88
⇒ r = 88 x [latex]\frac{7}{44}[/latex]
⇒ r = 14 m
Therefore, radius of the wheel = 14m.
- Given that,
Expenditure per hectare = Rs. 680
Area = [latex]\frac{680}{170}[/latex] = 4 hectares = 4 x 10000 sq.m.
So, Sides of the field = [latex]\sqrt{40000}[/latex] = 200 m.
Perimeter of the field = 4 x side = 4 x 200 = 800 m.
Therefore, Cost of putting the fence around it is
= 800 x 3 = Rs. 2400.
- Given that,
Time = 9 seconds
Rate = 6 km
Now, Distance covered in [latex]\frac{6 * 1000}{3600} * 9[/latex] = 15 m
Diagonal of the square field = 15 m.
Hence, Area of the square field = [latex]\frac{(15)^2}{2}[/latex] = [latex]\frac{225}{2}[/latex] = 112.5 sq.m.
- Given that,
Length = 22 cm
Breadth = 12 cm
Height = 7.5 cm
Now,
Diagonal of the cuboid = [latex]\sqrt{l^2 + b^2 + h^2}[/latex] = [latex]\sqrt{(22)^2 + (12)^2 + (7.5)^2}[/latex] = [latex]\sqrt{684.25}[/latex] = 26.15 cm.
Therefore, Diagonal of the cuboid = 26.15 cm.
- GGiven that,
Ratio between the curved surface area and total surface area of a right circular cylinder is 1 : 2
Total surface area = 616[latex]{cm}^2[/latex]
Now, [latex]\frac{2 \pi r h}{2 \pi r (h + r)}[/latex] = [latex]\frac{1}{2}[/latex]
⇒ [latex]\frac{h}{h + r}[/latex] = [latex]\frac{1}{2}[/latex]
⇒ h = r
Hence, total surface area = [latex]2 \pi r (h + r)[/latex] = 4 [latex]\pi r^2[/latex] (since, h = r)
Therefore, 4 [latex]\pi r^2[/latex] = 616
⇒ [latex] r^2[/latex] = 616 x [latex]\frac{1}{4}[/latex] x [latex]\frac{7}{22}[/latex] = 49
⇒ [latex] r[/latex] = 7
Thus, h = 7 cm and r = 7 cm
Therefore, Volume = [latex]\pi r^2 h[/latex]
= [latex]\frac{22}{7}[/latex] x 7 x 7 x 7 = 1078 [latex]{cm}^3[/latex].