Directions(1 – 5): Study the following information carefully and answer the given questions:

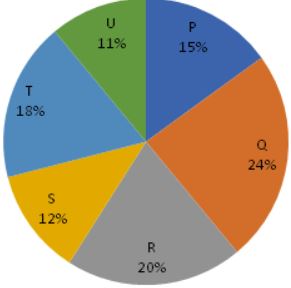
Following pie chart shows the total number of students in 6 different colleges.

Total Number of Students = 5000

1. Find the average number of students in college P, Q and S together?

A. 700 B. 650 C. 850 D. 900 E. None of these

2. Find the difference between the total number of students in college Q and R together to that of the college S and U together?

A. 1000 B. 1050 C. 1150 D. 1200 E. None of these

3. If 15 % and 20 % of students are going to symposium in college S and T respectively, then find the total number of students didn’t go to any symposium from both the colleges together?

A. 1230 B. 1570 C. 1340 D. 1450 E. None of these

4. The ratio of male and female students in College R and T is 3: 2 and 1: 2 respectively, then find the difference between the total number of male and female from both the colleges together?

A. 150 B. 200 C. 180 D. 100 E. 230

5. Total number of students in college Q is what percentage of total number of students in college R?

A. 100% B. 120% C. 110% D. 150% E. 140%

Answers and Explanations
1. Answer - Option C
Explanation -
The average number of students in college P, Q and S together
[latex]\Rightarrow (15 + 24 + 12) \times (\frac {5000}{100}) \times (\frac {1}{3})[/latex]
[latex]\Rightarrow[/latex] 850
2. Answer - Option B
Explanation -
The average number of students in college P, Q and S together
[latex]\Rightarrow (15 + 24 + 12) \times (\frac {5000}{100}) \times (\frac {1}{3})[/latex]
[latex]\Rightarrow[/latex] 850
The total number of students in college Q and R together
[latex]\Rightarrow (24 + 20) \times (\frac {5000}{100})[/latex]
The total number of students in college S and U together
[latex]\Rightarrow (12 + 11) \times (\frac {5000}{100})[/latex]
Required difference = [latex](\frac {5000}{100}) \times (44 – 23)[/latex]
[latex]\Rightarrow 50 \times 21 = 1050[/latex]
3. Answer - Option A
Explanation -
The total number of students didn’t go to any symposium from both the colleges together
[latex]\Rightarrow (\frac {12}{100}) \times 5000 \times (\frac {85}{100}) + (\frac {18}{100}) \times 5000 \times (\frac {80}{100})[/latex]
[latex]\Rightarrow 510 + 720 = 1230[/latex]
4. Answer - Option D
Explanation -
The ratio of male and female students in College R = 3 : 2
The ratio of male and female students in College T = 1 : 2
Total number of male in college R and T together
[latex]\Rightarrow (\frac {20}{100}) \times 5000 \times (\frac {3}{5}) + (\frac {18}{100}) \times 5000 \times (\frac {1}{3})[/latex]
[latex]\Rightarrow 600 + 300 = 900[/latex]
Total number of female in college R and T together
[latex]\Rightarrow (\frac {20}{100}) \times 5000 \times (\frac {2}{5}) + (\frac {18}{100}) \times 5000 \times (\frac {2}{3})[/latex]
[latex]\Rightarrow 400 + 600 = 1000[/latex]
Required difference = 1000 – 900 = 100
5. Answer - Option B
Explanation -
Required % = [latex](\frac {24}{20}) \times 100 = 120 [/latex] %

Directions(1 – 3): What value should come in the place of question mark (?) in the following questions?
1. [latex]\sqrt{6084}[/latex] ÷ 3 + 45 = ? – 12376 ÷ 7

A. 1839 B. 1945 C. 1757 D. 1653 E. None of these

2. [latex](\frac {5}{11}) of 5038 + 56 % of 1250 = {(?)}^{2} – 35[/latex]

A. 45 B. 30 C. 75 D. 55 E. None of these

3. [latex]{6}^{?} \times \sqrt{484} = 48090 ÷ 7 + 21642[/latex]

A. 7 B. 4 C. 9 D. 5 E. None of these

4. In a running race competition involving some boys and girls of an apartment, every member had to play exactly one race with every other member. It was found that in 10 races both the players were boys and in 45 races both the members were girls. Find the number of races in which one member was a boy and other was a girl.

A. 50 B. 40 C. 30 D. 20 E. None of these

5. A box consists of 15 balls numbered from 0 to 14. A boy picked a ball from the box and kept it in the bag after noting its number. He repeated this process 2 more times. What is the probability that the ball picked first by the boy is numbered higher than the ball picked second and the ball picked second by the boy is numbered higher than the ball picked third?

A. [latex]\frac{51}{3375}[/latex] B. [latex]\frac{67}{3375}[/latex] C. [latex]\frac{2197}{3375}[/latex] D. [latex]\frac{329}{3375}[/latex] E. None of these

Answers and Explanations
1. Answer - Option A
Explanation -
[latex](\frac {78}{3}) + 45 = x – (\frac {12376}{7})[/latex]
26 + 45 = x – 1768
X = 26 + 45 + 1768
X = 1839
2. Answer - Option D
Explanation -
[latex] (\frac{5}{11}) \times 5038 + (\frac {56}{100}) \times 1250 = {(x)}^{2} – 35[/latex]
[latex]2290 + 700 + 35 = {(x)}^{2}[/latex]
[latex]3025 = {(x)}^{2}[/latex]
X = 55
3. Answer - Option B
Explanation -
[latex]{6}^{?} \times 22 = (\frac {48090}{7}) + 21642[/latex]
[latex]{6}^{?} \times 22 = 6870 + 21642[/latex]
[latex]{6}^{?} = \frac {28512}{22}[/latex]
[latex]{6}^{?} = 1296[/latex]
[latex]{6}^{?} = {6}^{4}[/latex]
X = 4
4. Answer - Option A
Explanation -
Let the number of boys be x and girls be y.
No. of races played between boys = [latex]^{x}{C}_{2}[/latex] = 10 = x(x – 1) = 20 [latex]\Rightarrow[/latex] x = 5
Total number of boys participating in running race is 5.
No. of races played between girls = [latex]^{y}{C}_{2}[/latex] = 45 = y(y – 1) = 90 [latex]\Rightarrow[/latex] y = 10
Total number of girls participating in running race is 10.
Therefore, no of running races in which one player is boy and one is girl is,
= [latex] ^{5}{C}_{1} × ^{10}{C}_{1} = 5 \times 10 = 50[/latex]
5. Answer - Option C
Explanation -
Let the number on the ball picked first = a, second = b, third = c.
The order of a, b and c can be (a > b > c)
Number of ways selecting the first number = 13 (Because we can’t select 0 and 1)
Number of ways selecting the second number = 13 (Because we can’t select 0)
Number of ways selecting the third number = 13 (Because we can’t select first and third number)
Required probability = [latex]\frac {(13 \times 13 \times 13)}{153}[/latex]
= [latex]\frac {2197}{3375}[/latex]

1. Pipes A, B and C are fitted to a tank. Each pipe can act as either an inlet or outlet pipe. Pipes A, B and C take 4, 6 and 8 hours to fill the empty tank or empty the full tank. In the first hour, pipes A and C act as inlet and B act as outlet. In the second hour, pipes A and B act as inlet and pipe C act as outlet. In the third hour, pipes B and C act as inlet and pipe A act as outlet and the process goes on. When will the tank be filled?

A. In the 5th hour B. In the 10th hour C. In the 12th hour D. In the 15th hour E. None of these

2. Meena’s capital is 2/3 times more than Mira’s capital. Mira invested her capital at 40% per annum for 2 years (compounded annually). At what rate % per annum simple interest should Meena invest her capital so that after 2 years, they both have the same amount of capital?

A. 10% B. 15.2% C. 8.8% D. 20% E. None of these

3. Look at this series: 544, 509, 474, 439, ... What number should come next?

A. 414 B. 404 C. 445 D. 420 E. 444

4. Find the missing number in the given series 12, 38, 116, 350, 1052, ?

A. 2200 B. 1800 C. 3158 D. 2800 E. 2000

5. Find the missing number in the given series 5,28,57,88,125

A. 147 B. 156 C. 186 D. 166 E. 200

Answers and Explanations
1. Answer - Option A
Explanation -
In a cycle of 3 hours, Pipes A, B and C are acting as inlet pipes for 2 hours each and they are acting as outlet pipes for an hour each.
LCM of 4, 6 and 8 = 24
Total = 24 units
A = 6 units per hour
B = 4 units per hour
C = 3 units per hour
Hence, Part of a tank filled in 3 hours (1 cycle) = 2 * (6 + 4 + 3) – (6 + 4 + 3)
= (6 + 4 + 3) = 13
Remaining = 24 – 13 = 11 units
4th hour = 11 – (6 + 3 – 4) = 11 – 5 = 6 units
5th hour pipes can fill 7 units
Thus, tank will be filled in 5th hour.
2. Answer - Option C
Explanation -
Let the capital of Mira = 3. Then Capital of Meena = [latex]\frac {2}{3}[/latex] times more than Mira
Capital of Meena = [latex]\frac {2}{3} \times 3 + 3 = 5[/latex]
From the given data, we get the below equation.
[latex]\Rightarrow Mira’s capital {(1 + r )}^{n}[/latex] = Meena’s capital + [latex][Meena’s capital \times n \times \frac {R}{100}][/latex]
[latex]\Rightarrow 3{(1 + \frac {40}{100})}^{2} = 5 + [5 \times 2 \times \frac {R}{100}][/latex]
[latex]\Rightarrow 3 \times \frac {140}{100} \times \frac {140}{100} = 5 + \frac {10R}{100}[/latex]
[latex]\Rightarrow[/latex] R = 8.8%
3. Answer - Option B
Explanation -
This is a simple subtraction series. Each number is 35 less than the previous number.
4. Answer - Option C
Explanation -
38 × 3 + 2 = 116
116 × 3 + 2 = 350
350 × 3 + 2 = 1052
1052 × 3 + 2 = 3158
5. Answer - Option D
Explanation -
57 = 29 + 28
88 = 31 + 57
125 = 37 + 88
166 = 41 + 125