Q1. A and B together can complete a job in 16 days. Both B and C, working alone can finish the same job in 12 days, A and B commence work on the job, and work for 4 days, whereupon A leaves, B continues for 2 more days, and then he leaves too, C now starts working and finishes the job. How many days will C require?

A. 5 days B. 8 days C. 3 days D. 7 days

Answer: D
Explanation: (A + B)' 4 days work = [latex]\frac {4}{16} = \frac {1}{4}[/latex]
B's 2 days work = [latex]\frac {2}{12} = \frac {1}{6}[/latex]
therefore, Remaining work = 1 - [latex](\frac {1}{4} + \frac {1}{6})[/latex]
[latex] \frac {7}{12} [/latex]
therefore, [latex]\frac {\frac {7}{12}}{\frac {1}{12}}[/latex] = 7 days
Q2. A laborer was appointed by a contractor on the condition he would be paid Rs 150 for each day of his work but would be, fined a the rate of Rs 30 per day for his absence. After 20 days, the contractor paid the laborer’s 2820. Find the number of days he worked:

A. 13 days B. 19 days C. 5 days D. 12 days

Answer: B
Explanation: Let the required number of days = [latex] x [/latex] days
So, [latex] 150x - (20 - x) 30 [/latex] = 2820
[latex] x = 19[/latex] days
Q3. A can do a piece of work in 120 days and B can do it in 150 days. They work together for 20 days. Then A leaves and B continues the work. 12 days after that, C joins the work and the work is completed in 48 more days. In how many days C can do it alone?

A. 225 B. 220 C. 230 D. None of these

Answer: D
Explanation: A and B per day work = [latex]\frac {1}{120} + \frac {1}{150} = \frac {27}{1800}[/latex]
A and B work in 20 days = [latex]\frac {20 \times 27}{1800}[/latex]
B work in 12 days = [latex]\frac {12}{150} = \frac {144}{1800}[/latex]
Remaining work = 1 - [latex](\frac {540}{1800} + \frac {144}{1800})[/latex]
= [latex] \frac {1116}{1800} [/latex]
B and C, 1 day work = [latex] \frac {1116}{\frac {1800}{48}} [/latex]
C per day work = [latex] \frac {1116}{1800 \times 48} - \frac {1}{150}[/latex]
[latex]\frac {540}{1800 \times 48} = \frac {1}{160}[/latex]
So no. of days by C to complete the work = 160
Q4. A builder decided to build a farmhouse in 40 days. He employed 100 men in beginning and 100 more after 35 days and completed the work on time. If no additional men would have been employed, then find the delay.

A. 5 days B. 6 days C. 8 days D. 10 days

Answer: A
Explanation: After 35 days 200 men complete the remaining work in 5 days
100 men can complete this work in [latex]\frac {200}{100} \times 5[/latex]
= 10 days
Delay = (35 + 10) - 40 = 5 days
Q5. Ramesh can finish a job in 20 days. He worked for 10 days alone and completed the remaining job working with Dinesh, in 2 days. How many days would both Dinesh and Ramesh together take to complete the entire job?

A. 4 B. 5 C. 10 D. 12

Answer: A
Explanation: Ramesh alone finished [latex] \frac {1}{2} [/latex] of the work in 10 days.
Remaining [latex] {1}{2} [/latex] was finished by Ramesh and Dinesh together in 2 days.
Therefore, they both together can finish the complete job in 4 days.

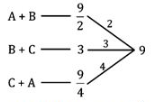
Q1. A and B working together can do a piece of work in 4 1/2 hours. B and C working together can do it in 3 hours. C and A working together can do it in 2 1/4 hours. All of them begin work at the same time. Find how much time they will take to finish the piece of work?

A. 3 hours B. 2 hours C. 2.5 hours D. 1 hours

Answer: B
Explanation: Total efficiency = [latex]\frac {9}{2} [/latex]
Time = 2 hours
Q2. Ram decided to plow farmland in 50 days. He employed 50 men in the beginning and 50 more after 35 days and completed the construction in stipulated time. If he had not employed the additional men, how many days behind schedule would it have been finished?

A. 5 days B. 6 days C. 8 days D. 10 days

Answer: A
Explanation: Given that, 50 men employed for 35 days and 50 more men employed for 15 days so that the work could be finished in 50 days.
Thus, the total work = [latex] 50 \times 35 + (50 + 50) 15 [/latex] = 3250
Suppose, it takes [latex] x [/latex] days to finish the whole work if additional men were not employed.
So, we have an equation here.
[latex] 50 \times x [/latex] = 3250
[latex] x [/latex] = 65 days
Therefore, it takes 15 days more than the stipulated time.
Q3. The work done by a woman in 8 hours is equal to the work done by a man in 6 hours and by a boy in 12 hours. If working 6 hours per day 9 men can complete a work in 6 days then in how many days can 12 men, 12 women and 12 boys together finish the same work working 8 hours per day?

A. 1 [latex] \frac {1}{2} [/latex] days B. 3 [latex] \frac {2}{3} [/latex] days C. 3 days D. 2 [latex] \frac {1}{2} [/latex] days

Answer: A
Explanation: 8 Women = 6 Men = 12 Boys
12M + 12W + 12B = 12M + 9M + 6M = 27M
Now, applying the above formula, we have
[latex]9 \times 6 \times 6 = 27 \times 8 \times [D]_[2] [/latex]
[latex] [D]_[2] = \frac {9 \times 6 \times 6}{27 \times 8} = 1 \frac {1}{2} [/latex] days
Q4. A and B can do a piece of work in 10 days, B and C in 15 days and C and A in 20 days. They all work at it for 6 days, and then A leaves, and B and C go on together for 4 days more. If B then leaves, how long will C take to complete the work?

A. 20 days B. 25 days C. 10 days D. 15 days

Answer: C
Explanation: Amount of work done by A, B and C together in aday is [latex] \frac {6 + 4 + 3}{2 \times 60} = \frac {13}{120} [/latex]
Work done by all in 6 days = [/latex] \frac {13}{120} [/latex]
Work done by B and C in 4 days = [latex]\frac {4}{15}[/latex]
Remaining work = 1 - [latex](\frac {13}{20} + \frac {4}{15})[/latex]
= [latex]\frac {1}{2}[/latex], which is to be done C
Now, from the question,
C alone can do the whole work in [latex]\frac {\frac {120}{18}\times {10}}{10 - \frac {120}{18}}[/latex] = 120 days
therefore, [latex]\frac {1}{12}[/latex] of the work is done by C [latex]\frac {120}{12}[/latex] = 10 days
Q5. Amit and Sujit together can complete an assignment of Data entry in 5 days. Sujit’s speed is 80 % of Amit’s speed and the total key depressions in the assignment are 5,76,000. What is Amit’s speed in key depressions per hour if they work for 4 hours a day?

A. 14800 B. 16400 C. 16000 D. 17200

Answer: C
Explanation: Amit + Sujith = 5 days
Let Amit = [latex] x [/latex] days
Sujith = [latex]\frac {180 x}{100} = \frac {4 x}{5}[/latex] days
now,
[latex]\frac {1}{x} + \frac {5}{4x} = \frac {1}{5}[/latex]
[latex]\frac {4 + 5}{4 x} = \frac {1}{5} [/latex]
[latex] \frac {45}{4} [/latex]
therefore, Amit = [latex] \frac {45}{4} [/latex], Sujit = [latex] \frac {45}{4} \times \frac {4}{5}[/latex] = 9
therefore, Ratio of their work = 5 : 4
therefore, Required key depressions per hour a day = [latex]\frac {5}{9} \times 576000 \times \frac {1}{4} \times \frac {1}{5}[/latex] = 16000

Q1. A is twice efficient as B. A and B together do the same work in as much time as C and D can do together. If the ratio of the number of alone working days of C to D is 2:3 and if B worked 16 days more than C then no of days which A worked alone?

A. 18 Days B. 20 Days C. 30 Days D. 36 Days

Answer: A
Explanation: Assume working days
[latex] A = x, B = 2x, C = 2y, D = 3y [/latex]
[latex] \frac {1}{x} + \frac {1}{2x} = \frac {1}{2y} + \frac {1}{3y} [/latex]
And [latex] 2x - 2y [/latex] = 16
Solving we get [latex] x [/latex] = 18 days.
Q2. A can do a piece of work in 40 days B can do the same piece of work in 60 days. A and B started the work together in the first 15 days A worked with 50% of his efficiency, in the next 15days B worked with 50% of his efficiency. Now in how many days does the remaining work will be completed if both of them work with their full efficiencies?

A. 1 Day B. 1.5 Day C. 2 Days D. 2.5 Days

Answer: B
Explanation: [latex] 15 \times (\frac {1}{80} + {1}{60}) + 15 \times (\frac {1}{120} + {1}{40}) + x \times (\frac {1}{40} + \frac {1}{60}) [/latex] = 1
[latex] X= \frac {3}{2} = 1.5 [/latex]
Q3. A can do a piece of work in 30 days, B can do in 45 days and C can do the same work alone in 60 days. If on the first day A worked alone and on the second day A and B worked together and on the third day A and C worked together. If they repeat the cycle as follows then in how many days total work can be completed?

A. 21 Days B. 21 [latex] \frac {7}{8} [/latex] Days C. 21 [latex] \frac {5}{6} [/latex] Days D. 21 [latex] \frac {4}{9} [/latex] Days

Answer: C
Explanation: First day = [latex] \frac {1}{30} [/latex]
Second day = [latex] \frac {1}{30} + \frac {1}{45} [/latex]
Third day = [latex] \frac {1}{30} + \frac {1}{60} [/latex]
3 days work = [latex] \frac {3}{30} + {1}{45} + {1}{60} [/latex] = [latex] \frac {25}{180} [/latex]
[latex] 3 \times 7 [/latex] = 21 days work = [latex] \frac {175}{180} [/latex]
Now [latex] \frac {1}{36} [/latex] work is left which can be completed by A alone
[latex] \frac {1}{36} \times 30 = \frac {5}{6} [/latex]
[latex] 21 + \frac {5}{6} = 21 \frac {5}{6} [/latex] Days
Q4. Ramu completes 30% of work in 7.5 days. Raju is 50% as efficient as Ramu, Venu is 50% as efficient as Raju. Now Raju and Venu joined with Ramu for the rest of the work than in how many days will take to complete the work?

A. 9 Days B. 10 Days C. 12 Days D. 15 Days

Answer: B
Explanation: Ramu takes 25 days to complete work.
Raju = 50 days Venu = 100 days
Now 70 % of work is left
They can complete whole work in = [latex] \frac {1}{\frac {1}{25}} + \frac {1}{50} + {1}{100} [/latex]
[latex] \frac {100}{7} [/latex] days then 70% in 10 days
Q5. A can do a piece of work in 21days. B is 50% more efficient than A. C is twice efficient than B. A started the work alone and worked for some days and left the work then B and C joined together and completed the work in 2 days. Then how many days does A worked alone?

A. 7 Days B. 12 Days C. 14 Days D. 21 Days

Answer: B
Explanation: A = 21 B = 14 C =7
[latex] \frac {x}{21} + 2 \times (\frac {1}{14} + \frac {1}{7}) [/latex] = 1
[latex] x [/latex] = 12.