 Introduction
Introduction
Mensuration is a topic in Geometry which is a branch of mathematics. Mensuration deals with length, area, and volume of different kinds of shape- both 2D and 3D. The article IBPS RRB Mensuration Quiz 1 provides information about Mensuration, an important topic of Mathematics Consists of different types of Mensuration questions with solutions useful for candidates preparing for different competitive examinations perticularly IBPS, SBI PO, SBI Clerks, SSC MTS, SSC CGL, SSC CHSL, RRB, RRB ALP/Technical Exams/Junior Engineer Recruitment Exams, CAT and etc.
 Quiz
Quiz
1. A right triangular pyramid XYZB is cut from cube as shown in figure. The side of cube is 16 cm. X, Y and Z are mid points of the edges of the cube. What is the total surface area (in [latex]{cm}^{2}[/latex]) of the pyramid?
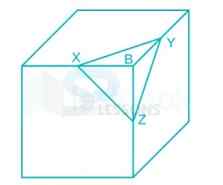
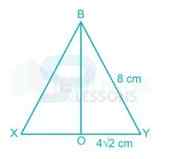 In the figure;
[latex]{(XY)}^{2}[/latex] = 64 + 64
XY = 8√2 cm
∴ YZ = ZX = 8√2 cm
∴ Base area of the pyramid = [latex]\frac{√3}{4}[/latex] × 128 = 32√3 [latex]{cm}^{2}[/latex]
Height of rest three surfaces of the pyramid (as in above figure) = 4√2 cm
Area of 3 surfaces of pyramid = 3 × [latex]\frac{1}{2}[/latex] × 4√2 × 8√2 = 96 [latex]{cm}^{2}[/latex]
Total surface area = 96 + 32√3 = 32 (3 + √3) [latex]{cm}^{2}[/latex]
2. In the given figure, two squares of sides 8 cm and 20 cm are given. What is the area (in cm2) of the shaded part?
In the figure;
[latex]{(XY)}^{2}[/latex] = 64 + 64
XY = 8√2 cm
∴ YZ = ZX = 8√2 cm
∴ Base area of the pyramid = [latex]\frac{√3}{4}[/latex] × 128 = 32√3 [latex]{cm}^{2}[/latex]
Height of rest three surfaces of the pyramid (as in above figure) = 4√2 cm
Area of 3 surfaces of pyramid = 3 × [latex]\frac{1}{2}[/latex] × 4√2 × 8√2 = 96 [latex]{cm}^{2}[/latex]
Total surface area = 96 + 32√3 = 32 (3 + √3) [latex]{cm}^{2}[/latex]
2. In the given figure, two squares of sides 8 cm and 20 cm are given. What is the area (in cm2) of the shaded part?
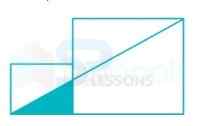
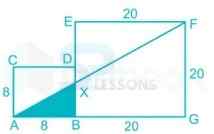 Here ∆AXB and ∆AFG will be similar
⇒[latex]\frac{8}{28}[/latex] =[latex]\frac{BX}{20}[/latex]
⇒ BX =[latex]\frac{40}{7}[/latex]
⇒ Area of ∆AXB = [latex]\frac{1}{2}[/latex] × (AB × BX)
⇒ Area of ∆AXB = ½ × (8 × [latex]\frac{40}{7}[/latex])
∴ Area of ∆AXB = [latex]\frac{160}{7}[/latex] [latex]{cm}^{2}[/latex]
3. A hemisphere is kept on top of a cube. Its front view is shown in the given figure. The total height of the figure is 21 cm. The ratio of curved surface area of the hemisphere and total surface area of cube is 11 ∶ 42. What is the total volume (in cm 3) of figure?
Here ∆AXB and ∆AFG will be similar
⇒[latex]\frac{8}{28}[/latex] =[latex]\frac{BX}{20}[/latex]
⇒ BX =[latex]\frac{40}{7}[/latex]
⇒ Area of ∆AXB = [latex]\frac{1}{2}[/latex] × (AB × BX)
⇒ Area of ∆AXB = ½ × (8 × [latex]\frac{40}{7}[/latex])
∴ Area of ∆AXB = [latex]\frac{160}{7}[/latex] [latex]{cm}^{2}[/latex]
3. A hemisphere is kept on top of a cube. Its front view is shown in the given figure. The total height of the figure is 21 cm. The ratio of curved surface area of the hemisphere and total surface area of cube is 11 ∶ 42. What is the total volume (in cm 3) of figure?
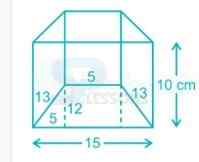 As we know, volume of the trapezium prism = base area(area of trapezium) × height
⇒ 1200 = [latex]\frac{1}{2}[/latex] × (5 + 15) × 12 × h
⇒ h = 10 cm
∵ Lateral surface area = perimeter of trapezium × height
Total surface area of the trapezoidal prism
⇒ 2 × base area(area of trapezium) + lateral surface area
⇒ 2 × [latex]\frac{1}{2}[/latex] × (5 + 15) × 12 + perimeter of trapezium × height
⇒ 240 + (15 + 13 + 5 + 13) × 10
⇒ 240 + 460 = 700 [latex]{cm}^{2}[/latex]
∴ Total surface area of the trapezoidal prism = 700 [latex]{cm}^{2}[/latex]
As we know, volume of the trapezium prism = base area(area of trapezium) × height
⇒ 1200 = [latex]\frac{1}{2}[/latex] × (5 + 15) × 12 × h
⇒ h = 10 cm
∵ Lateral surface area = perimeter of trapezium × height
Total surface area of the trapezoidal prism
⇒ 2 × base area(area of trapezium) + lateral surface area
⇒ 2 × [latex]\frac{1}{2}[/latex] × (5 + 15) × 12 + perimeter of trapezium × height
⇒ 240 + (15 + 13 + 5 + 13) × 10
⇒ 240 + 460 = 700 [latex]{cm}^{2}[/latex]
∴ Total surface area of the trapezoidal prism = 700 [latex]{cm}^{2}[/latex]

- A. 48[√3 + 1]
B. 24[4 + √3]
C. 28[6 + √3]
D. 28[6 + √3]
 In the figure;
[latex]{(XY)}^{2}[/latex] = 64 + 64
XY = 8√2 cm
∴ YZ = ZX = 8√2 cm
∴ Base area of the pyramid = [latex]\frac{√3}{4}[/latex] × 128 = 32√3 [latex]{cm}^{2}[/latex]
Height of rest three surfaces of the pyramid (as in above figure) = 4√2 cm
Area of 3 surfaces of pyramid = 3 × [latex]\frac{1}{2}[/latex] × 4√2 × 8√2 = 96 [latex]{cm}^{2}[/latex]
Total surface area = 96 + 32√3 = 32 (3 + √3) [latex]{cm}^{2}[/latex]
2. In the given figure, two squares of sides 8 cm and 20 cm are given. What is the area (in cm2) of the shaded part?
In the figure;
[latex]{(XY)}^{2}[/latex] = 64 + 64
XY = 8√2 cm
∴ YZ = ZX = 8√2 cm
∴ Base area of the pyramid = [latex]\frac{√3}{4}[/latex] × 128 = 32√3 [latex]{cm}^{2}[/latex]
Height of rest three surfaces of the pyramid (as in above figure) = 4√2 cm
Area of 3 surfaces of pyramid = 3 × [latex]\frac{1}{2}[/latex] × 4√2 × 8√2 = 96 [latex]{cm}^{2}[/latex]
Total surface area = 96 + 32√3 = 32 (3 + √3) [latex]{cm}^{2}[/latex]
2. In the given figure, two squares of sides 8 cm and 20 cm are given. What is the area (in cm2) of the shaded part?

- A. [latex]\frac{120}{7}[/latex]
B. [latex]\frac{160}{7}[/latex]
C. [latex]\frac{180}{7}[/latex]
D. [latex]\frac{240}{13}[/latex]
 Here ∆AXB and ∆AFG will be similar
⇒[latex]\frac{8}{28}[/latex] =[latex]\frac{BX}{20}[/latex]
⇒ BX =[latex]\frac{40}{7}[/latex]
⇒ Area of ∆AXB = [latex]\frac{1}{2}[/latex] × (AB × BX)
⇒ Area of ∆AXB = ½ × (8 × [latex]\frac{40}{7}[/latex])
∴ Area of ∆AXB = [latex]\frac{160}{7}[/latex] [latex]{cm}^{2}[/latex]
3. A hemisphere is kept on top of a cube. Its front view is shown in the given figure. The total height of the figure is 21 cm. The ratio of curved surface area of the hemisphere and total surface area of cube is 11 ∶ 42. What is the total volume (in cm 3) of figure?
Here ∆AXB and ∆AFG will be similar
⇒[latex]\frac{8}{28}[/latex] =[latex]\frac{BX}{20}[/latex]
⇒ BX =[latex]\frac{40}{7}[/latex]
⇒ Area of ∆AXB = [latex]\frac{1}{2}[/latex] × (AB × BX)
⇒ Area of ∆AXB = ½ × (8 × [latex]\frac{40}{7}[/latex])
∴ Area of ∆AXB = [latex]\frac{160}{7}[/latex] [latex]{cm}^{2}[/latex]
3. A hemisphere is kept on top of a cube. Its front view is shown in the given figure. The total height of the figure is 21 cm. The ratio of curved surface area of the hemisphere and total surface area of cube is 11 ∶ 42. What is the total volume (in cm 3) of figure?
- A. 3318.33
B. 3462.67
C. 3154.67
D. 3154.67
- A. 100 sq cm
B. 25 sq cm
C. 50 sq cm
D. 160 sq cm
- A. 400 [latex]{cm}^{2}[/latex]
B. 500 [latex]{cm}^{2}[/latex]
C. 700 [latex]{cm}^{2}[/latex]
D. 600 [latex]{cm}^{2}[/latex]
 As we know, volume of the trapezium prism = base area(area of trapezium) × height
⇒ 1200 = [latex]\frac{1}{2}[/latex] × (5 + 15) × 12 × h
⇒ h = 10 cm
∵ Lateral surface area = perimeter of trapezium × height
Total surface area of the trapezoidal prism
⇒ 2 × base area(area of trapezium) + lateral surface area
⇒ 2 × [latex]\frac{1}{2}[/latex] × (5 + 15) × 12 + perimeter of trapezium × height
⇒ 240 + (15 + 13 + 5 + 13) × 10
⇒ 240 + 460 = 700 [latex]{cm}^{2}[/latex]
∴ Total surface area of the trapezoidal prism = 700 [latex]{cm}^{2}[/latex]
As we know, volume of the trapezium prism = base area(area of trapezium) × height
⇒ 1200 = [latex]\frac{1}{2}[/latex] × (5 + 15) × 12 × h
⇒ h = 10 cm
∵ Lateral surface area = perimeter of trapezium × height
Total surface area of the trapezoidal prism
⇒ 2 × base area(area of trapezium) + lateral surface area
⇒ 2 × [latex]\frac{1}{2}[/latex] × (5 + 15) × 12 + perimeter of trapezium × height
⇒ 240 + (15 + 13 + 5 + 13) × 10
⇒ 240 + 460 = 700 [latex]{cm}^{2}[/latex]
∴ Total surface area of the trapezoidal prism = 700 [latex]{cm}^{2}[/latex]
1. Two right circular cylinders of equal volume have their heights in the ratio 1 : 2. The ratio of
their radii is?
- A. √2:1
B. 2 : 1
C. 1 : 2
D. 1 : 4
- A. 3.696 kg
B. 3.6 kg
C. 36 kg
D. 36.9 kg
- A. 1 cm
B. 2 cm
C. 3 cm
D. 6 cm
- A.[latex]\frac{4}{3}[/latex]
B. [latex]\frac{2}{3}[/latex]
C. [latex]\frac{3}{4}[/latex]
D.[latex]\frac{3}{2}[/latex]
- A. 1663.2
B. 1500
C. 1747.6
D. 2000
1. The lateral surface area of a cylinder is 1056 cm² and its height is 16 cm. Find its volume?
- A. 4545 cm³
B. 4455 cm³
C. 5445 cm³
D. 5544 cm³
- A. 942.86
B. 314.29
C. 628.57
D.450.76
- A.1232 cm³
B. 1848 cm³
C. 1632 cm³
D. 1078 cm³
- A. 8
B. 12
C. 24
D. [latex]{\sqrt[3]{2}}[/latex]
- A. 3 : 1
B. 27 : 1
C. 1:3
D. 1:27





