1. In how many different ways can the letters of the word "CANDIDATE" be arranged in such a way that the vowels always come together?

A. 4320 B. 1440 C. 720 D. 840

2. In how many different ways can the letters of the word "RADIUS" be arranged in such a way that the vowels occupy only the odd positions?

A. 72 B. 144 C. 532 D. 36

3. If 5:7 is the ratio of the present ages of Shahul and Ravi respectively. The difference between their ages is 6 years then what is the age of Shahul?

A. 15 years B. 24 years C. 17 years D. 19 years

4. The ratio of present ages of Mani and Dilip is 4:3, after 3 years Mani's age will be 39 years then the present age of Dilip is :

A. 20 years B. 27 years C. 23 years D. 25 years

5. The ratio of the age of Hari to that of Charan is 6:7. If Hari is 4 years younger than Charan then what will be the ratio of the ages of Hari and Charan after 4 years?

A. 7 : 8 B. 1 : 4 C. 2 : 5 D. 5 : 6

Answers and Explanations
1. Answer - Option A
Explanation -
There are 9 letters in the given word, out of which 4 are vowels.
In the word "CANDIDATE" we treat the vowels "AIAE" as one letter.
Thus, we have CNDDT(AIAE).
Now, we have to arrange 6 letters, out of which D occurs twice.
Therefore, number of ways of arranging these letters = [latex]\frac {6!}{2!} = \frac {720}{2} = 360[/latex] ways.
Now, AIAE has 4 letters, in which A occurs 2 times and the rest are different.
Number of ways of arranging these letters = [latex]\frac {4!}{2!} = \frac {1 x 2 x 3 x 4}{2} = 12[/latex]
Therefore, required number of words = (360 x 12) = 4320.
2. Answer - Option D
Explanation -
There are 6 different letters in the given word, out of which there are 3 vowels and 3 consonants.
Let us mark these positions as under:
[1] [2] [3] [4] [5] [6]
Now, 3 vowels can be placed at any of the three places out of 3 marked 1, 3 and 5.
Number of ways of arranging the vowels = [latex]^{3}{P}_{3} = 3! = 6[/latex] = 3! = 6 ways.
Also, the 3 consonants can be arranged at the remaining 3 positions.
Number of ways of these arrangements = [latex]^{3}{P}_{3} = 3! = 6[/latex] ways.
Therefore, total number of ways = 6 x 6 = 36.
3. Answer - Option A
Explanation -
Let the present age of Shahul and Ravi be 5X and 7X respectively.
Given that 7X - 5X = 6
2X = 6 [latex]\Rightarrow[/latex] X = 3
Then Shahul's present age is 5X = 5(3) = 15.
Hence, the answer is 15 years.
4. Answer - Option B
Explanation -
Let the present ages of Mani and Dilip is 4X and 3X respectively.
After 3 years Mani's age is 4X + 3
4X + 3 = 39
4X = 36
X = 9.
Then the present age of Dilip is 3X = 3(9) = 27
Hence the answer is 27 years.
5. Answer - Option A
Explanation -
Ratio of the ages of Hari and Charan is 6:7.
Let the ages of Hari and Charan be 6X years and 7X years respectively.
Then 7X - 6X = 4 (since Hari is 4 years younger)
X = 4.
Now, the required ratio is 6X + 4 : 7X + 4
6(4) + 4 : 7(4) + 4 = 28 : 32
7 : 8
Hence the answer is 7 : 8

1. Sum of six consecutive numbers that are divisible by 3 is 99. Find the sum of the first two numbers.

A. 30 B. 21 C. 14 D. 15

2. 10% of ?% of 1000 = 150

A. 150 B. 1500 C. 300 D. 3000

3. The average of four consecutive odd integers is 24 less than the sum of these integers. Then which will be the largest of them?

A. 27 B. 22 C. 24 D. 20

4. The arithmetic mean of the five consecutive numbers a, a + 1, a+ 2, a + 3 and a + 4 is A, then the value of the median of these numbers is equal to:

A. 2 B. a + 3 C. a D. a + 4

5. A man lent out Rs.9600 at [latex]\frac {9}{2}[/latex] % per annum for a year and 9 months. At the end of the duration, the amount he earned as S.I was:

A. 567 B. 756 C. 874 D. 784

Answers and Explanations
1. Answer - Option B
Explanation -
Difference between successive numbers divisible by 3 will be 3. Therefore, the series takes the form as below.
x - 6,x - 3, x, x + 3, x +6, x + 9
Sum of all terms in the series = 99 = x - 6 + x - 3 + x + x + 3 + x + 6 + x + 9 = 6x + 9
6x + 9 = 99
Or 6x = 90
Or x = 15
Sum of first two numbers = x - 6 + x - 3 = 2x - 9 = 2(15) - 9 = 21
2. Answer - Option A
Explanation -
Let the number to be found be N
Then, 10% of N% of 1000 = 150
Or [latex](\frac {10}{100})x(\frac {N}{100}) x 1000 = 150[/latex]
Or N = [latex]\frac {(150 x 100 x 100)}{(10 x 1000)} = 150[/latex]
3. Answer - Option A
Explanation -
Let the x, x + 2, x + 4 and x + 6 be the 4 consecutive odd integers.
We have to find the largest integer x + 6.
It is given that the average of these numbers is 24.
i,e., [latex]\frac {(x + x + 2 + x + 4 + x + 6)}{4} [/latex] = 24
4x + 12 = 24 x 4
4x = 84
x = [latex]\frac {84} {4} [/latex] = 21
Then x + 6 = 21 + 6 = 27
Hence, the answer is 27.
4. Answer - Option A
Explanation -
Let a, a + 1, a + 2, a + 3 and a + 4 be the given 5 consecutive numbers.
We have to find value of their median.
i.e, middle number of them = a + 2
It is given that, their average = arithmetic mean = A = [latex]\frac {(a + a + 1 + a + 2 + a + 3 + a + 4)}{5}[/latex]
A = [latex]\frac {(5a + 10)}{5} = \frac {5(a+2)}{5} = a + 2 [/latex]
a + 2 = A.
5. Answer - Option B
Explanation -
Given that, principal = P = Rs.9600, R = [latex]\frac {9}{2}[/latex] % and T = 1 year and 9 months = 1 + [latex]\frac {9}{12}[/latex] year = [latex]\frac {7}{4}[/latex] years.
Now, we have to find the S.I for [latex]\frac {7}{4}[/latex] years.
S.I = [latex]\frac {PRT}{100}[/latex] = Rs. [latex]9600 \times \frac {9}{2} \times \frac {7}{4} \times \frac {1}{100}[/latex] = 12 x 9 x 7 = 756
Hence, the required S.I amount is Rs.756

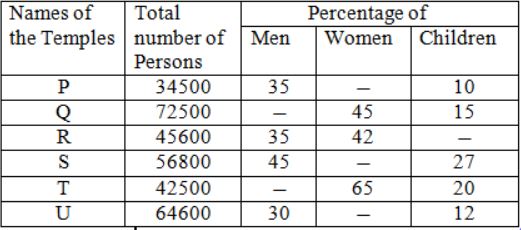
Direction[1-5]: Study the following table carefully and answer the questions given below:

The number of persons visiting six different temples and percentage of Men, Women and Children visiting those temples

1. The number of men visiting Temples S are approximately what percent of the total number of person visiting all the temples together?

A. 8% B. 12% C. 10.5% D. 15%

2. The number of children visiting Temple R is what per cent of the number of children visiting Temple T and U together?

A. 54.5% B. 44.5% C. 64.5% D. 67.5%

3. What is the total number of visitor children and men together visiting Temple Q and Temple R together?

A. 62523 B. 66358 C. 64323 D. 66323

4. What is the approximate average number of women visiting all the Temples together?

A. 25692 B. 25212 C. 25292 D. 22292

5. What is the ratio of the number of women visiting Temple P to that of those visiting Temple R?

A. 6325 : 6384 B. 6325 : 6383 C. 6325 : 6385 D. 6325 : 6388

Answers and Explanations
1. Answer - Option A
Explanation -
Total number of men visiting Temples S
= [latex]\frac {(56800 \times 45)}{100}[/latex] = 25560
Total number of person visiting all the temples
= (34500 + 72500 + 45600 + 56800 + 42500 + 64600) = 316500
Required percentage = [latex]\frac {(25560 \times 100)}{316500}[/latex] = 8%
2. Answer - Option C
Explanation -
Total number of children visiting Temple R
= [latex]\frac {(45600 \times 23)}{100} = 10488[/latex]
Total number of children visiting Temple T and U
= [latex]\frac {(42500 \times 20)}{100} + \frac {(64600 \times 12)}{100}[/latex]
= 8500 + 7752 = 16252
Required percentage = [latex]\frac {(10488 \times 100)}{16252} = 64.5 [/latex]%
3. Answer - Option D
Explanation -
Total number of visitors children and men together visiting Temple Q
= [latex]\frac {(72500 \times 55)}{100}[/latex] = 39875
Total number of visitors children and men together visiting Temple R
= [latex]\frac{(45600 \times 58)}{100}[/latex] = 26448
Required number = (39875 + 26448) = 66323
4. Answer - Option C
Explanation -
Total number of women visiting all the Temples
= [latex]\frac {(34500 \times 55)}{100} + \frac {(72500 \times 45)}{100} + \frac {(45600 \times 42)}{100} + \frac {(56800 \times 28)}{100} + \frac {(42500 \times 65)}{100} + \frac {(64600 \times 58)}{100}[/latex]
= (18975 + 32625 + 19152 + 15904 + 27625 + 37468) = 151749
Required average = [latex]\frac {151749}{6}[/latex] = 25291.5 = 25292
5. Answer - Option A
Explanation -
Total number of women visiting Temple P
= [latex]\frac {(34500 \times 55)}{100}[/latex] = 18975
Total number of women visiting Temple R
= [latex]\frac {(45600 \times 42)}{100} = 19152[/latex]
Required ratio = [latex]\frac {18975}{19152} = 6325 : 6384 [/latex]