1. Abhishek divided his total saving into three parts Rs (P+1000), Rs (P+1200), Rs (P-800) and invested at the rates of 12%,10% and 8% respectively. Simple interest gets from second part is rs 500 more than that of the third part at the end of the second year. Had he invested his total saving on C.I. at the rate of 10% per annum, find the interest earned by the man after two years?

A. 2300 B. 2500 C. 6473 D. 6381 E. 2373

2. Twenty men were employed to do same work in a certain time. But when one third of the scheduled time was over, it was found that only one – quarter of the total work was completed. How many more men should now be employed to complete the work in three – fourths of the originally scheduled time?

A. 20 B. 40 C. 48 D. 28 E. None of these

3. Amit goes to mall to buy a TV and a washing machine. He bargains for a 10% discount on the washing machine and 25% discount on TV. However, the shopkeeper, by mistake, interchanged the discount percentage figures while making the bill and Amit paid accordingly. When compared to what he should pay for his purchases, what percentage did Amit pay extra given that the washing machine costs 60% as much as the TV.

A. 4.65% B. 6.55% C. 3.26% D. 2.2% E.5.5%

4. P and R entered into partnership business with the capital of Rs.X and Rs. (x+12000), after one year Q joined them with capital of Rs.(x+8000) at the end of second year P and Q with draw their capital and R invest for one more year, if P, Q and R gets profit in the ratio of 8:6:21 respectively. Find sum of capital invested by all three?

A. Rs. 66000 B. Rs. 67000 C. Rs. 68000 D. Rs. 67500 E. Rs. 68500

5. A book-shelf contains 2 English, 3 Hindi and 4 Sanskrit books. If two books are picked at random, then what is the probability that either all are Sanskrit or all are English books?

A. [latex]\frac {12}{36}[/latex] B. [latex]\frac {7}{36}[/latex] C. [latex]\frac {15}{36}[/latex] D. [latex]\frac {11}{36}[/latex] E. [latex]\frac {18}{36}[/latex]

Answers and Explanations
1. Answer - Option E
Explanation -
First part amount = (P + 1000)
Second part amount = (P + 1200)
Third part amount = (P - 800)
ATQ-
[latex]\frac {(P + 1200) \times 10 \times 2}{100} - \frac {(P - 800) \times 8 \times 2}{100} = 500[/latex]
[latex]\frac {(P + 1200)}{5} - \frac {(4P-3200)}{25} = 500[/latex]
Solving for P from the equation above:
P = 12500 - 9200 = 3300
Total saving of abhishek = (3300 + 1000) + (3300 + 1200)+ (3300 - 800)
= 11300
Total C.I on his saving at 10% = [latex] 10 + 10 + \frac {10 \times 10}100 [/latex]
= 21%
= [latex]\frac {11300 \times 21}{100} = 2373 [/latex]
2. Answer - Option D
Explanation -
20 men were employed to complete the work in say n days. Therefore, the estimated work 20n man days
Work completed in [latex]\frac {n}{3}[/latex] days is 5n man days.
Remaining time according to revised schedule
= [latex]\frac {3N}{4} - \frac {n}{3} = \frac {9n - 4n}{12} = \frac {5n}{12}[/latex]
Remaining work = 15n man days
20 men in [latex]\frac {n}{3}[/latex] days do 5n man days of work
So, number of men needed in [latex]\frac {5n}{12}[/latex] days to do
15n man days of work = (20) ([latex]\frac {n}{3}[/latex] ) ([latex]\frac {12}{5n}[/latex]) ([latex]\frac {15}{5}[/latex]) = 48
Hence, 28 additional men are needed.
3. Answer - Option A
Explanation -
Let the cost price (CP) of TV = 100
CP of washing machine = 60
What Amit has paid,
Cost of washing machine= 60 × [latex]\frac {75}{100}[/latex] = 45
Cost of TV = 100 × [latex]\frac {90}{100}[/latex] = 90
Total= 90 + 45 = 135
What amit is supoosed to pay
Cost of washing machine= 60 × [latex]\frac {90}{100}[/latex] = 54
Cost of TV= 100 × [latex]\frac {75}{100}[/latex] = 75
Total = 54 + 75 = 129
⸫ required % = [latex] [\frac {(135-129)}{129}]\times 100 [/latex] = 4.65 %
4. Answer - Option C
Explanation -
P : Q : R
[latex]X \times 2 : (x + 8000) \times 1 : (x + 12000) \times 3[/latex]
8 : 6 : 21
ATQ-
= [latex]\frac {2x}{x + 8000} = \frac {8}{6}[/latex]
6x - 4x = 32000
X = 16000
Required sum of capital ( P + Q + R)-
= 16000 + (16000 + 8000) + (16000 + 12000)
=68000
5. Answer - Option B
Explanation -
The number of books = 2 + 3 + 4 = 9
n(S) = [latex]^{9}{C}_{2} = \frac {9 \times 8}{2} = 36[/latex]
n(E) = [latex]^{4}{C}_{2} + ^{2}{C}_{2} = 6 + 1 = 7[/latex]
∴ P(E) = [latex] \frac {n(E)}{n(S)} = \frac {7}{36} [/latex]

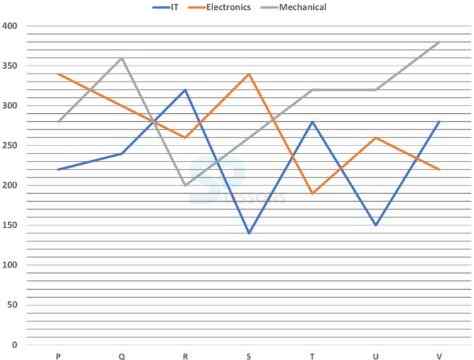
Direction[1-5]: Study the line graph carefully and answer the given questions.
Strength of Seven Technology Institutes with Specializations in IT, Electronics and Mechanical in 2012.

1. If the number of students with Mechanical specialization in each institute increased by 20% and the number of students with IT specialization in each institute decreased by 10% from 2012-13, what is the difference between total mechanical student to total IT student in 2013.

A. 1177 B. 1077 C. 1277 D. 1377 E. 1477

2. What is the ratio between total number of students in institutes R and V respectively?

A. 39 : 43 B. 39 : 44 C. 37 : 44 D. 39 : 45 E. 38 : 43

3. What is the difference between total number of students with Electronics specialization from all the institutes together and the total number of students with Mechanical specialization from all the institutes together?

A. 220 B. 240 C. 280 D. 210 E. 250

4. If the number of students in institutes P, Q and R with IT specialization increased by 15%, 22% and 10% respectively from 2012 to 13, what was the total number of students with IT specialization in the three institutes together in 2013?

A. 1028 B. 1056 C. 898 D. 1142 E. 1145

5. In institutes P, T and U the percentage of girls out of total number of students with Electronics specialization in respective institute is 50%, 55% and 48% respectively, what is the approx total number of boys in these three institutes with Electronics specialization?

A. 391 B. 386 C. 356 D. 360 E. 314

Answers and Explanations
1. Answer - Option B
Explanation -
Total mechanical student = [latex][\frac {(280 + 360 + 200 + 260 + 320 + 320 + 380)}{100}] \times 120 = 2544[/latex]
Total IT student = [latex][\frac {(220 + 240 + 320 + 140 + 280 + 150 + 280)}{100} ]\times 90 = 1467[/latex]
Difference = 2544 - 1467 = 1077
2. Answer - Option B
Explanation -
Total student in R = 200 + 260 + 320 = 780
Total student in V = 220 + 280 + 380 = 880
Ratio = 780 : 880 = 39 : 44
3. Answer - Option D
Explanation -
Total mechanical student = (280 + 360 + 200 + 260 + 320 + 320 + 380) = 2120
Total Electronics student = (340 + 300 + 260 + 340 + 190 + 260 + 220) = 1910
Difference = 2120 – 1910 = 210
4. Answer - Option C
Explanation -
Total number = [latex] [\frac {(220 \times 115)}{100}]+ [\frac {(240 \times 122)}{100}]+ [\frac {(320 \times 110)}{100}] = 898 [/latex]
5. Answer - Option A
Explanation -
Total no. of boys (Approx.) in P, T and U = [latex] [\frac {(340 \times 50)}{100}]+ [\frac {(190 \times 45)}{100}]+ [\frac {(260 \times 52)}{100}] = 391 [/latex]

Direction[1-2]: In the following question two equations are given in variables X and Y. You have to solve these equations and determine the relation between X and Y.
1. I. 3[latex] {X}^{2}[/latex] + 7X = 6 II. 3[latex] {Y}^{2}[/latex] - 7Y + 2 = 0

A. X>Y B. X<Y C. X≥Y D. X≤Y E. X=Y OR No relation can be established(CND)

2. I. 6[latex] {X}^{2}[/latex] - 7X + 2 = 0 II.2[latex] {Y}^{2}[/latex] - 15Y + 25 = 0

A. X>Y B. X<Y C. X≥Y D. X≤Y E. X=Y OR No relation can be established(CND)

Direction[3-4]: What will come in place of the question marks (?) in the following questions?
3. 67.39 -11.78 + 19.63 =? + 22.41

A. 52.73 B. 52.83 C. 65.78 D. 64.78 E. None of these

4. 125 of 44% + 840 of 75% = ?

A. 600 B. 666 C. 685 D. 765 E. None of these

5. A sum was put at simple interest at a certain rate for 2 years. Had it been put at 2 % higher rate, it would have fetched Rs. 400 more. Find the sum.

A. 8000 B. 9000 C. 10000 D. 12000 E. 14000

Answers and Explanations
1. Answer - Option E
Explanation -
3[latex] {X}^{2}[/latex] + 7X = 6
3[latex] {X}^{2}[/latex] + 7X - 6 = 0
3[latex] {X}^{2}[/latex] + 9X - 2X - 6 = 0
3X(X + 3) -2(X + 3) = 0
(X + 3)(3X - 2) = 0
X = -3 or X= [latex] \frac{2}{3}[/latex]
3[latex] {Y}^{2}[/latex] - 7Y + 2 = 0
3[latex] {Y}^{2}[/latex] - 6Y - Y + 2 = 0
3Y(Y - 2) -1(Y - 2) = 0
(Y - 2)(3Y - 1) = 0
Y = 2 or Y = [latex] \frac{1}{3}[/latex]
No relation can be established.
2. Answer - Option B
Explanation -
6[latex] {x}^{2}[/latex] - 7x + 2 = 0
6[latex] {x}^{2}[/latex] - 4x - 3x + 2 = 0
2x(3x - 2)-1(3x - 2) = 0
(3x - 2)(2x - 1) = 0
x = [latex] \frac{2}{3}[/latex] or x = [latex] \frac{1}{2}[/latex]
2[latex] {y}^{2}[/latex] -15y + 25 = 0
2[latex] {y}^{2}[/latex] - 10y - 5y + 25 = 0
2y(y - 5)- 5(y - 5) = 0
(y - 5)(2y - 5) = 0
y = 5 or y = [latex] \frac{5}{2}[/latex]
x<y
3. Answer - Option B
Explanation -
67.39 -11.78 + 19.63 = ? + 22.41
? = 75.24 – 22.41 [latex]\rightarrow[/latex] 52.83
4. Answer - Option C
Explanation -
44% of 125 + 75% of 840 = 55 + 630 = 685
5. Answer - Option C
Explanation -
Let sum be x.
Original rate be R.
1st condition:
Rate of interest = R
Time = 2 years
2nd condition:
Rate of interest increased by 2 = (R + 2) %
Time = 2 years
Therefore,
[latex]\frac {[P × (R + 2) × 2]}{100} - \frac {(P × R × 2)}{100} = 400[/latex]
2PR + 4P - 2PR - = 40000
4P = 40000
P = Rs.10000
The required sum is Rs. 10,000