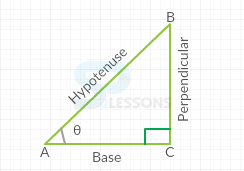
Consider a right angled triangle [latex]\bigtriangleup[/latex] ABC, Where [latex]\angle[/latex]ACB = [latex]\theta[/latex],

1. Sin[latex]\theta[/latex] is equal to ratio between perpendicular and hypotenuse.
2. Cos[latex]\theta[/latex] is equal to ratio between base and hypotenuse.
3. Tan[latex]\theta[/latex] is equal to ratio between perpendicular and base.
4. Cosec[latex]\theta[/latex] is the inverse of sin[latex]\theta[/latex].
5. Sec[latex]\theta[/latex] is the inverse of cos[latex]\theta[/latex].
6. Cot[latex]\theta[/latex] is the inverse of tan[latex]\theta[/latex].
Values of T-ratios:

Angle of elevation:

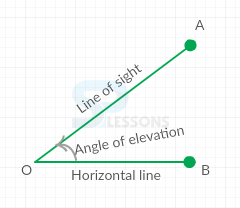
Assume that a person from a point O looks up at an object A, placed above the level of eye. Then, the angle which the line of sight makes with the horizontal through O, is called angle of elevation of A as seen from O.
Therefore, Angle of elevation of A from O = [latex]\angle[/latex]BOD.
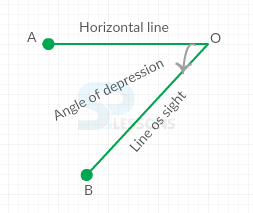
Angle of Depression:

Assume that a person from a point O looks down at an object B, placed below the level of eye, then the angle which the line of sight makes with the horizontal through O, is called the angle of depression of B as seen from O.
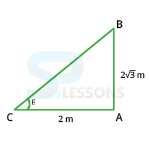
Example 1: If the height of a pole is [latex]2\sqrt{3}[/latex] meters and the length of its shadow is 2 meters, find the angle of elevation of the sun.

Solution:

Let AB be the pole and AC be its shadow.
Let angle of elevation, ∠ ABC = θ.
Then, AB = [latex]2\sqrt{3}[/latex]m, AC = 2m.
tan θ = [latex]\frac{AB}{AC}[/latex] = [latex]\frac{2\sqrt{3}}{2}[/latex] = [latex]\sqrt{3}[/latex]
θ = 60°
So, the angle of elevation is 60°

Example 2: A ladder leaning againt a wall makes an angle of 60° with the ground. If the length of the ladder is 19m, find the distance of the foot of the ladder from the wall.

Solution:

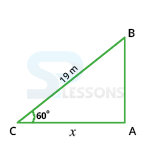
Let AB be the wall and BC be the ladder.
Then, ∠ ABC = 60° and BC = 19 m.
Let AC = x meters
[latex]\frac{AC}{BC}[/latex] = cos 60°
[latex]\frac{x}{19}[/latex] = [latex]\frac{1}{2}[/latex]
[latex]x[/latex] = [latex]\frac{19}{2}[/latex] = 9.5.
Distance of the foot of the ladder from the wall = 9.5 m.

Example 3: The angle of elevation of the top of a tower at a point on the ground is 30°. On walking 24m towards the tower, the angle of elevation becomes 60°. Find the height of the tower.

Solution:

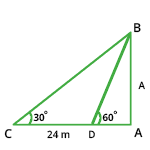
Let AB be the tower and C and D be the points of observation. Then,
[latex]\frac{AB}{AD}[/latex] = tan 60° = [latex]\sqrt{3}[/latex] ⇒ AD = [latex]\frac{AB}{\sqrt{3}}[/latex] = [latex]\frac{h}{3}[/latex]
[latex]\frac{AB}{AC}[/latex] = tan 30° = [latex]\frac{1}{\sqrt{3}}[/latex] ⇒ AC = AB x [latex]\sqrt{3}[/latex] = [latex]h\sqrt{3}[/latex].
CD = (AC - AD) = [latex](h\sqrt{3} - \frac{h}{\sqrt{3}})[/latex]
∴ [latex]h\sqrt{3} - \frac{h}{\sqrt{3}}[/latex] = 24 ⇒ h = [latex]12\sqrt{3}[/latex] = (12 x 1.73) = 20.76.
Hence, the height of the tower is 20.76 m.

From the above triangle [latex]\bigtriangleup[/latex]ACB,
1. [latex]{Hypotenuse}^2[/latex] = [latex]{Base}^2 + {perpendicular}^2[/latex]
2. Sin[latex]\theta[/latex] = [latex]\frac{perpendicular}{hypotenuse}[/latex] = [latex]\frac{CB}{AB}[/latex]
3. Cos[latex]\theta[/latex] = [latex]\frac{base}{hypotenuse}[/latex] = [latex]\frac{AC}{AB}[/latex]
4. Tan[latex]\theta[/latex] = [latex]\frac{perpendicular}{base}[/latex] = [latex]\frac{CB}{AC}[/latex]
5. Cosec[latex]\theta[/latex] = [latex]\frac{1}{sin\theta}[/latex] = [latex]\frac{AB}{CB}[/latex]
6. Sec[latex]\theta[/latex] = [latex]\frac{1}{cos\theta}[/latex] = [latex]\frac{AB}{AC}[/latex]
7. Cot[latex]\theta[/latex] = [latex]\frac{1}{tan\theta}[/latex] = [latex]\frac{AC}{CB}[/latex]
Trig Identities:
1. [latex]sin^2\theta + cos^2\theta[/latex] = 1
2. 1 + [latex]tan^2\theta[/latex] = [latex]sec^2\theta[/latex]
3. 1 + [latex]cot^2\theta[/latex] = [latex]cosec^2\theta[/latex]

1. A man on the top of a tower, standing on the seashore finds that a boat coming towards the man takes 20 minutes for the angle of depression to change from [latex]{30}^{\circ}[/latex] to [latex]{60}^{\circ}[/latex]. Find the time taken by the boat to reach the shore from this position?
Solution:

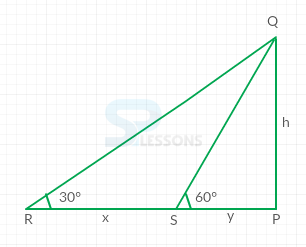
Assume a triangle PQR
Let PQ be the tower and R and S be the two positions of the boat.
Assume PQ = h, RS = [latex]x[/latex] and PS = [latex]y[/latex]



From the figure,
[latex]\frac{h}{y}[/latex] = tan[latex]{60}^{\circ}[/latex] = [latex]\sqrt{3}[/latex]
⇒ [latex]y[/latex] = [latex]\frac{h}{\sqrt{3}}[/latex]
[latex]\frac{h}{x + y}[/latex] = tan[latex]{30}^{\circ}[/latex] = [latex]\frac{1}{\sqrt{3}}[/latex]
⇒ [latex]x + y[/latex] = [latex]\sqrt{3} h[/latex]
Now, [latex]x[/latex] = [latex](x + y) - y [/latex] = ([latex]\sqrt{3}h - \frac{h}{\sqrt{3}}[/latex]) = [latex]\frac{2h}{\sqrt{3}}[/latex]
So, [latex]\frac{2h}{\sqrt{3}}[/latex] is covered in 10 min.
Therefore, [latex]\frac{h}{\sqrt{3}}[/latex] will be covered in (10 x [latex]\frac{\sqrt{3}}{2h}[/latex] x [latex]\frac{h}{\sqrt{3}})[/latex] = 5 min.
Hence, required time = 5 minutes.

2. From a point P on a level ground, the angle of elevation of the top tower is [latex]{30}^{\circ}[/latex]. If the tower is 200 m high, find the distance of point B from the foot of the tower?
Solution:

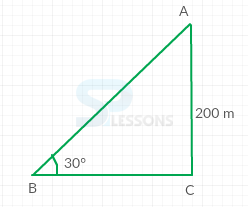
Let us consider a triangle ABC as shown below
Given that,
[latex]\angle[/latex]ABC = [latex]{30}^{\circ}[/latex]
Height (h) = AC = 200 m



From the figure,
tan[latex]{30}^{\circ}[/latex] = [latex]\frac{AC}{BC}[/latex]
⇒ [latex]\frac{1}{\sqrt{3}}[/latex] = [latex]\frac{200}{BC}[/latex]
⇒ BC = 200[latex]\sqrt{3}[/latex] = 200 x 1.73 = 346 m
Therefore, the distance of point B from the foot of the tower = 346 m.

3. Find the angle of elevation of the sun, when the length of the shadow of a tree is equal to the height of the tree?
Solution:

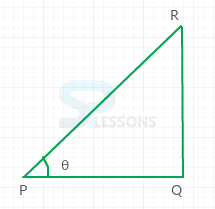
Assume a triangle PQR, as shown below:



Here, PQ = QR
Let [latex]\angle[/latex]QPR = [latex]\theta[/latex]
From the figure,
tan[latex]\theta[/latex] = [latex]\frac{QR}{PQ}[/latex] = 1 (since PQ = QR)
⇒ [latex]\theta[/latex] = [latex]{45}^{\circ}[/latex]
Therefore, angle of elevation = [latex]{45}^{\circ}[/latex]

4. An observer 2 m tall is 10[latex]\sqrt{3}[/latex] m away from a tower. The angle of elevation from his eye to the top of the tower is [latex]{30}^{\circ}[/latex]. Find the height of the tower?
Solution:

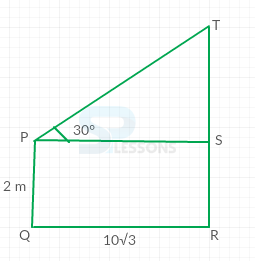
Given that,
AN observer 2 m is 10[latex]\sqrt{3}[/latex] m away from tower
Angle of elevation = [latex]{30}^{\circ}[/latex]
Let us consider the below figure,



From the figure,
SR = PQ = 2m
PS = QR = 10[latex]\sqrt{3}[/latex] m
tan[latex]{30}^{\circ}[/latex] = [latex]\frac{TS}{PS}[/latex]
⇒ [latex]\frac{1}{\sqrt{3}}[/latex] = [latex]\frac{TS}{10\sqrt{3}}[/latex]
⇒ TS = 10m
Now, TR = TS + SR = 10 + 2 = 12m
Therefore, the height of the tower = 12m

5. The angle of elevation of a ladder leaning against a wall is [latex]{60}^{\circ}[/latex] and the foot of the ladder is 12.4 m away from the wall. Find the length of the ladder?
Solution:

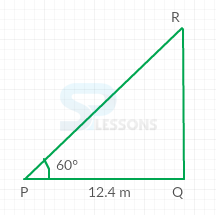
Given that,
The foot of the ladder is 12.4 m away from the wall.
Angle of elevation = [latex]{60}^{\circ}[/latex]
Assume triangle PQR, as shown below:



From the figure,
cos[latex]{60}^{\circ}[/latex] = [latex]\frac{PQ}{PR}[/latex]
⇒ [latex]\frac{1}{2}[/latex] = [latex]\frac{12.4}{PR}[/latex]
⇒ PR = 24.8 m
Therefore, the length of the ladder is 24.8 m