Decimal fractions: Decimal fractions are defined as fractions in which denominators are powers of 10.
Examples:
1. [latex]\frac{1}{10} = 1[/latex] tenth = .1
2. [latex]\frac{1}{100} = 1[/latex] hundredth = .01
3. [latex]\frac{99}{100} = 99[/latex] hundredths = .99
4. [latex]\frac{7}{1000} = 7[/latex] thousandths = .007
Addition & subtraction:
Addition and subtraction is done by placing the given numbers under each other that the decimal points lie in one column.
Example 1: Evaluate: 12.1212 + 101.32 - 306.76 = ? (B.S.R.B, 2003)
Solution:

Given Expression = (12.1212 + 17.0005) - 9.1102 = (29.1217 - 9.1102) = 20.0115.

Example 2: Evaluate: 48.95 - 32.006 (I.B.P.S. 2002)
Solution:

48.95 - 32.006 = 16.944

Example 3: Evaluate: 792.02 + 101.32 - 306.76 (NABARD, 2002)
Solution:

792.02 + 101.32 = 893.34
893.34 - 306.76 = 586.58

Multiplication Multiplication is done by two methods.

• One is by a power of 10 i.e. we need to shift the decimal to the right as many places as in the power of 10.


• Other is by multiplying the given numbers without decimal points and after obtaining the answer put the decimal as sum of the number of decimal places in the given numbers.

Example 1:  Evaluate: 0.002 × 0.5 = ? (Bank P.O 2003)
Solution:

2 x 5 = 10. Sum of decimal places = 4.
∴ 0.002 x 0.5 = 0.0010 = 0.001.

Example 2:  Evaluate: 16.02 x 0.001 = ? (Bank P.O 2002)
Solution:

1602 x 1 = 1602. Sum of decimals places = 5.
∴ 16.02 x 0.001 = 0.000196.

Example 3: Evaluate: 3.14 x [latex]10^{6}[/latex]
Solution:

3.14 x [latex]10^{6}[/latex] = 3.140000 x 1000000 = 3140000.

Division
Division is done by two methods.

• One is by a decimal fraction i.e. we need to multiply both dividend and divisor by power of 10 to make divisor a whole number.


• Other is by dividing the given numbers without decimal points and after obtaining the answer put the decimal as many places of decimal as there are in dividend.

Example 1: Evaluate: [latex]2.5 \div 0.0005[/latex]
Solution:

[latex]\frac{2.5}{0.0005}[/latex] = [latex]\frac{25 \times 10000}{0.0005 \times 10000}[/latex] = [latex]\frac{25000}{5}[/latex] = 5000.

Example 2: Evaluate: [latex]0.006 \div ?[/latex] = 0.6
Solution:

Let [latex]\frac{0.006}{x}[/latex] = 0.6. Then, [latex]x[/latex] = [latex]\frac{0.006}{0.6}[/latex] = [latex]\frac{0.006 \times 10}{0.6 \times 10}[/latex] = [latex]\frac{0.06}{0.6}[/latex] = 0.01.

Example 3:
Evaluate: [latex]? \div .025[/latex] = 80
Solution:

Let [latex]\frac{x}{.025}[/latex] = 80. Then, [latex]x[/latex] = 80 x .025 = 2.

Recurring: Recurring means repeating a figure or a set of figures continuously in a decimal fraction.
Examples:
1. [latex]\frac{5}{6}[/latex] = 0.83333..... = 0.8[latex]\overline{3}[/latex].
2. Express as vulgar fractions: 0.[latex]\overline{37}[/latex] = [latex]\frac{37}{99}[/latex].
3. Express as vulgar fractions: 0.[latex]\overline{053}[/latex] = [latex]\frac{53}{999}[/latex].

Step 1: Divide the decimal by 1, i.e. [latex]\frac{decimal}{1}[/latex]
Step 2: For Every number after the decimal point multiply by 10 for both top and bottom (i.e. if there are two numbers after the decimal point, then use 100, if there are three use 1000)
Step 3: Reduce or simplify the fraction
Example 1: Convert 0.75 to a fraction.
Solution:

Step 1: Divide the 0.75 by 1,
[latex]\frac{0.75}{1}[/latex]
Step 2: Multiply both top and bottom by 100 (because there are 2 digits after the decimal point so that is 10 × 10 = 100)
[latex]\frac{0.75 \times 100}{1 \times 100}[/latex] = [latex]\frac{75}{100}[/latex]
Step 3: Simplify the fraction,
[latex]\frac{75}{100}[/latex] = [latex]\frac{15}{20}[/latex] = [latex]\frac{3}{4}[/latex] (Divide by 5)
Here [latex]\frac{75}{100}[/latex] is called a decimal fraction and [latex]\frac{3}{4}[/latex] is called a common fraction.

Example 2 Convert 0.625 to a fraction
Solution:

Step 1: Divide the 0.625 by 1,
[latex]\frac{0.625}{1}[/latex]
Step 2: Multiply both top and bottom by 100 (because there are 3 digits after the decimal point so that is 10 × 10 x 10 = 1000)
[latex]\frac{0.625 \times 1000}{1 \times 1000}[/latex] = [latex]\frac{625}{1000}[/latex]
Step 3: Simplify the fraction,
[latex]\frac{625}{1000}[/latex] (Divide by 25) = [latex]\frac{25}{40}[/latex] (Divide by 5) = [latex]\frac{5}{8}[/latex]

Example 3 Convert 2.35 to a fraction
Solution:

When there is a whole number part, put the whole number aside and bring it back at the end.
So here, Put the 2 aside and just work on 0.35

Step 1: Divide the 0.35 by 1,
[latex]\frac{0.35}{1}[/latex]
Step 2: Multiply both top and bottom by 100 (because there are 2 digits after the decimal point so that is 10 × 10 = 100)
[latex]\frac{35 \times 100}{1 \times 100}[/latex] = [latex]\frac{35}{100}[/latex]
Step 3: Simplify the fraction,
[latex]\frac{35}{100}[/latex] = [latex]\frac{7}{20}[/latex] (Divide by 5)
Bring back 2 to make a mixed fraction : 2 [latex]\frac{7}{20}[/latex]

Comparison is the arrangement of given fractions in ascending order and descending order. so first we need to convert the given fractions into decimal numbers and then it is easy to arrange them accordingly.
Example 1 Arrange the fractions [latex]\frac{1}{2}; \frac{3}{4}; \frac{5}{6}[/latex] in ascending order?
Solution:

by converting, 0.5; 0.75; 0.833
Ascending order is 0.833 > 0.75 > 0.5
Therefore, [latex]\frac{5}{6} >\frac{3}{4} >\frac{1}{2}[/latex].

Example 2 Arrange the fractions [latex]\frac{3}{5}; \frac{4}{7}; \frac{8}{9} and \frac{9}{11}[/latex] in their descending order. (R,.B.I 2003)
Solution:

Clearly, [latex]\frac{3}{5}[/latex] = 0.5, [latex]\frac{4}{7}[/latex] = 0.571, [latex]\frac{8}{9}[/latex] = 0.88, [latex]\frac{8}{11}[/latex] = 0.818.
Now, 0.88 > 0.818 > 0.6 > 0.571.
∴ [latex]\frac{8}{9}[/latex], [latex]\frac{9}{11}[/latex], [latex]\frac{3}{5}[/latex], [latex]\frac{4}{7}[/latex]

.
Example 3 Arrange the fractions [latex]\frac{5}{8}; \frac{7}{12}; \frac{13}{16}, \frac{16}{29} and \frac{3}{4}[/latex] in Ascending order of magnitude.
Solution:

Converting each of the given fractions into decimal form, we get:
[latex]\frac{5}{8}[/latex] = 0.625, [latex]\frac{7}{12}[/latex] = 0.5833, [latex]\frac{13}{16}[/latex] = 0.8125, [latex]\frac{16}{29}[/latex] = 0.5517 and [latex]\frac{3}{4}[/latex] = 0.75.
Now, 0.5517 < 0.5833 < 0.625 < 0.75 < 0.8125.
∴ [latex]\frac{16}{29}[/latex] < [latex]\frac{7}{12}[/latex] < [latex]\frac{5}{8}[/latex] < [latex]\frac{3}{4}[/latex] < [latex]\frac{13}{16}[/latex].

Explanation: This is the first formula in geometry and algebra of mathematics.

Introduction to Geometrical Approach:

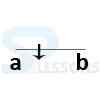
• Line with a point = a+b
  
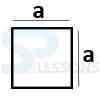
• Square Area = [latex]a^{2}[/latex]
  
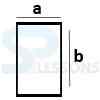
• Rectangle Area = ab
  

Prove [latex](a+b)^2 = a^2 + b^2 +2ab[/latex] in geomentry:

• Draw a line with a point which divides a, b
  
• Total distance of this line = a+b
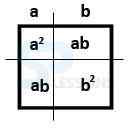
• Now find out the square of a+b ie. [latex](a+b)^{2}[/latex]
  
• The above diagram represents – a + b is a line and the square are is [latex]a^{2}[/latex] + [latex]b^{2}[/latex] + 2ab

Hence proved [latex](a+b)^{2}[/latex] = [latex]a^{2}[/latex] + [latex]b^{2}[/latex] + 2ab
Prove [latex](a+b)^2 = a^2 + b^2 +2ab[/latex] in Algebra:
[latex](a+b)^{2}[/latex] = (a+b)*(a+b)
= (a*a + a*b) + (b*a + b*b)
= ([latex]a^{2}[/latex] + ab) + (ba + [latex]b^{2}[/latex])
= [latex]a^{2}[/latex] + 2ab + [latex]b^{2}[/latex]
Hence proved [latex](a+b)^{2}[/latex] = [latex]a^{2}[/latex] + [latex]b^{2}[/latex] + 2ab

Example 1:
Expand the term [latex](3x + 4y)^{2}[/latex] using the identity [latex](a+b)^{2}[/latex] = [latex]a^{2}[/latex] + [latex]b^{2}[/latex] + 2ab
Solution:

[latex](3x + 4y)^{2}[/latex] = [latex](3x)^{2}[/latex] + [latex](4y)^{2}[/latex] + 2(3x)(4y) = [latex]9x^{2}[/latex] + [latex]16y^{2}[/latex] + 24xy
∴ [latex](3x + 4y)^{2}[/latex] = [latex]9x^{2}[/latex] + [latex]16y^{2}[/latex] + 24xy

Example 2:
Expand the term [latex](\sqrt{2}x + 4y)^{2}[/latex] using the identity [latex](a+b)^{2}[/latex] = [latex]a^{2}[/latex] + [latex]b^{2}[/latex] + 2ab
Solution:

[latex](\sqrt{2}x + 4y)^{2}[/latex] = [latex](\sqrt{2}x)^{2}[/latex] + [latex](4y)^{2}[/latex] + 2[latex](\sqrt{2}x)[/latex](4y) = [latex]2x^{2}[/latex] + [latex]16y^{2}[/latex] + 8[latex]\sqrt{2}[/latex]xy
∴ [latex](\sqrt{2}x + 4y)^{2}[/latex] = [latex]2x^{2}[/latex] + [latex]16y^{2}[/latex] + 8[latex]\sqrt{2}[/latex]xy

Example 3:
Expand the term [latex](x + \frac{1}{x})^{2}[/latex] using the identity [latex](a+b)^{2}[/latex] = [latex]a^{2}[/latex] + [latex]b^{2}[/latex] + 2ab
Solution:

[latex](x + \frac{1}{x})^{2}[/latex] = [latex]x^{2}[/latex] + [latex]\frac{1}{x^{2}}[/latex] + 2[latex](x)(\frac{1}{x})[/latex] = [latex]x^{2}[/latex] + [latex]\frac{1}{x^{2}}[/latex] + 2
∴ [latex](x + \frac{1}{x})^{2}[/latex] = [latex]x^{2}[/latex] + [latex]\frac{1}{x^{2}}[/latex] + 2

[latex]a^2 - b^2 = (a + b)(a - b)[/latex]

[latex](a + b)^2 = a^2 + b^2 + 2ab[/latex]

[latex](a - b)^2 = a^2 + b^2 - 2ab[/latex]

[latex](a + b + c)^2 = a^2 + b^2 + c^2 + 2(ab + bc + ca)[/latex]

[latex](a^3 + b^3) = (a + b)(a^2 - ab + b^2)[/latex]

[latex](a^3 - b^3) = (a-b)(a^2 + ab + b^2)[/latex]

[latex](a^3 + b^3 + c^3 - 3abc) = (a + b + c)(a^2 + b^2 + c^2 - ab - bc - ca)[/latex]

[latex](a^3 + b^3 + c^3) = 3abc when a + b + c = 0[/latex]

1. If 52416 is divided by 312, the quotient is 168. Then what will be the quotient if 52.416 is divided by 0.0168 ?
Solution:

Given that [latex]\frac{52416}{312} = 168[/latex]
or it can also be written as [latex]\frac{52416}{312}[/latex]=312
given that  [latex]\frac{52.416}{0.0168}[/latex]
⇒[latex]\frac{524160}{168}[/latex]
⇒ [latex]\frac{52416}{168}[/latex] × 10
⇒ 312 × 10 = 3120
Therefore the quotient = 3120

2. Find the unknown number from 654.485 + 16.42 + ? = 936.5489
Solution:

Take the unknown number as [latex]"x"[/latex]
by placing [latex]"x"[/latex] in the given equation,
⇒654.485 + 16.42 + [latex] x [/latex] = 936.5489
⇒670.905 + [latex] x [/latex] = 936.5489
⇒[latex] x [/latex] = 936.5489 - 670.905
Therefore [latex] x [/latex] = 265.6439

3. Calculate [latex]\frac{125.36}{25.6}[/latex]?
Solution:

Given that [latex]\frac{125.36}{25.6}[/latex]
multiply both dividend and divisor by power of 10 i.e.
⇒[latex]\frac{12536 × 10}{256 × 10}[/latex]
⇒[latex]\frac{125360}{2560} [/latex] = 48.96
Therefore, [latex]\frac{125.36}{25.6}[/latex] = 48.96

4. Find the descending order of [latex]\frac{15}{3}; \frac{6}{10}; \frac{2}{7}; \frac{4}{11}[/latex]?
Solution:

Given that [latex]\frac{15}{3}; \frac{6}{10}; \frac{2}{7}; \frac{4}{11}[/latex]
Now, fractions are converted into decimals i.e.
[latex]\frac{15}{3}[/latex] = 5
[latex]\frac{6}{10}[/latex] = 0.6
[latex]\frac{2}{7}[/latex] = 0.28
[latex]\frac{4}{11}[/latex] = 0.36
0.28 < 0.36 < 0.6 < 5
Therefore, descending order is [latex]\frac{2}{7}; \frac{4}{11}; \frac{6}{10}; \frac{15}{3}[/latex]

5. Convert the decimals 0.625, 0.8125, 0.5833, 0.75 into simple form of fractions?
Solution:

Given decimals are 0.625, 0.8125, 0.5833, 0.75
0.625 = [latex]\frac{625}{1000} = \frac{5}{8}[/latex]
0.8125 = [latex]\frac{8125}{10000} = \frac{13}{16}[/latex]
0.5833 = [latex]\frac{5833}{10000} = \frac{7}{12}[/latex]
0.75 = [latex]\frac{75}{100} = \frac{3}{4}[/latex]