Introduction
Introduction
Co-ordinate Geometry is an arrangement of geometry where the position of points on the plane is represented using an ordered pair of numbers. Points are placed on the "coordinate plane" as shown below:
From the figure,
x-axis is the horizontal line.
y-axis is the vertical line.
x-axis and y-axis together are known as the co-ordinate axis.
Origin is the point of intersection of these two axis.
Quantitative Aptitude -BANKING|SSC|RAILWAYS|INSURANCE|RECRUITMENT EXAMS - EBOOKS
 Methods
Methods
Signs of co-ordinate in the four quadrants:
- x and y co-ordinates are positive in I quadrant.
- x co-ordinate is negative and y co-ordinate is positive in II quadrant.
- x and y co-ordinate are negative in III quadrant.
- x co-ordinate is positive and y co-ordinate is negative in IV quadrant
Note:
1. (0, 0) are the co-ordinates of origin.
2. On x-axis, the y co-ordinate of any point is 0.
3. On y-axis, the x co-ordinate of any point is 0.
Let any two points on the plane be A([latex]x_{1}, y_{1}[/latex]) and B([latex]x_{2}, y_{2}[/latex]).Then the distance between A and B is represented as AB i.e. given by
AB = [latex]\sqrt{(x_{2} - x_{1})^2 + (y_{2} - y_{1})^2}[/latex]
The distance of the point A(x, y) from the origin (0, 0) is given by
[latex]\sqrt{x^2 + y^2}[/latex]
Internal division:
The co-ordinates of the point P which divides the line joining AB internally in the ratio m: n are
[[latex]\frac{mx_{2} + nx_{1}}{m + n}[/latex], [latex]\frac{my_{2} + ny_{1}}{m + n}[/latex]]
Here, A and B are two points i.e. A([latex]x_{1}, y_{1}[/latex]) and B([latex]x_{2}, y_{2}[/latex]).
External division:
The co-ordinates of the point P which divides the line joining points A([latex]x_{1}, y_{1}[/latex]) and B([latex]x_{2}, y_{2}[/latex]) externally in the ratio m: n are
[[latex]\frac{mx_{2} + nx_{1}}{m + n}[/latex], [latex]\frac{my_{2} + ny_{1}}{m + n}[/latex]]
Here, the point P is beyond A and B for external division and it can be either close to B or close to A.
Mid point:
If P is the mid point and A([latex]x_{1}, y_{1}[/latex]) & B([latex]x_{2}, y_{2}[/latex]) are the two points given then m: n = 1: 1 i.e. m = n.
Therefore, the co-ordinates or the point P are given by
([latex]\frac{x_{1} + x_{2}}{2}[/latex], [latex]\frac{y_{1} + y_{2}}{2}[/latex])
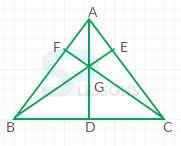
Centroid:
Here, from the above figure,
G is the centroid.
A = ([latex]x_{1}, y_{1}[/latex])
B = ([latex]x_{2}, y_{2}[/latex])
C = ([latex]x_{3}, y_{3}[/latex])
If A, B and C are the vertices of a triangle. The three medians of the triangle intersect at its centroid and the centroid divides the median in the ratio 2 : 1.
Co-ordinates of the point G are given by
([latex]\frac{x_{1} + x_{2} + x_{3}}{3}[/latex], [latex]\frac{y_{1} + y_{2} + y_{3}}{3}[/latex])
Straight line:
- A straight line is represented as a linear equation of the first degree in two variables x and y.
- ax + by + c = 0 is the general form of equation of a line.
- How steeply that line climbs or falls as it moves from left to right is a measurement of a line slope.
- If there are two points on a line, once again ([latex]x_{1}, y_{1}[/latex]) and then the slope of that line can be determined using the formula i.e. Slope = [latex]\frac{y_{2} - y_{1}}{x_{2} - x_{1}}[/latex]
- A linear equation of the first degree in two variables x and y represents a straight line.
- The equation is ax + by + c = 0
 Formula
Formula
1. AB = [latex]\sqrt{(x_{2} - x_{1})^2 + (y_{2} - y_{1})^2}[/latex]
2. The distance of the point A(x, y) from the origin (0, 0) is given by
[latex]\sqrt{x^2 + y^2}[/latex]
3. The co-ordinates of the point P which divides the line joining AB internally in the ratio m: n are
[[latex]\frac{mx_{2} + nx_{1}}{m + n}[/latex], [latex]\frac{my_{2} + ny_{1}}{m + n}[/latex]]
4. The co-ordinates of the point P which divides the line joining points A([latex]x_{1}, y_{1}[/latex]) and B([latex]x_{2}, y_{2}[/latex]) externally in the ratio m: n are
[[latex]\frac{mx_{2} + nx_{1}}{m + n}[/latex], [latex]\frac{my_{2} + ny_{1}}{m + n}[/latex]]
5. The co-ordinates or the point P are given by
([latex]\frac{x_{1} + x_{2}}{2}[/latex], [latex]\frac{y_{1} + y_{2}}{2}[/latex])
6. Co-ordinates of the point G are given by
([latex]\frac{x_{1} + x_{2} + x_{3}}{3}[/latex], [latex]\frac{y_{1} + y_{2} + y_{3}}{3}[/latex])
7. Slope = [latex]\frac{y_{2} - y_{1}}{x_{2} - x_{1}}[/latex]
8. y = mx + c
9. ([latex]y - y_{1}[/latex]) = [latex]\frac{y_{2} - y_{1}}{x_{2} - x_{1}}(x - x_{1}[/latex])
10. ([latex]y - y_{1}[/latex]) = m[latex](x - x_{1}[/latex])
11. [latex]\frac{x}{a} + \frac{y}{b}[/latex] = 1
 Samples
Samples
1. Find the perimeter of the triangle connecting the points with (x, y) co-ordinates (-2, 7), (3, -5) and (-2, -5)?
Solution:
A. The quantity on the left is greater.
B. The quantity on the right is greater.
C. Both are equal.
D. The relationship cannot be determined without further information.
Solution:
A. The quantity on the left is greater.
B. The quantity on the right is greater.
C. Both are equal.
D. The relationship cannot be determined without further information.
Solution:
A. The quantity on the left is greater.
B. The quantity on the right is greater.
C. Both are equal.
D. The relationship cannot be determined without further information.
Solution:
- The points A, B and C form a right triangle ACB, by sketching it on a graph.
Given that
A = (-2, 7)
B = (3, -5)
C = (-2, -5)
Now, calculate the lengths of the three sides and add them together to get the perimeter i.e.
Length of AC = 7(-5) = 12
Length of BC = 3-(-2) = 5
Using Pythagorean theorem,
[latex](AB)^2[/latex] = 12 x 12 + 5 x 5
AB = 13
Therefore, perimeter = 12 + 13 + 5 = 30
- Given that,
5x + 4y + 6 = 0
P([latex]x_{1}, y_{1}[/latex]) = (2, 3)
Equation to the line passing through the point ([latex]x_{1}, y_{1}[/latex])) and perpendicular to the line ax + by + c = 0 is
b([latex]x - x_{1}[/latex]) + a([latex]y - y_{1}[/latex]) = 0
4(x - 2) + 5(y - 3) = 0
4x + 5y - 23 = 0
Therefore, the required line is 4x + 5y - 23 = 0
| Quantity A | Quantity B |
| The slope of the line | The y-intercept of the line |
- The given equation is in slope-intercept form, so slope is the co-efficient of the x-term and the y-intercept is the term without a variable.
Here,
The slope is 3.
The y-intercept is 2.
Thus, the slope is the greater quantity.
Hence, correct option is A.
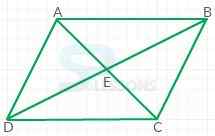
| Quantity A | Quantity B |
| The length of line segment EB | The length of line segment AB |
- The diagonals of a rhombus are perpendicular to each other.
So, angles AEB and CEB are both right angles.
Thus, AEB is a right triangle.
Hypotenuse of triangle is line segment AB because it is opposite the right angle.
Line segment EB is also part of the same triangle, opposite one of the smaller angles of the triangle.
Therefore, the longest of the three sides of a triangle is hypotenuse always.
So, line segment AB is longer.
Hence, right answer is option B.
| Quantity A | Quantity B |
| The distance between the points with rectangular coordinates (0,5) and (0,10) | The distance between the points with rectangular coordinates (1,8) and (-3,5) |
- Both points are on the y-axis, and are 5 units apart.
The line joining the points on the right hand side forms the hypotenuse of a triangle with sides 4 (parallel to the x-axis), and 3 (parallel to the y-axis).
This means the hypotenuse must be 5 (3-4-5 triangle).
So both columns are equal.
Hence, option C is right answer.