Alligation: It is a rule which defines the proportion/ratio in which two or more ingredients at given prices must be mixed to produce a mixture of  a desired/specified price.
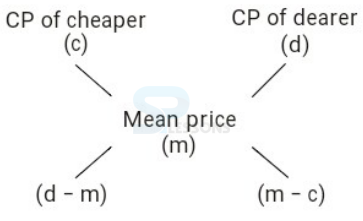
Mean price: The cost price of a unit quantity of the mixture is termed as mean price.

The above relation is represented as,

Hence, [latex]\frac{Quantity \ of \ cheaper}{Quantity \ of \ dearer}[/latex] = (d - m) : (m - c) = [latex]\frac{d - m}{m - c}[/latex]
Alligation rule is also used to fins the ratio in which two or more ingredients at their respective prices should be mixed to produce a mixture at a given price.
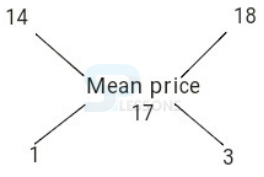
Example In what proportion must tea at Rs. 14 per kg be mixed with tea at Rs. 18 per kg, so that the mixture be worth Rs. 17 a kg?
Solution:

Cp of 1 kg cheaper tea CP of 1 kg dearer tea



[latex]\frac{Quantity \ of \ cheaper}{Quantity \ of \ dearer}[/latex] = [latex]\frac{18 - 17}{17 - 14}[/latex] = [latex]\frac{1}{3}[/latex] = 1 : 3

Example There are two containers of equal capacity. The ratio of milk to water in the first container is 3 : 1, in the second container is 5 : 2. If they are mixed up, then the ratio of milk to water in the mixture will be?
Solution:

Part of milk in first container = [latex]\frac{3}{3 + 1}[/latex] = [latex]\frac{3}{4}[/latex]
Part of water in first container = [latex]\frac{1}{3 + 1}[/latex] = [latex]\frac{1}{4}[/latex]
Similarly, part of milk in second container = [latex]\frac{5}{5 + 2}[/latex] = [latex]\frac{5}{7}[/latex]
Part of water in second container = [latex]\frac{2}{5 + 2}[/latex] = [latex]\frac{2}{7}[/latex]
Therefore, Required = [latex]\frac{3}{4}[/latex] + [latex]\frac{5}{7}[/latex] : [latex]\frac{1}{4}[/latex] + [latex]\frac{2}{7}[/latex] = [latex]\frac{41}{28}[/latex] : [latex]\frac{15}{28}[/latex] = 41 : 15

Example A container contains 40 liters of milk. From this container 4 liters of milk was taken out and replaced by waster. This process was repeated further two times. How much milk is now contained by the container?
Solution:

Amount of milk left after 3 operations
= [40[latex](1 - \frac{4}{40})^{3}[/latex]] liters = (40 x [latex]\frac{9}{10}[/latex] x [latex]\frac{9}{10}[/latex] x [latex]\frac{9}{10}[/latex]) = 29.16 liters.

1. Alligation rule:

[latex] \frac{Quantity \ of \ cheaper}{Quantity \ of \ dearer} [/latex] = [latex] \frac{(Cost \ price \ of \ dearer) - (Mean \ price)}{(Mean \ price) - (Cost \ price \ of \ cheaper)} [/latex]
(or)
Quantity of cheaper : Quantity of dearer = (Cost price of dearer - Mean price) : (Cost price of cheaper) (\( x - z) : (z - y \))

2. Suppose a container contains \( x \) units of liquid from which \( y \) units are taken out and replaced by water. After \( n \) operations, the quantity of pure liquid = [\( x (1 - \frac{y}{x})^n \)] units

1. The milk and water in two vessels S and T are in the ratio 4 : 7 and 2 : 3 respectively. In what ratio, the liquids in both the vessels be mixed to obtain a new mixture in vessel U containing [latex]\frac{1}{2}[/latex] milk and [latex]\frac{1}{2}[/latex] water?
Solution:

Given,
Ratio of milk and water in vessel S = 4 : 7
Ratio of milk and water in vessel T = 2 : 3
Let cost price of milk be Rs. 1 litre
Milk in 1 litre mixture of S = [latex]\frac{4}{7}[/latex] litre
Milk in 1 litre mixture of T = [latex]\frac{2}{5}[/latex] litre
Milk in 1 litre mixture of U = [latex]\frac{1}{2}[/latex] litre
Therefore,
Cost price of 1 litre mixture in S = Rs. [latex]\frac{4}{7}[/latex]
Cost price of 1 litre mixture in T = Rs. [latex]\frac{2}{5}[/latex]
Mean price = Rs. [latex]\frac{1}{2}[/latex]
By the rule of alligation,
Required ratio = [latex] \frac{2}{5} - \frac{1}{2} : \frac{1}{2} - \frac{4}{7}[/latex]
⇒ [latex] \frac{1}{10} : \frac{1}{14}[/latex]
⇒ 7 : 5

2. A man travelled a distance of 80 km in 7 hours partly on foot at the rate of 8 km per hour and partly on bicycle at 16 kmph. Find the distance travelled on foot?
Solution:

Given,
Distance travelled in one hour on foot = 8 km
Distance travelled in one hour on bicycle = 16 km
Average in one hour = [latex] \frac{80}{7} [/latex]
By rule of alligation,
[latex] \frac{Time taken by foot}{Time taken on bicycle}[/latex] = [latex] \frac{32}{24} [/latex] = [latex] \frac{4}{3} [/latex]
Thus, out of 7 hours in all, the man took 4 hours to travel on foot.
Therefore, Distance covered on foot in 4 hours.

3. How many kilograms of dearer sugar costing Rs. 5.75 per kilogram be mixed with 75 kilogram of cheaper sugar costing Rs. 4.50 per kilogram so that the mixture is worth Rs. 5.50 per kilogram?
Solution:

Given,
Cost price of 1 kilogram of cheaper suger = Rs. 4.50
Cost price of 1 kilogram dearer sugar = Rs. 5.75
Mean price = Rs. 5.50
Quantity of cheaper sugar = 75 kilogram
Here, Rs. 5.75 - Rs. 5.50 = Rs. 0.25
Rs. 5.50 - Rs. 4.50 = Rs. 1.00
Therefore, required ratio is
[latex]\frac{Quantity of cheaper sugar}{Quantity of dearer sugar}[/latex] = [latex]\frac{0.25}{1}[/latex] = [latex]\frac{1}{4}[/latex]
⇒ [latex]\frac{75}{Quantity of dearer sugar}[/latex] = [latex]\frac{1}{4}[/latex]
⇒ Quantity of dearer sugar = 75 x 4 = 300 kilograms
Therefore, Quantity of dearer sugar = 300 kilograms

4. How much water must be added to 60 litres at 1[latex]\frac{1}{2}[/latex] litres for Rs. 20 so as to have a mixture worth Rs. 10[latex]\frac{2}{3}[/latex] a litre?
Solution:

Given,
Cost price of 1 litre of water = 0
Cost price of 1 litre of milk = Rs. [latex] \frac{40}{3} [/latex]
Mean price = Rs. [latex]\frac{32}{3}[/latex]
Here, [latex]\frac{40}{3} - \frac{32}{3}[/latex] = [latex]\frac{8}{3}[/latex]
Therefore, required ratio of water and milk = [latex]\frac{8}{3} : \frac{32}{3}[/latex] = 8 : 32 = 1 : 4.
Therefore, Quantity of water to be added to 60 litres of milk = [latex] \frac{1}{4} [/latex] x 60 litres = 15
litres

5. A goldsmith has two qualities of gold, one of 10 carats and another of 15 carats purity. In what proportion should mix both to make an ornament of 12 carats purity?
Solution:

Given,
One quality of gold = 10 carats
Another quality of gold = 15 carats
By alligation rule,
Required ratio = 15 - 12 : 12 - 10 = 3 : 2