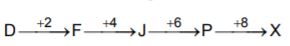Introduction
Introduction
RRB has released Notification for Railway JE 2019 Exam. The entire recruitment process of RRB JE 2019 Exam shall involve, CBT - I, CBT - II and Document Verification/ Medical Examination as applicable. The 1st stage CBT is of screening nature and the standard of questions for the CBT will be generally in conformity with the educational standards and/or minimum technical qualifications prescribed for the posts. The normalized score of 1st stage exam shall be used only for short listing of candidates for 2nd stage exam as per their merit. The article RRB JE CBT 1 Practice Paper provides basic idea questions asked in each topic. [latex]{1}^{st}[/latex] STAGE CBT (Common for all Notified Posts).
The RRB JE CBT 1 Exam will be divided into four sections- Mathematics, General Science, General Awareness and General Intelligence and Reasoning. There will be 1/3rd of negative marking.
 Quiz
Quiz
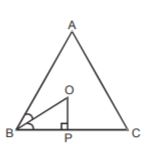
1. Ratio of the time taken by A alone to complete a certain piece of work while that by B and C to complete the same work together is 4 : 3. If the time taken by C to complete the work alone is 8 days and the ratio of the efficiencies of B and C is 1 : 3, then find the time in which A and B can complete the work while working together.
- A. 4.5 days
B. 6 days
C. 7.5 days
D. 8 days
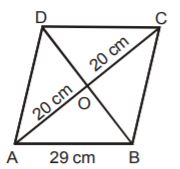
- A. 840 [latex]{cm}^{2}[/latex]
B. 880 [latex]{cm}^{2}[/latex]
C. 820 [latex]{cm}^{2}[/latex]
D. 800 [latex]{cm}^{2}[/latex]
- A. 38.5 %
B. 41.5 %
C. 39.8 %
D. 40.5 %
- A. Rs. 1,020
B. Rs. 1,428
C. Rs. 1,462
D. Rs. 1,468
- A. 20 %
B. 16.67 %
C. 25 %
D. 33.33 %
- A. 5.26%
B. 4.16%
C. 4.28%
D. 4.46%
- A. 11.4 sec
B. 10.4 sec
C. 11.64 sec
D. 10.64 sec
- A. 8 : 15
B. 24 : 7
C. 12 : 5
D. 6 : 8
- A. 0
B. [latex]{sec}^{2} A[/latex]
C. 1
D. 2
- A. 20°
B. 160°
C. 140°
D. 40°
- A. 0
B. 1
C. 2
D. 3
- A. [latex]\frac{3}{4}[/latex]
B. [latex]- \frac{3}{4}[/latex]
C. [latex] \frac{3}{5}[/latex]
D. [latex]- \frac{3}{5}[/latex]
- A. 58 years
B. 78 years
C. 68 years
D. 76 years
- A. 2
B. -1
C. 1
D. 0
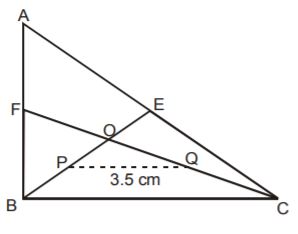
- A. 3.5 cm
B. 7 cm
C. 10.5 cm
D. 4.5 cm
- A. 9 : 4
B. 9 : 25
C. 16 : 25
D. 9 : 16
- A. 5 %
B. 6 %
C. 7 %
D. 8 %
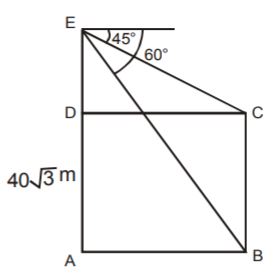
- A. [latex]20 \sqrt{3} [/latex]
B. [latex]20 \sqrt{2} [/latex]
C. [latex]40 \sqrt{2} [/latex]
D. 8.6 m
- A. Rs. 22, 450
B. Rs. 21, 600
C. Rs. 17, 000
D. Rs. 19, 600
- A. 7:00 p.m.
B. 7:30 p.m.
C. 8:00 p.m.
D. 8:30 p.m.
- A. 10
B. 6
C. 5
D. 3
- A. [latex]\frac{31}{110}[/latex]
B. [latex]\frac{31}{101}[/latex]
C. [latex]\frac{41}{101}[/latex]
D. [latex]\frac{3}{11}[/latex]
- A. -4
B. -1
C. 0
D. [latex]\frac{2}{17}[/latex]
- A. 39°
B. 78°
C. 51°
D. 102°
- A. 9
B. 10
C. 11
D. Both (a) and (c)
- A. 22 minutes
B. 10 minutes
C. 6 minutes
D. 5 minutes
- A. 12
B. 6
C. 18
D. 24
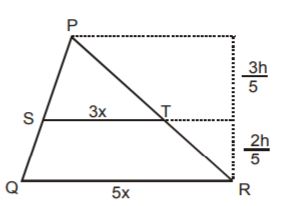
- A. 12 cm
B. 15 cm
C. 24 cm
D. 27 cm
- A. Rs. 210
B. Rs. 240
C. Rs. 280
D. Rs. 300
- A. 100 Km
B. 120 Km
C. 140 km
D. 160 km
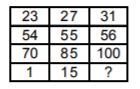
1. A series is given, with one term missing. Choose the correct alternative from the given ones that will
complete the series.
DNP, ELS, FJV, ___?__
- A. GHZ
B. HHY
C. GIW
D. GHY
- A. 110
B. 113
C. 118
D. 115
- A. Daughter-in-law
B. Sister-in-law
C. Mother
D. Sister
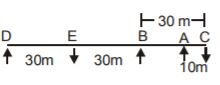
- A. 40 m
B. 30 m
C. 60 m
D. 50 m
- A. 44
B. 24
C. 43
D. 34
- A. 5
B. 9
C. 12
D. 20
- A. 243
B. 423
C. 324
D. 432
- A. 37
B. 30
C. 29
D. 130
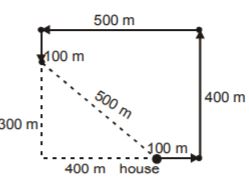
- A. 400 m
B. 500 m
C. 300 m
D. 600 m
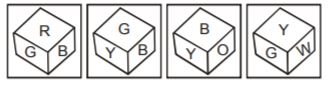
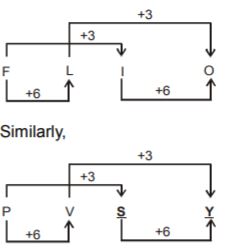
- A. B
B. Y
C. O
D. W
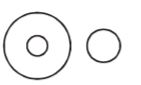
- A.
B.
C.
D.
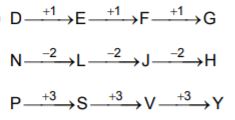
- A. R-Y
B. S-X
C. S-Y
D. R-W
- A. Kitten
B. Kid
C. Joey
D. Fawn
- A. bbab
B. bcab
C. abac
D. acab
- A. French Beans
B. Gourd
C. Pumpkin
D. Jack fruit
- A. 325
B. 118
C. 272
D. 253
- A. Solar energy
B. Biomass
C. Fossil fuel
D. Radiant energy
- A. Man
B. Whale
C. Hen
D. Seal
- A. Anil
B. Sunil
C. Mukesh
D. Karan
- A. B D G J P
B. C E I O V
C. D F J P X
D. E G K P X
- A. 33
B. 25
C. 28
D. 29
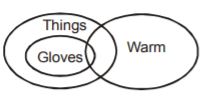
- I. All gloves are things.
II. Some gloves are warm.
- I. All gloves are warm.
II. All warm are things.
III. Some warm are things
- A. Only conclusion III follows
B. Only conclusion I follows
C. Only conclusion II follows
D. None follows
- People succeed when they work hard
- I. Only hard work leads to success.
II. Honesty does not lead to success.
- A. Only conclusion I follows
B. Only conclusion II follows
C. Both conclusions I and II follow
D. Neither conclusion I nor II follows
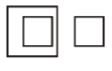
- A.
B.
C.
D.
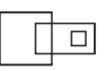
- A.
B.
C.
D.
1. The first Indian foreign policy was formulated by:
- A. Dr Bhimrao Ambedkar
B. Pt. Jawaharlal Nehru
C. Indira Gandhi
D. Babu Jagjivan Ram
- A. 6
B. 9
C. 11
D. 15
- A. Kalibanga
B. Lotha
C. Banawali
D. Ropar
- A. Rajgriha
B. Pataliputra
C. Kundalgrama
D. Vaishali
- A. Enclaves
B. Edge Cities
C. Primate Cities
D. World Class Cities
- A. Agra
B. Karachi
C. Kabul
D. Lahore
- A. A.R.Rehman
B. Sushmit Sen
C. Vishwa Mohan Bhatt
D. Ehsaan Noorani
- A. Goods Exported
B. Goods Imported
C. Goods Safe for Environment
D. Only processed food
- A. Odisha
B. Madhya Pradesh
C. Chhattisgarh
D. Jharkhand
- A. Red Soil
B. Late-rite Soil
C. Black Soil
D. Alluvial Soil
- A. Ajay Srivastava
B. Pradeep Kumar
C. Ranjit Srivastava
D. Pankuj Sharma
- A. Cathryn Lorraine Fitzpatrick
B. Jhulan Goswami
C. Betty Wilson
D. Diana Edulji
- A. Keep Cool and Carry On: The Montreal Protocol
B. Protect Ozone layer for future generations
C. Unite for the protection of Ozone layer
D. No to pollutants and save to Ozone layer
- A. 140
B. 138
C. 150
D. 128
- A. Kendrick Lamar
B. Caroline Shaw
C. Kevin Puts
D. Henry Threadgill
1. The disadvantages of liquid propellants are
- A. Difficult to store and handle
B. Extreme toxicity
C. Moderately cryogenic
D. All of these
- A. antibody A and B both are present in AB blood group
B. no antigen is present in AB blood group
C. antigen A and B both are present in AB blood group
D.
- A. Ammonia
B. Nitric acid
C. Hydrogen peroxide
D. Sulphuric acid
- A. NAND gate
B. AND gate
C. XOR gate
D. OR gate
- A. Air pollution
B. Soil erosion
C. Water pollution
D. Marine pollution
- A. Retina
B. Pupil
C. Sclera
D. Cornea
- A. Kyoto protocol
B. Montreal protocol
C. Stockholm Convention on Persistent Organic Pollutants
D. Protocol to the Convention on Long-range Trans boundary Air Pollution on the Control of Emissions of Volatile Organic Compounds
- A. Fat coating
B. Sugar coating
C. Protein coating
D. Glyco protein coating
- A. Dendrology
B. Dendrochronology
C. Chronology
D. Acanthochronology
- A. Vampyronassa
B. Cladoselache
C. Archaeopteryx
D. Rhyniognatha
- A. Agar-Agar
B. Algal extract
C. Algal bloom
D. Algal excreta
- A. Energy pyramid
B. Pyramid of numbers
C. Ecological pyramid of biomass
D. All of these
- A. Rennin
B. Renin-angiotensin
C. Thyroid
D. Parathyroid
- A. Virus
B. Bacteria
C. Nematode
D. Protozoan
- A. Haustorium
B. Vellum
C. Prop roots
D. Pneumatophore
- A. Osteology
B. Archaeology
C. Opthalmology
D. Otolaryngology
- A. Lux seconds
B. Candela
C. Roentgen
D. Decibels
- A. Ultra violet radiations
B. Infra red radiations
C. Visible spectrum
D. Ions present in the stratosphere
- A. Ants
B. Queen bees
C. Worker bees
D. Drones
- A. Neon
B. Helium
C. Nitro-us oxide
D. MIC
- A. Ethylene
B. Methane
C. Propane
D. Butane
- A. Tube Light
B. Solar Cell
C. Candle
D. Dynamo
- A. Lichens
B. Algae
C. Mosses
D. Ferns
- A. Granite
B. Basalt
C. Obsidian
D. Limestone
- A. Sodium benzoate
B. Diclofenac
C. Azadirachtin
D. Sodium thiopental
- A. extreme shining in diamond
B. Looming
C. Mirage
D. All of the above
- A. Coma
B. Croma
C. Nebula
D. Parabola
- A. Oxidation
B. Reduction
C. Hydrogenation
D. Decrease in viscosity
- A. Measles
B. Mumps
C. Botulism
D. Poliomyelitis
- A. Refrigeration
B. Sugaring
C. Pickling
D. Drying