Introduction
GRE General Test Quantitative Reasoning is primarily categorized into the below-mentioned topics. The GRE Multiple Choice Select One Answer category assesses the basic mathematical skills, understanding of the elementary mathematical concepts and ability to quantitatively reason and to model and solve problems with quantitative methods. GRE Multiple Choice Select One Answer questions are multiple-choice questions that ask to select only one answer choice from a list of five choices.
This article provides the detail information about the GRE Multiple Choice Select One Answer of GRE General Test.
- Arithmetic- The topics include properties and types of integers, such as divisibility, factorization, prime numbers, remainders and odd and even integers; arithmetic operations, exponents and roots; and concepts such as estimation, percent, ratio, rate, absolute value, the number line, decimal representation and sequences of numbers.
- Algebra- The topics include operations with exponents; factoring and simplifying algebraic expressions; relations, functions, equations and inequalities; solving linear and quadratic equations and inequalities; solving simultaneous equations and inequalities; setting up equations to solve word problems; and coordinate geometry, including graphs of functions, equations and inequalities, intercepts and slopes of lines.
- Geometry- The topics include parallel and perpendicular lines, circles, triangles - including isosceles, equilateral and 30°-60°-90° triangles - quadrilaterals, other polygons, congruent and similar figures, three-dimensional figures, area, perimeter, volume, the Pythagorean theorem and angle measurement in degrees. The ability to construct proofs is not tested.
- Data analysis- The topics include basic descriptive statistics, such as mean, median, mode, range, standard deviation, interquartile range, quartiles and percentiles; interpretation of data in tables and graphs, such as line graphs, bar graphs, circle graphs, boxplots, scatterplots and frequency distributions; elementary probability, such as probabilities of compound events and independent events; conditional probability; random variables and probability distributions, including normal distributions; and counting methods, such as combinations, permutations and Venn diagrams. These topics are typically taught in high school algebra courses or introductory statistics courses. Inferential statistics is not tested.
-
✦ Quantitative Comparisons
✦ Single-Answer Multiple-Choice
✦ Multiple-Answer Multiple-Choice
✦ Numeric Entry
✦ Data Interpretation
Tips for MC
GRE Multiple Choice Select One Answer - Tips
- Use the fact that the answer is there. If the answer is not one of the five answer choices given, test takers should assume that the answer is incorrect and do the following:
- Reread the question carefully – test takers may have missed an important detail or misinterpreted some information.
- Check the computations – test takers may have made a mistake, such as mis-keying a number on the calculator.
- Reevaluate the solution method – test takers may have a flaw in the reasoning.
- Examine the answer choices. In some questions, test takers are asked explicitly which of the choices has a certain property. You may have to consider each choice separately or you may be able to see a relationship between the choices that will help test takers find the answer more quickly. In other questions, it may be helpful to work backward from the choices, say, by substituting the choices in an equation or inequality to see which one works. However, be careful, as that method may take more time than using reasoning.
- For questions that require approximations, scan the answer choices to see how close an approximation is needed. In other questions, too, it may be helpful to scan the choices briefly before solving the problem to get a better sense of what the question is asking. If computations are involved in the solution, it may be necessary to carry out all computations exactly and round only test takers final answer in order to get the required degree of accuracy. In other questions, test takers may find that estimation is sufficient and will help to avoid spending time on long computations.
Samples
Directions: Select a single answer choice.
Question 1:
If 5x + 32 = 4 - 2x what is the value of x?
The figure above shows the graph of the function f, defined by f(x) = |2x|+ 4 for all numbers x. For which of the following functions g, defined for all numbers x, does the graph of g intersect the graph of f?
It is clear that this line will not intersect the graph of f to the left of the y-axis. To the right of the y-axis, the graph of f is a line with slope 2, which is greater than slope 1. Consequently, as the value of x increases, the value of y increases faster for f than for g, and therefore the graphs do not intersect to the right of the y-axis. Choice B is similarly ruled out. Note that if the y-intercept of either of the lines in Choices A and B were greater than or equal to 4 instead of less than 4, they would intersect the graph off.
Choices C and D are lines with slope 2 and y-intercepts less than 4. Hence, they are parallel to the graph of f (to the right of the y-axis) and therefore will not intersect it. Any line with a slope greater than 2 and a y-intercept less than 4, like the line in Choice E, will intersect the graph of f (to the right of the y-axis).The correct answer is Choice E, g(x) = 3x – 2.
-
A. - 4
B. - 3
C. 4
D. 7
E. 12
-
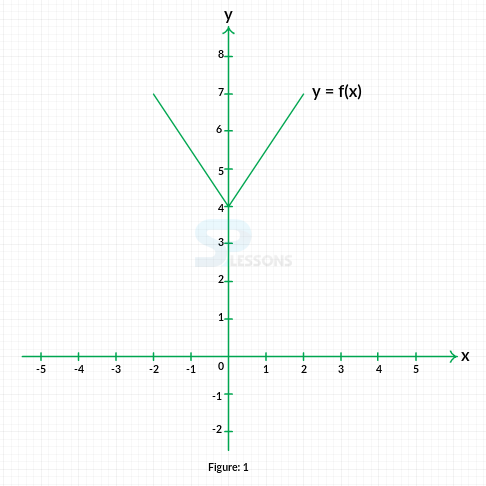
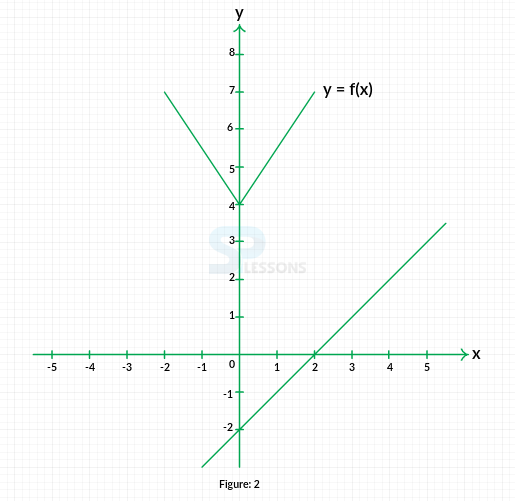
A. g(x) = x - 2
B. g(x) = x + 3
C. g(x) = 2x -2
D. g(x) = 2x + 3
E. g(x) = 3x - 2