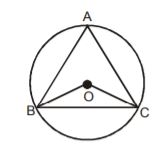
1. The circumcentre of a triangle is always the point of intersection of the

A. Medians B. Perpendiculars bisectors C. Altitude bisector D. Perpendiculars dropped from the vertices on the opposite sides of the triangle

Answer - Option B
Explanation -
Circumcentre of a triangle is the point of intersection of perpendicular bisectors of its sides.
2. The Qutab Minar casts a shadow 150 m long at the same time when the Vikas Minar casts a shadow of 120 m long on the ground. If the height of the Vikas Minar is 80 m, then the height of the Qutab Minar is

A. 180 m B. 100 m C. 150 m D. 120 m

Answer - Option B
Explanation -
Let height of Qutab Minar be x metres
[latex]\frac{150}{120}[/latex] = [latex]\frac{x}{80}[/latex]
x = [latex]\frac{150 * 80}{120}[/latex] = 100
3. The number of tangents that can be drawn to two non-intersecting circles is

A. 4 B. 3 C. 2 D. 1

Answer - Option A
Explanation -
Hence 4 tangents can be drawn.
4. An angle is equal to 1/3 rd of its supplement. Find its measure

A. 60º B. 80º C. 90º D. 45º

Answer - Option D
Explanation -
Let the angle be xº
i.e, x = [latex]\frac{1}{3} * (180 – x)[/latex]
Hence x = 45º
5. A man goes 10 m due east and then 24 m due north. Find the distance from the starting point.

A. 26 m B. 24 m C. 28 m D. 30 m

Answer - Option A
Explanation -
6. The sum of the interior angles of a polygon is 1620º. The number of sides of the polygon are

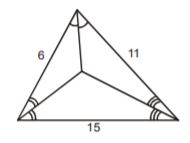
A. 9 B. 11 C. 15 D. 12

Answer - Option B
Explanation -
Sum of the interior angles of a polygon of n sides
= [latex] (2n – 4) * \frac{\pi}{2}[/latex]
i.e, [latex] (2n – 4) * \frac{\pi}{2}[/latex] = [latex] (1620) * \frac{\pi}{180}[/latex]
n – 2 = 9
n = 11
7. How many sides a regular polygon has with its interior angle eight times its exterior angle?

A. 16 B. 24 C. 18 D.

Answer - Option C
Explanation -
Let n be the number of sides of the polygon.
i.e, Interior angle = 8 * Exterior angle
[latex]\frac{}{}[/latex] = 8 * [latex]\frac{(2n – 4) * \frac{\pi}{2}}{n}[/latex]
n – 2 = 16
n = 18
8. If [latex]\frac{5 \pi}{6}[/latex] is the measure of each interior angle of a regular convex polygon, then it must be a

A. octagon B. hexagon C. dodecagon D. pentagon

Answer - Option C
Explanation - [latex]\frac{5 \pi}{6}[/latex] = 150º
Exterior angle = 30º
i.e, Number of sides = [latex]\frac{360º}{Exterior angle}[/latex]
[latex]\frac{360º}{30º}[/latex] = 12
9. I n a quadrilateral ABCD, ∠B = 90º and [latex]A{D}^{2} = A{B}^{2} + B{C}^{2} + C{D}^{2}[/latex], then ∠ACD is equal to

A. 90º B. 60º C. 30º D. None of theseº

Answer - Option A
Explanation -
[latex]A{D}^{2} = A{B}^{2} + B{C}^{2} + C{D}^{2}[/latex]
[latex]= A{C}^{2} + C{D}^{2}[/latex]
∠ACD = 90º
10. In a triangle ABC, ∠A = xº, ∠B = yº and ∠C = (y + 20)º. If 4x – y = 10, then the triangle is

A. Right-angled B. Obtuse-angled C. Equilateral D. None of these

Answer - Option A
Explanation -
x + y + (y + 20) = 180
x + 2y = 160 (i)
and 4x – y = 10 (ii)
Solving (i) and (ii) we get
y = 70, x = 20
Hence the angles of the triangle are 20º, 70º, 90º
Thus, the triangle is right angled
11. The perimeters of two similar triangle ABC and PQR ar e 36 cm and 24 cm respectively. If PQ = 10 cm, then the length of AB is

A. 16 m B. 12 m C. 14 m D. 15 m

Answer - Option D
Explanation -
[latex]\frac{AB}{PQ}[/latex] = [latex]\frac{36}{24}[/latex]
AB = [latex]\frac{3}{2}[/latex]
PQ = [latex]\frac{3}{2} * 10[/latex] = 15
12. In the following figure, find ∠ADC.

A. 55 B. 27 .5 C. 60 D. 30

Answer - Option B
Explanation -
AB = BC
∠BAC = ∠BCA = [latex]\frac{110º}{2}[/latex] = 55º
∠ACD = 125º
Also, AC = CD
∠CAD = ∠ADC = [latex]\frac{55º}{2}[/latex] = 27.5º
13. Two isosceles triangles have equal vertical angles and their areas are in the ratio 9 : 16. The ratio of their corresponding heights is

A. 3 : 4 B. 4 : 3 C. 2 : 1 D. 1 : 2

Answer - Option A
Explanation -
Given triangles are congruent.
i.e, [latex]\frac{Area of {1}^{st} triangle}{Area of {2}^{nd}triangle =} = \frac{{{h}^{2}}_{1}}{{{h}^{2}}_{2}}[/latex]
[latex]\frac{{{h}^{2}}_{1}}{{{h}^{2}}_{2}} = \frac{9}{16}[/latex]
[latex]\frac{{h}_{1}}{{h}_{2}}[/latex][latex]\frac{3}{4}[/latex]
14. A 25 m long ladder is placed against a vertical wall inside a room such that the foot of the ladder is 7 m from the foot of the wall. If the top of the ladder slides 4 m downwards, then the foot of the ladder will slide by

A. 2 m B. 4 m C. 8 m D. 16 m

Answer - Option C
Explanation -
AB = 25
BC = 24
B'C = 20
A'B' = 25
'A C' = 15
'A A' = 8 m
15. The area of a field in the shape of a trapezium measures 1440 m. The perpendicular distance between its parallel sides is 24 m. I f the ratio of the parallel sides is 5 : 3, the length of the longer parallel side is

A. 45 m B. 60 m C. 75 m D. 120 m

Answer - Option C
Explanation -
Area of trapezium
= [latex]\frac{1}{2}[/latex] (sum of parallel sides) × height
= [latex]\frac{1}{2}[/latex] (5x + 3x) × 24 = 1440.
Solving, we get x = 15
and length of longer side = 5 × 15 = 75

1. Suppose it is 3 o’clock. After 20 minutes the angle between the smaller and bigger hands will be

A. 20º B. 30º C. 110º D. 120º

Answer - Option A
Explanation -
Degrees at 3 : 20
= 5 min distance – [latex]\frac{1}{3}[/latex] (5 min) distance
= 30 – 10 = 20 degrees
2. The radius of the circumcircle of an equilateral triangle of side 12 cm is

A. [latex]\frac{4}{3} \sqrt{3}[/latex] cm B. 4 [latex]\sqrt{3} [/latex] cm C. 4 [latex]\sqrt{2} [/latex] D. [latex]\frac{4}{3} \sqrt{2}[/latex] cm

Answer - Option B
Explanation - Circumcentre of a triangle is the point of intersection of the right bisectors of its sides

i.e, sin60º = [latex]\frac{QM}{QC}[/latex]
[latex]\frac{\sqrt{3}}{2}[/latex] = [latex]\frac{6}{QC}[/latex]
QC = [latex]\frac{6 * 2}{\sqrt{3}} = 4 \sqrt{3}[/latex] cm
3. If the perimeter of an isosceles right triangle is(6 + 3[latex]\sqrt{2} [/latex]) m, then the area of the triangle is

A. 4.5 [latex]{m}^{2}[/latex] B. 5.4 [latex]{m}^{2}[/latex] C. 9 [latex]{m}^{2}[/latex] D. 81 [latex]{m}^{2}[/latex]

Answer - Option A
Explanation -
Perimeter = (6 + 3[latex]\sqrt{2} [/latex]) m
i.e, x + x + [latex]\sqrt{2} x = 6 + 3\sqrt{2} [/latex]
2x + [latex]\sqrt{2} x = 6 + 3\sqrt{2} [/latex]
x = [latex]\frac{6 + 3\sqrt{2}}{2 + \sqrt{2}}[/latex] = [latex]\frac{3(2 + \sqrt{2})}{2 + \sqrt{2}}[/latex]
= 3
i.e, Required area of triangle
[latex]\frac{1}{2}[/latex] * x * x = [latex]\frac{1}{2} {x}^{2}[/latex]
[latex]\frac{1}{2} * {3}^{2}[/latex] = 4.5 [latex]{m}^{2}[/latex]
4. If two diameters of a circle intersect each other at right angles, then the quadrilateral formed by joining their end points is a

A. Rhombus B. Rectangle C. Square D. Parallelogram

Answer - Option C
5. Of all the chords of a circle passing through a given point in it, the smallest is that which

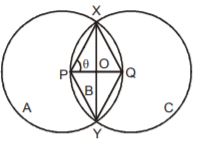
A. is trisected at the point B. is bisected at the point C. passes through the center D. none of these

Answer - Option D
6. I n a tr iangle ABC, t he lengths of the sides AB, AC and BC are 3, 5 and 6 cm respectively. If a point D on BC is drawn such that the line AD bisects the angle A internally, then what is the length of BD?

A. 2 cm B. 2.25 cm C. 2.5 cm D. 3 cm

Answer - Option B
Explanation -
i.e, Divide BC = 6 in the ratio 3 : 5
Thus BD = [latex]6 \frac{3}{3 + 5}[/latex] = [latex]\frac{9}{4}[/latex] = 2.25 cm
7. With the vertices of a △ABC as centers, three circles are described each touching the other two externally. If the sides of the triangle are 4, 6 and 8 cm respectively, then the sum of the radii of the three circles equals

A. 10 B. 14 C. 12 D.

Answer -9 Option D
Explanation -
AB = [latex]{r}_{1} + {r}_{2}[/latex] = 4
BC = [latex]{r}_{2} + {r}_{3}[/latex] = 6
CA = [latex]{r}_{3} + {r}_{1}[/latex] = 8
i.e, 2[latex]({r}_{1} + {r}_{2}+ {r}_{3})[/latex] = 4 + 6 +8
[latex]({r}_{1} + {r}_{2}+ {r}_{3})[/latex] = 9
8. In the figure given below, O is the center of the circle. If ∠OBC = 37º, the ∠BAC is equal to

A. 74 B. 106 C. 53 D. 37

Answer - Option C
Explanation -
∠OBC = 37º
OB = OC = radius
i.e, ∠OCB = ∠OBC = 37º
i.e, ∠BOC = 180º – (37º + 37º) = 106º
Now, ∠BAC = [latex]\frac{1}{2}[/latex] ∠BOC = [latex]\frac{1}{2}[/latex] * 106 = 53º
9. If, in the following figure, PA = 8 cm, PD = 4 cm, CD = 3 cm, then AB is equal to

A. 3.0 cm B. 3.5 cm C. 4.0 cm D. 4.5 cm

Answer - Option D
Explanation -
From the given figure,
PC * PD = PA * PB
i.e, (4 + 3) * 4 = 8 * PB
PB = [latex]\frac{28}{8}[/latex] = 3.5 cm
i.e, AB = AP – BP = 8 – 3.5
= 4.5 cm
10. Two circles of unit radius touch each other and each of them touches internally a circle of radius two, as shown in the following figure. The radius of the circle which touches all the three circles is

A. 5 B. [latex]\frac{3}{2}[/latex] C. [latex]\frac{2}{3}[/latex] D. None of these

Answer - Option C
Explanation -
[latex]O{C}_{1} = 1, O{C}_{1} = r + 1[/latex]
OC = AC – AO = CD – AO,
[AC and CD are radius of the bigger circle]
i.e, OC = 2 – r
[latex]{O{C}_{1}}^{2} = {O{C}_{1}}^{2} + {OC}^{2}[/latex]
[latex]{r + 1}^{2} = 12 + {(2 -r)}^{2}[/latex]
[latex]{r}^{2} + 2r + 1 = 1 + 4 - 4r + {r)}^{2}[/latex]
6r = 4
r = [latex]\frac{4}{6}[/latex] = [latex]\frac{2}{3}[/latex]
11. The two sides of a right triangle containing the right angle measure 3 cm and 4 cm. The radius of the incircle of the triangle is

A. 3.5 cm B. 1.75 cm C. 1 cm D. 0.875 cm

Answer - Option C
Explanation -
If incircle of a triangle ABC touches BC at D,then
|BC - CD| = |AB - AC|
In our case, AC = 5, AB = 3

AC – AB = 2
i.e, CD – BD = 2
In our case, BC = 4
BD + DC = 4 and – BD + DC = 2
CD = 3
BD = 1 = OE
= Radius of the incircle
12. If P and Q are the mid points of the sides CA and CB respectively of a triangle ABC, right-angled at C. Then the value of 4 ([latex]A{Q}^{2} + B{P}^{2}[/latex]) is equal to

A. 4 ([latex]B{C}^{2}[/latex] B. 5 ([latex]A{B}^{2}[/latex] C. 2 ([latex]A{C}^{2}[/latex] D. 2 ([latex]B{C}^{2}[/latex]

Answer - Option B
Explanation -
[latex]A{Q}^{2} = A{C}^{2} + Q{C}^{2}[/latex]
[latex]B{P}^{2} = B{C}^{2} + C{P}^{2}[/latex]
[latex]A{Q}^{2} + B{P}^{2} = (A{C}^{2} + Q{C}^{2}) + (B{C}^{2} + C{P}^{2})[/latex]
=[latex]A{B}^{2} + P{Q}^{2}[/latex]
= [latex]A{B}^{2} ({AB \frac{1}{2}})^{2}[/latex]
(i.e, [latex]AB \frac{1}{2}[/latex])
= [latex]A{B}^{2}\frac{5}{4}[/latex]
= [latex]4(A{Q}^{2} + B{P}^{2}) = 5A{B}^{2}[/latex]
13. If one of the diagonals of a rhombus is equal to its side, then diagonals of the rhombus are in the ratio

A. [latex]\sqrt{3} [/latex] : 1 B. [latex]\sqrt{2} [/latex] : 1 C. 3 : 1 D. 2 : 1

Answer - Option A
Explanation -
Area of a rhombus = [latex]\frac{1}{2}[/latex](product of their diagnonals)
= [latex]\frac{1}{2}[/latex]xy
Again, Area of a rhombus = 2 * Area of equilateral triangle ABD

= 2 * [latex]\frac{\sqrt{3}}{4}{x}^{2}[/latex]
= [latex]\frac{\sqrt{3}}{2}{x}^{2}[/latex]
From (i) and (ii), we have
[latex]\frac{1}{2}[/latex]xy = [latex]\frac{\sqrt{3}}{2}{x}^{2}[/latex]
[latex]\frac{y}{x} = \frac{\sqrt{3}}{1}[/latex]
y : x = [latex]\sqrt{3}[/latex] : 1
14. If the sides of a right tringle are x, x + 1 and x – 1, then the hypotenuse is

A. 5 B. 4 C. 1 D. 0

Answer - Option A
Explanation -
Let (x + 1) be the hypotenuse
i.e, [latex]{(x + 1)}^{2} = {x}^{2} + {(x + 1)}^{2}[/latex]
[latex]{x}^{2} + 2x + 1 = {x}^{2} + {x}^{2} - 2x + 1[/latex]
[latex]{x}^{2} - 4x = 0[/latex]
x(x + 4) = 0
x = 4, as x ≠ 0
i.e, Hypotenuse = 4 + 1 = 5
15. ABCD is a square, F is mid point of AB and E is a point on BC such that BE is one-third of BC. If area of △FBE = 108 [latex]{m}^{2}[/latex], then the length of AC is

A. 63 m B. 36 [latex]\sqrt{2}[/latex] m C. 63 [latex]\sqrt{2} [/latex] m D. 72 [latex]\sqrt{2} [/latex] m

Answer - Option B
Explanation -
Let the side of the square be 6K
i.e, [latex]\frac{1}{2}[/latex] * 3K * 2K = 108
K = 6
i.e, Side of the square = 36m
[latex]A{C}^{2} = C{D}^{2} + D{C}^{2}[/latex]
[latex] = {36}^{2} + {36}^{2}[/latex]
= 2 * [latex] = {36}^{2}[/latex]
AC = 36 [latex]\sqrt{2}[/latex] m

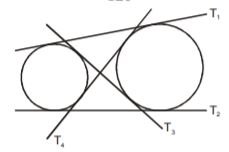
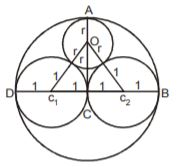
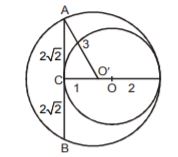
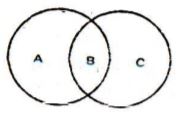
1. Two circles touch each other internally. Their radii are 2 cm and 3 cm. The biggest chord of the outer circle which is outside the inner circle is of length

A. 2 [latex]\sqrt{2}[/latex] cm B. 3 [latex]\sqrt{2} [/latex] m C. 2 [latex]\sqrt{3} [/latex] cm D. 4 [latex]\sqrt{2} [/latex] m

Answer - Option D
Explanation -
AB is the chord of the outer circle touching the inner circle.
2. The product of the lengths of three sides of a triangle is 196 cm and the radius of its circumcircle is 2.5 cm. The area of the triangle is

A. 39.2 [latex]{cm}^{2}[/latex] B. 19.6 [latex]{cm}^{2}[/latex] C. 122.5 [latex]{cm}^{2}[/latex] D. 61.25 [latex]{cm}^{2}[/latex]

Answer - Option B
Explanation -
If a, b, c are three sides of a triangle and R is radius of its circumcircle, then
△ = Area of the triangle
[latex]\frac{abc}{4R}[/latex] = [latex]\frac{196}{4 * 2.5}[/latex] = 19.6 [latex]{cm}^{2}[/latex]
3. In the figure below, if the perimeter of △ABC is p, then the perimeter of the regular hexagon is

A. [latex]\frac{3p}{\sqrt{2}}[/latex] B. [latex]\frac{\sqrt{2}p}{3}[/latex] C. [latex]\frac{\sqrt{3}p}{2}[/latex] D. [latex]\frac{2p}{\sqrt{3}}[/latex]

Answer - Option D
Explanation -
Let a be the side of the regular hexagon
Let ED ⊥ AC
i.e, AD = [latex]\frac{p}{6}[/latex] = CD
From △ADE, [latex]\frac{AD}{AE}[/latex] = cos 30º
[latex]\frac{\frac{p}{6}}{a}[/latex] = [latex]\frac{\sqrt{3}}{2}[/latex]
6a = [latex]\frac{2p}{\sqrt{3}}[/latex]
i.e, Perimeter of regular hexagon = [latex]\frac{2p}{\sqrt{3}}[/latex]
4. The area of a rhombus is 2016 sq cm and its side is 65 cm. The lengths of the diagonals (in cm) respectively are

A. 125, 35 B. 126, 32 C. 132, 26 D. 135, 25

Answer - Option B
Explanation -
Area = [latex]\frac{1}{2}[/latex] * (Product of the diagonals) = 2016
[latex]\frac{1}{2}[/latex] (2x * 2y) = 2016
xy = 1008
[latex]{x}^{2} + {y}^{2} = {65}^{2} = 4225 [/latex]
[latex]{(x - y)}^{2} = {x}^{2} + {y}^{2} - 2xy[/latex]
= 4225 – 2016 = 2209
i.e, x – y = 47 ...(i)
Now [latex]{(x + y)}^{2} = {(x - y)}^{2} + 2xy[/latex] = 6241
x + y = 79 ...(ii)
Solving (i) and (ii) we get
i.e, x = 63, y = 16
Thus, diagonals are 126 and 32
5. Two circles with radii ‘a’ and ‘b’ respectively touch each other externally. Let ‘c’ be the radius of a circle that touches these two circles as well as a common tangent to the two circles. Then

A. [latex]\frac{1}{\sqrt{a}}[/latex] - [latex]\frac{1}{\sqrt{b}}[/latex] = [latex]\frac{1}{\sqrt{c}}[/latex] B. [latex]\frac{1}{\sqrt{b}}[/latex] - [latex]\frac{1}{\sqrt{a}}[/latex] = [latex]\frac{1}{\sqrt{c}}[/latex] C. [latex]\frac{1}{\sqrt{a}}[/latex] + [latex]\frac{1}{\sqrt{b}}[/latex] = [latex]\frac{1}{\sqrt{c}}[/latex] D. None of these

Answer - Option C
Explanation -
PR = MC = [latex] \sqrt {A{C}^{2} - A{M}^{2}} [/latex]
[latex]\sqrt{{(a + c)}^{2} - {(a - c)}^{2}} = 2 \sqrt{ac} [/latex]
Similarly QR = [latex]2 \sqrt{bc} [/latex]
Now, PQ = PR + RQ
[latex]2 \sqrt{ac} + 2 \sqrt{bc} [/latex]
Draw PN parallel to AB
i.e, PN = AB = a + b,
QN = BQ – BN = b – a
i.e, [latex]P{Q}^{2} = P{N}^{2} - Q{N}^{2}[/latex]
= [latex]{(a + b)}^{2} - {(a - b)}^{2} = 4ab[/latex]
PQ = 2 [latex]\sqrt{ab} [/latex] ...(ii)
From (i) and (ii), we have
[latex]2 \sqrt{ac} + 2 \sqrt{bc} = 2 \sqrt{ab} [/latex]
Dividing it by [latex]2 \sqrt{abc}[/latex] , we get
[latex]\frac{1}{\sqrt{b}} + \frac{1}{\sqrt{a}} = \frac{1}{\sqrt{c}}[/latex]
6. A rhombus OABC is drawn inside a circle whose centre is at O in such a way that the vertices A, B and C of the rhombus are on the circle. If the area of the rhombus is 32 [latex]\sqrt{3} [/latex] m2 , then radius of the circle is

A. 64 m B. 8 m C. 32 m D. 46 m

Answer - Option B
Explanation -
Let AC = 2x, OB = 2y
i.e, Radius = OC = 2y = OB
From △ODC
[latex]O{C}^{2} = O{D}^{2} + C{D}^{2}[/latex]
[latex]{4y}^{2} = {y}^{2} + {x}^{2}[/latex]
[latex]{x}^{2} = {3y}^{2}[/latex]
x = [latex]\sqrt{3}y[/latex]
Also area of the △ODC = [latex]\frac{1}{4}[/latex] * Area of the rhombus OABC
= [latex]\frac{1}{2} * x * y = \frac{1}{4} * 32 \sqrt{3} [/latex]
xy = 16 [latex]\sqrt{3} [/latex] ...(ii)
From (i) and (ii), we have
y = 4, x = 4 [latex]\sqrt{3} [/latex]
i.e, Radius of the circle = 2y = 8
7. The sides of a triangle are 6 cm, 11 cm and 15cm. The radius of its incircle is

A. [latex]\frac{5 \sqrt{2}}{4}[/latex] B. [latex]3 \sqrt{2}[/latex] C. [latex]6 \sqrt{2}[/latex] D. [latex]\frac{4 \sqrt{2}}{5}[/latex]

Answer - Option A
Explanation -
Incentre of a triangle is the point of intersection of the bisectors of its angles.
If r is radius of the incircle, then
r = [latex]\frac{△}{s}[/latex]
where △ = area
s = semi-perimeter of the triangle ABC.
Here, 2s = 6 + 11 + 15 = 32
s = 16
△ = [latex]\sqrt{16(16 - 6)(16 - 11)(16 - 15)} [/latex]
= [latex]\sqrt{16 * 10 * 5 * 1} = 20 \sqrt{2} [/latex]
r = [latex]\frac{20 \sqrt{2} }{16}[/latex] = [latex]\frac{5 \sqrt{2} }{4}[/latex] cm
8. In th e giv en diagr am , two circles pass through each other’s centre. If the radius of each circle is 2, then what is the perimeter of the region marked B ?

A. [latex](\frac{8}{3})\pi[/latex] B. [latex](\frac{4}{5})\pi[/latex] C. [latex]4 \pi[/latex] D. [latex](\frac{5}{3})\pi[/latex]

Answer - Option A
Explanation -
PQ = 2 (Radius of the circle)
PX = PY = QX = QY = 2
(Being radii of circles)
Hence PYQX is a rhombus.
i.e, Thus PO = 1 = OQ
[i.e, Diagonal of a rhombus bisect each other]
cosθ = [latex]\frac{QP}{PX}[/latex] = [latex]\frac{1}{2}[/latex]
θ = 60º
∠XPY = 120º
Arc XQY = [latex]\frac{Circumference * 120º}{360º}[/latex]
[latex]\frac{2 \pi * r}{3}[/latex] = [latex]\frac{2 \pi * 2}{3} = \frac{4 \pi}{3}[/latex]
Similarly, Arc XPY = [latex]\frac{4 \pi}{3}[/latex]
i.e, Required perimeter = [latex]\frac{8 \pi}{3}[/latex]