1. Former Australian captain Mark Taylor has had several nicknames over his playing career. Which of the following was NOT one of them?

A. Tubby B. Stodge C. Helium Bat D. Stumpy

Answer - Option D
Explanation - He was christened 'Helium Bat' very early in his career by team mates, due to his habit of lifting his bat over his shoulder and letting anything bowled outside the off-stump go by.
2. Which was the 1st non Test playing country to beat India in an international match?

A. Canada B. Sri Lanka C. Zimbabwe D. East Africa

Answer - Option B
Explanation - Sri Lanka got the status of Test playing country in 1981, and beat India in the 1979 World Cup. Before this they were champion of ICC non-test playing countries.
3. Which county did Ravi Shastri play for?

A. Glamorgan B. Leicestershire C. Gloucestershire D. Lancashire

Answer - Option A
Explanation - Ravi Shastri once hit spinner Tilak Raj for 6 sixes in an over in a First Class match.
4. Who is the first Indian woman to win an Asian Games gold in 400m run?

A. M.L.Valsamma B. P.T.Usha C. Kamaljit Sandhu D. K.Malleshwari

Answer - Option C
5. Kathakali' is a folk dance prevalent in which state?

A. Karnataka B. Orissa C. Kerala D. Manipur

Answer - Option C
6. Which of the following dances is a solo dance?

A. Ottan Thullal B. Kuchipudi C. Yakshagana D. Odissi

Answer - Option A
7. The National Anthem was first sung in the year

A. 1911 B. 1913 C. 1936 D. 1935

Answer - Option A
Explanation -
8. Madhubani', a style of folk paintings, is popular in which of the following states in India?

A. Uttar Pradesh B. Rajasthan C. Madhya Pradesh D. Bihar

Answer - Option D
9. Light travels at the fastest speed in

A. glass B. water C.hydrogen D. vacuum

Answer - Option D
10. Of the four locations mentioned below the highest inside temperature will be attained in the pressure cooker operated with the pressure valve open

A. at sea level B. at the top of Mt. Everest C. At a place in a valley below sea level D. in an aeroplane flying at a height of 10,000 m with inside pressure maintained at the sea level

Answer - Option C
11. Railway tracks are banked on curves

A. necessary centrifugal force may be obtained from the horizontal component weight of the train B. to avoid frictional force between the tracks and wheels C. necessary centripetal force may be obtained from the horizontal component of the weight of the train D. the train may not fly off in the opposite direction

Answer - Option C
12. Who was the first president of Uzbekistan?

A. Abdulhashim Mutalov B. Oʻtkir Sultonov C. Islam Karimov D. Nigmatilla Yuldashev

Answer - Option C
13. Which of the following eminent personalities who was the ninth monarch of Thailand from the Chakri Dynasty as Rama IX?

A. Sirikit Kitiyakara B. Vajiralongkorn C. Ananda Mahidol D. Bhumibol Adulyadej

Answer - Option D
14. In what year was Rajiv Gandhi assassinated?

A. 1990 B. 1991 C. 1992 D. 1993

Answer - Option B
15. Who was the 1st Prime Minister of India?

A.Pandit Jawaharlal Nehru B. Lal Bahadur Shastri C. Gulzar Lal Nanda D. None of the Above

Answer - Option
Explanation -
16. Who was the founder of the Theosophical Society in India and started the Home Rule League?

A. Annie Besant B. Acharya Narendra Dev C. Lal-Bal-Pal D. None of the above

Answer - Option A
17. What is the annual premium payable by the subscriber to the Pradhan Mantri Jeevan Jyoti Bima Yojana?

A. Rs. 210 B. Rs. 330 C. Rs. 450 D. Rs. 510

Answer - Option B
18. What is the minimum age at which a subscriber can join the Atal Pension Yojana?

A. 25 years B. 22 years C. 18 years D. 15 years

Answer - Option C
19. What is the overdraft allowed to the account holder after 6 months of satisfactory operation of Pradhan Mantri Jan Dhan Yojana account?

A. Rs. 3000 B. Rs. 5000 C. Rs. 7000 D. Rs. 10000

Answer - Option B
20. What is the slogan of the Pradhan Mantri Jan Dhan Yojana?

A. Sabka Saath Sabka Vikas B. Beti Bachao Beti Padhao C. Kal ki Fikr Nahin D. Mera Khata Bhagya Vidhata

Answer - Option D
21. What is the maximum number of accounts a natural or legal guardian can open for his girl children under the Sukanya Samriddhi Yojana?

A. One B. Two C. Three D. Equal to the number of girl children

Answer - Option C
22. What is the annual premium payable under the Pradhan Mantri Suraksha Bima Yojana?

A. Rs. 12 B. Rs. 15 C. Rs. 18 D. Rs. 20

Answer - Option A
23. When was the government of India had launched the Project Snow Leopard?

A. 2000 B. 2003 C. 2009 D. 2012

Answer - Option C
24. When was the Project Tiger launched?

A. 1973 B. 1975 C. 1974 D. 1976

Answer - Option A
25. Which of the following Mike Sites is not correctly matched?

A. Deomali - Arunachal Pradesh B. Garo Hills - Meghalaya C. Mayurbhanj - Chhattisgarh D. Mysore - Karnataka

Answer - Option C
26. Which of the following is not a type of computer on the basis of operation?

A. Remote B. Hybrid C. Analog D. Digital

Answer - Option A
Explanation - There are three types of computers basically on the basis of operation: Analog, Digital and Hybrid.
27. They can operate on batteries and hence are very popular with travelers.

A. Mainframes B. Laptops C. Microprocessors D. Hybrid

Answer - Option B
Explanation - Laptops can operate on batteries and hence are very popular with travelers. The screen folds down onto the keyboard when not in use.
28. PDA stands for?

A. personal digital applications B. private digital applications C. personal digital assistants D. private digital assistants

Answer - Option B
Explanation -PDA stands for Personal Digital Assistants. They are pen-based and also battery powered.
29. Each box in a spreadsheet is called is called a......

A. cell B. empty space C. record D. field

Answer - Option A
30. You can use.....to copy selected text; and .....to paste it in a document.

A. CTRL+C, CTRL+V B. CTRL+C, CTRL+P C. CTRL+S, CTRL+S D. SHIFT+C, ALT+P

Answer - Option A
31. Who had given the slogan of 'Do or Die'during All India Congress Committee in Bombay and ratified the 'Quit India' resolution?

A. Mahatma Gandhi B. Jawaharlal Nehru C. Subhash Chandra Bose D. Jayaprakash Narayan

Answer - Option A
32. When was the 'Quit India Movement' Launched by Mohandas Karamchand Gandhi?

A. 1946 B. 1939 C. 1942 D. 1940

Answer - Option C
33. Which of the following leader who presided All India Congress Committee session on 9th August?

A. Jawaharlal Nehru B. Aruna Asif Ali C. Mahatma Gandhi D. Annie Besant

Answer - Option B
34. What was the another name of 'Pledge of Indian Independence'?

A. Declaration of Independence B. Declaration of Constitution C. Declaration of Constituent Assembly D. None of the above<

Answer - Option A
35. Who among the following wrote the Kural, which deals with many aspects of life and religion?

A. Thiruvalluvar B. Ayaikar C. Shankracharya D. Rishi Agasta

Answer - Option A
36. Which is a work of Tamil Grammar that is said to be the earliest extant work of Tamil Literature?

A. Tolkāppiyam B. Patinenmēlkanakku C. Patinenkīlkanakku D. None of the above

Answer - Option A
37. Which Sangam literature was composed by Jain monks and the theme is the transient nature of life and youth?

A. Nanmanikkatiga B. Naaladiyar C. Inna Narpathu D. Iniyavai Narpathu

Answer - Option B
38. Which statement (s) is/are correct about Aryankas? I. It is a treatise of forest which explain the the rituals while dwelling into the philosophical discussions of the Brahmanas. II. They record the transitions between ritualistic symbolism of Brahmanas and philosophical aspects of Upanishads.

A. Only I B. Only II C. Both I & II D. Neither I nor II

Answer - Option C
39. Brass gets discoloured in air because of the presence of which of the following gases in air?

A. Oxygen B. Hydrogen sulphide C. Carbon dioxide D. Nitrogen

Answer - Option B
40. Which Ancient Indian literature deals with concepts about origin of universe, death and birth, material and spiritual world?

A. Rig Vedas B. AtharvaVedas C. Aryankas D. Upanishad

Answer - Option D
41.Which of the following is used in pencils?

A. Graphite B. Silicon C. Charcoal D. Phosphorous

Answer - Option A
42. The gases used in different types of welding would include

A. oxygen and hydrogen B. oxygen, hydrogen, acetylene and nitrogen C. oxygen, acetylene and argon D. oxygen and acetylene

Answer - Option D
43. The property of a substance to absorb moisture from the air on exposure is called

A. osmosis B. deliquescence C. efflorescence D. desiccation

Answer - Option B
44. The Homolographic projection has the correct representation of

A. shape B. area C. baring D. distance

Answer - Option B
45. The latitudinal differences in pressure delineate a number of major pressure zones, which correspond with

A. zones of climate B. zones of oceans C. zones of land D. zones of cyclonic depressions<

Answer - Option A
46. Which of the following is not associated with the UNO?

A. ILO B. WHO C. ASEAN D. All of the above

Answer - Option C
47. The chairmanship/presidency of the UN Security Council rotates among the Council Members

A. every 6 months B. every 3 months C. every year D. every month

Answer - Option D
Explanation -
48. The Indian delegation to the first World Conference on Human Rights was led by

A. Dr. Manmohan Singh B. Farooq Abdullah C. Dinesh singh D. Alam Khan

Answer - Option A
49. Which of the following is not the management category of roads in India?

A. National Highways B. State Highways C. Border Roads D. District Highways

Answer - Option D
50. When Indian Railways was nationalised?

A. 1948 B. 1949 C. 1950 D. 1951

Answer - Option C

1.Simplify the expression using BODMAS rule:: ([latex]\frac {3}{2}[/latex]) of ([latex]\frac {4}{7}[/latex]) {(10 × 3) – (8 × 2)}

A. 6 B. 12 C. 18 D. 14

Answer - Option B
Explanation - Applying BODMAS rule = ([latex]\frac {3}{2}[/latex]) of ([latex]\frac {4}{7}[/latex]) {30 – 16} = ([latex]\frac {12}{14}[/latex]) × 14 = 12 Therefore, the correct answer is option 2.
2. The six digit number 54321A is divisible by 9 where A is a single digit whole number. Find A.

A. 0 B. 2 C. 4 D. 3

Answer - Option D
Explanation -A number is divisible by 9, when the sum of its digits is divisible by 9. Here, 5 + 4 + 3 + 2 + 1 + A = 15 + A should be divisible by 9. Therefore, A = 3 gives 15+ 3 = 18 as the sum of digits, which is divisible by 9. So, answer is option 4.
3. Find the fractional equivalent of 6789.

A. [latex]\frac {5111}{9000}[/latex] B. [latex]\frac {6117}{9000}[/latex] C. [latex]\frac {6119}{9000}[/latex] D. None of these

Answer - Option D
Explanation - 6789 = [latex]\frac {(6789-678)}{9000}[/latex] = [latex]\frac {6111}{9000}[/latex]
4. In a library 2/3 of books are in English and the remaining 300 are of Hindi. Find the total books in library

A. 400 B. 900 C. 275 D. None of these

Answer - Option B
Explanation -[latex]\frac {2}{3}[/latex] of books are in English means remaining 1 – [latex]\frac {2}{3}[/latex] = [latex]\frac {1}{3}[/latex] are in Hindi which is equal to 300. So 1/3rd of total = 300 ⇒ Total books = 300 x 3 = 900.
5. Which of the following fraction is the largest?

A. [latex]\frac {8}{9}[/latex] B. [latex]\frac {18}{23}[/latex] C. [latex]\frac {13}{21}[/latex] D. [latex]\frac {14}{17}[/latex]

Answer - Option A
Explanation -Converting the given fractions into decimal form, we have, [latex]\frac {8}{9}[/latex] = 0.88 [latex]\frac {18}{23}[/latex] = 0.78 [latex]\frac {13}{21}[/latex] = 0.76 [latex]\frac {14}{17}[/latex] = 0.82 From the above, 0.88 is the largest. The corresponding fraction is. = [latex]\frac {8}{9}[/latex]
6. Bala and Aruna can complete a work in 30 days. Bala can do it alone in 50 days. How many days would Aruna take to complete the work alone?

A. 100 days B. 100 days C. 90 days D. 75 days

Answer - Option D
Explanation -By using the alternate method as mentioned in Question 1, we are going to solve further problems. LCM of 30 and 50 is 150. Bala and Aruna can complete the whole work in 30 days. In 1 day they can complete 5(150/30) of the work. Bala alone can complete the whole work in 50 days. In 1 day he can complete 3(150/30) of the work. Aruna alone can complete in 1 day (5 - 3)of the work. Therefore, Aruna will complete the whole work in [latex]\frac {150}{2}[/latex] = 75 days.
7. Prakash can complete a piece of work in 24 days and Praveen can complete the same piece of work in 36 days. If Prakash and Praveen work together, how long would they take to complete the work?

A. 14.4 days B. 15.5 days C. 12 days D. 20 days

Answer - Option A
Explanation - Prakash can complete in one day = [latex]\frac {1}{24}[/latex] of work. Praveen can complete in one day = [latex]\frac {1}{36}[/latex] of work. Prakash and Praveen can complete in one day = [latex]\frac {1}{24}[/latex] + [latex]\frac {1}{36}[/latex] of work. = 3 + [latex]\frac {2}{72}[/latex] = [latex]\frac {5}{72}[/latex] Both can complete the work in 72/5 days. i.e., 14.4 days Usually, we will solve this type of problem in the above method. There is another alternative method to solve these types of problems. i.e., we can solve by using the LCM method instead of the fraction method.
8. if the numerator and denominator of a fraction is diminished and increased by 70% respectively then the resultant fraction is [latex]\frac {39}{34}[/latex] . find the original fraction.

A. [latex]\frac {17}{11}[/latex] B. [latex]\frac {13}{11}[/latex] C. [latex]\frac {13}{2}[/latex] D. [latex]\frac {17}{2}[/latex]

Answer - Option C
Explanation - let the original fraction be [latex]\frac {X}{Y}[/latex] then (30% of x)/(170% of y) = [latex]\frac {39}{34}[/latex] x/y = ([latex]\frac {39}{34}[/latex])*([latex]\frac {170}{30}[/latex]) = [latex]\frac {13}{2}[/latex]
9. The percentage of numbers from 11 to 75 which are divided by 5 or 7 is:

A. 31 B. 35 C. 36 D. 41

Answer - Option A
Explanation - Clearly, the numbers which divided by 5 or 7 from 11 to 75 are 14, 15, 20, 21, 25, 28, 30, 35, 40, 42, 45, 49, 50, 55, 56, 60, 63, 65, 70, 75. The number of such numbers = 20 Total numbers from 11 to 75 = 65 Then the required percentage = (20/65) x 100 = 30.76% = 31 % Hence the answer is 31%
10. Ramu buys 3 dozen tomatoes for Rs. 360. He buys carry bags to take them to his shop. Only one dozen can be filled into a carry bag and cost of each carry bag is Rs.10. He then sells the tomatoes along with carry bags for a cost of 200 per dozen. What is his profit percentage.

A. 53.84% B. 60% C. 56.67% D. 63.84%

Answer - Option A
Explanation - Cost of 3 dozens of tomatoes is Rs. 360 Cost of 1 carry bag = Rs. 10. Therefore, three of them cost Rs. 30 Overall CP of tomatoes = 360 + 30 = Rs. 390 SP of each dozen of tomatoes = Rs. 200 Therefore SP of three dozens = 600 Profit percentage = (SP - CP) / CP x 100% = (600 - 390)/390 x 100% = 210/390x 100% = 2100/39 % = 53.84%
11. Ravi buys a second hand car for Rs. 2,00,000. He then repaints it for Rs. 2000. He attaches new threading to all 4 tyres. Cost of threading per tyre is Rs. 200. At what price he should resell the car so that he gains 10%.

A. Rs. 223080 B. Rs. 223090 C. Rs. 232080 D. Rs. 223880

Answer - Option A
Explanation - Cost of second hand car = Rs. 2,00,000 Repainting cost = Rs. 2000 Cost of threading per tyre = Rs. 200 Cost of threading for all tyres = Rs. 200 x 4 = Rs. 800 Total costs involved = Actual cost + Repainting costs + Threading costs = 2,00,000 + 2000 + 800 = 202800 Profit Percentage = 10% = (SP - CP)/CP x 100% Or 10% = (SP - 202800)/202800 x 100% Or 10 = (SP - 202800)/2028 Or SP = 20280 + 202800 = 223080
12. A bike at a speed of 60km/hr, it covers certain distance in 3 hours and the train can cover the same distance in 1 and half hours then the speed of train is

A. 80km/hr B. 120km/hr C. 160km/hr D. 50km/hr

Answer - Option B
Explanation - The diatance covered by the bike with speed 60km/hr in 3 hours = (60 x 3) = 180 km Now, Speed = Distance/Time since the train covers the same 180 km in 3/2 hours (we can write 1 and half hours as 3/2 hours) Then the speed of the train = 180/ (3/2) = 120 km/hr. Hence the train traveled at the speed of 120km/hr to cross 180km in 1 and half hours.
13. A car starts at A and reaches a destination in 8 hours. If it travels first and second half at the speed of 80 km/hr and 100 km/hr respectively then the distance between A and destination is:

A. 818km B. 979km C. 711km D. 850km

Answer - Option C
Explanation - Let the distance between A and destination be X. The total time taken by the car to cover X = 8 hours Since X/2 by 80km/hr and remaining X/2 by 100km/hr Then by Time = distance/speed, we have (X/2)/80 + (X/2)/100 = 8 X/80 + X/100 = 16 5X + 4X = 6400 9X = 6400 X = 6400/9 = 711 Hence 711km is the required answer.
14. If A and B are connected by the relation [latex]{A}^{2}[/latex] + 4[latex]{B}^{2}[/latex] = 4AB then A:B is:

A. 2:1 B. 1:2 C. 3:1 D. 2:1

Answer - Option A
Explanation - Given that the relation of A and B is [latex] {A}^{2}[/latex] + 4[latex]{B}^{2}[/latex] = 4AB [latex]{A}^{2}[/latex] + 4[latex]{B}^{2}[/latex]- 4AB = 0 [latex]{(A - 2B)}^{2}[/latex] = 0 (by [latex]{(X - Y)}^{2}[/latex] = [latex]{X}^{2}[/latex] + [latex]{Y}^{2}[/latex] - 2xy ) (A - 2B) = 0 A = 2B [latex]\frac {A}{B}[/latex] = [latex]\frac {2}{1}[/latex] Hence, the answer is A:B = 2:1
15. An amount of money was lent for 3 years. What will be the difference between the simple and the compound interest earned on it at the same rate? I. The rate of interest was 8 p.c.p.a. II. The total amount of simple interest was Rs. 1200.

A. I alone sufficient while II alone not sufficient to answer B. II alone sufficient while I alone not sufficient to answer C. Either I or II alone sufficient to answer D. Both I and II are necessary to answer

Answer - Option D
Explanation - Given: T = 3 years. I. gives: R = 8% p.a. II. gives: S.I. = Rs. 1200. Thus, P = Rs. 5000, R = 8% p.a. and T = 3 years. Difference between C.I. and S.I. may be obtained. So, the correct answer is (E).
16. What will be the least number which when doubled will be exactly divisible by 12,18,21 and 30?

A. 630 B. 360 C. 603 D. 306

Answer - Option A
Explanation - LCM of 12,18,21 and 30 = 1260 Doubled (divide by 2) = [latex]\frac {1260}{2}[/latex] = 630
17. HCF and LCM of two numbers are 11 and 385 .If one number lies between 75 and 125 then that number is

A. 123 B. 73 C. 77 D. 154

Answer - Option C
Explanation - Product of the two number = 11a×11b = 4235 11a×11ab = [latex]\frac {4235}{12}[/latex] = 35 35 = 7 × 5 (co prime) 77 × 11 = 77
18. The HCF of 2511 and 3402 is

A. 31 B. 81 C. 45 D. 21

Answer - Option B
Explanation - 2511 = 81×31 3402 = 81×42 Hence HCF is 81
19. In a rectangle the ratio of the length and breadth is 3:2. If each of the length and breadth is increased by 4m their ratio becomes 10:7. The area of the original rectangle in m² is?

A. 846 B. 864 C. 840 D. 876

Answer - Option B
Explanation - [latex]\frac {3x + 4}{2x + 4}[/latex] = [latex]\frac {10}{7}[/latex] x = 12 Area of the original rectangle = 3x x 2x = 6x² Area of the original rectangle = 6 x 144 = 864m²
20. The area of a rectangle gets reduced by 9 square units,if its length is reduced by 5 units and breadth is increased by 3 units. If we increase the length by 3 units and breadth by 2 units, then the area is increased by 67 square units. Find the area of the rectangle?

A. 159m B. 179m C. 147m D. 153m

Answer - Option D
Explanation - Length = x; Breadth =y xy – (x-5)(y+3) = 9 3x – 5y – 6 = 0 —(i) (x + 3)(y + 2) – xy = 67 2x + 3y - 61 = 0 —(ii) solving (i) and (ii) x = 17m ; y = 9m Area of the Rectangle = 153 m
21. The width of a rectangular piece of land is 1/4 th of its length. If the perimeter of the piece of land is 320m its length is?

A. 140M B. 128M C. 120M D. 156M

Answer - Option B
Explanation - length = l ; breadth = [latex]\frac {1}{4}[/latex] 2(l + b) = 320 2(l + [latex]\frac {1}{4}[/latex]) = 320 l = 320 x [latex]\frac {4}{10}[/latex] = 128m
22. The perimeter of a rectangle and a square is 160 cm each. If the difference between their areas is 500 cm. If the area of the rectangle is less than that of a Square then find the area of the rectangle?

A. 1800 cm² B. 1500 cm² C. 1100 cm² D. 1600 cm²

Answer - Option C
Explanation - Perimeter of rectangle = Perimeter of Square = 160 4a = 160 => a = 40 Area of square = 1600 1600 – lb = 500 lb = 1100 cm²
23. Tickets numbered 1 to 20 are mixed up and then a ticket is drawn at random. What is the probability that the ticket drawn has a number which is a multiple of 3 or 5?

A. [latex]\frac {1}{2}[/latex] B. [latex]\frac {2}{5}[/latex] C. [latex]\frac {8}{15}[/latex] D. [latex]\frac {9}{20}[/latex]

Answer - Option D
Explanation - Here, S = {1, 2, 3, 4, ...., 19, 20}. Let E = event of getting a multiple of 3 or 5 = {3, 6 , 9, 12, 15, 18, 5, 10, 20}. P(E) =[latex]\frac {n(E)}{n(S)}[/latex] =[latex]\frac {9}{20}[/latex]
24. Two dice are thrown simultaneously. What is the probability of getting two numbers whose product is even?

A. [latex]\frac {1}{2}[/latex] B. [latex]\frac {3}{4}[/latex] C. [latex]\frac {3}{8}[/latex] D. [latex]\frac {5}{16}[/latex]

Answer - Option B
Explanation - In a simultaneous throw of two dice, we have n(S) = (6 x 6) = 36. Then, E = {(1, 2), (1, 4), (1, 6), (2, 1), (2, 2), (2, 3), (2, 4), (2, 5), (2, 6), (3, 2), (3, 4), (3, 6), (4, 1), (4, 2), (4, 3), (4, 4), (4, 5), (4, 6), (5, 2), (5, 4), (5, 6), (6, 1), (6, 2), (6, 3), (6, 4), (6, 5), (6, 6)} => n(E) = 27. P(E) = [latex]\frac {n(E)}{n(S)}[/latex][latex]\frac {27}{36}[/latex][latex]\frac {3}{4}[/latex]
25. In a lottery, there are 10 prizes and 25 blanks. A lottery is drawn at random. What is the probability of getting a prize?

A. [latex]\frac {1}{10}[/latex] B. [latex]\frac {2}{5}[/latex] C. [latex]\frac {2}{7}[/latex] D. [latex]\frac {5}{7}[/latex]

Answer - Option C
Explanation - P (getting a prize) = [latex]\frac {10}{10+25}[/latex]=[latex]\frac {10}{35}[/latex]=[latex]\frac {2}{7}[/latex]
26. One card is drawn at random from a pack of 52 cards. What is the probability that the card drawn is a face card (Jack, Queen and King only)?

A. [latex]\frac {1}{13}[/latex] B. [latex]\frac {3}{13}[/latex] C. [latex]\frac {1}{4}[/latex] D. [latex]\frac {9}{52}[/latex]

Answer - Option B
Explanation - Clearly, there are 52 cards, out of which there are 12 face cards. P (getting a face card) = [latex]\frac {12}{52}[/latex]=[latex]\frac {3}{13}[/latex]
27. The value of sin (45° + θ) – cos (45° – θ) is

A. 1 B. 0 C. 2 cos θ D. 2 sin θ

Answer - Option B
Explanation - sin(45° + θ) – cos(45° – θ) = sin{90° – (45° – θ)} – cos (45° – θ) = cos (45° – θ) – cos (45° – θ) {∵sin(90 – A) = cos A } = 0
28. If sin (A + B) = 1, where 0 < B < 45°, then what is cos (A – B) equal to?

A. sin 2B B. sin B C. cos 2B D. cos B

Answer - Option A
Explanation - ∵ sin (A + B) = 1 ⇒ A + B = [latex]{sin}^{-1}[/latex] 1 ⇒ (A + B) = 90° ⇒ B = 90° – A ⇒ A = 90° – B Now, cos (A – B) = cos A cos B + sin A + sin B = cos (90 – B) cos B + sin (90 – B) sin B = sin B cos B + cos B sin B = 2 sin B cos B = sin 2B.
29. What is sin 25° sin 35° sec 65° sec 55° equal to?

A. 1 B. -1 C. -2 D. 0

Answer - Option A
Explanation - sin 25° sin 35° sec 65° sec 55° = sin25°.sin35°[latex]\frac {1}{cos65°}[/latex][latex]\frac {1}{cos55°}[/latex] = sin25°.sin35°[latex]\frac {1}{sin25°}[/latex][latex]\frac {1}{sin35°}[/latex] [ ∵ cos(90 – Θ) = sinΘ ] = 1.
30. Three candidates contested an election and received 1136, 7636 and 11628 votes respectively. What percentage of the total votes did the winning candidate get?

A. 57% B. 60% C. 65% D. 90%

Answer - Option A
Explanation - Total number of votes polled = (1136 + 7636 + 11628) = 20400. Required percentage = [latex]\frac {11628}{20400}[/latex] x 100% = 57%.
31. A sum of money at simple interest amounts to Rs. 815 in 3 years and to Rs. 854 in 4 years. The sum is:

A. Rs. 650 B. Rs. 690 C. Rs. 698 D. Rs. 700

Answer - Option C
Explanation - S.I. for 1 year = Rs. (854 - 815) = Rs. 39. S.I. for 3 years = Rs.(39 x 3) = Rs. 117. Principal = Rs. (815 - 117) = Rs. 698.
32. A sum fetched a total simple interest of Rs. 4016.25 at the rate of 9 p.c.p.a. in 5 years. What is the sum?

A. Rs. 4462.50 B. Rs. 8032.50 C. Rs. 8900 D. Rs. 8925

Answer - Option D
Explanation - Principal = Rs [latex]\frac {100 x 4016.25 }{9 x 5}[/latex] = Rs [latex]\frac {401625}{45}[/latex] = Rs. 8925.
33. Reena took a loan of Rs. 1200 with simple interest for as many years as the rate of interest. If she paid Rs. 432 as interest at the end of the loan period, what was the rate of interest?

A. 3.6 B. 6 C. 18 D. Cannot be determined

Answer - Option B
Explanation - Let rate = R% and time = R years. Then,[latex]\frac {1200 x R x R }{100}[/latex]= 432 => 12[latex]{R}^{2}[/latex] = 432 =[latex]{R}^{2}[/latex]= 36 =R = 6.
34. Let N be the greatest number that will divide 1305, 4665 and 6905, leaving the same remainder in each case. Then sum of the digits in N is:

A. 3 B. 4 C. 6 D. 5

Answer - Option B
Explanation - N = H.C.F. of (4665 - 1305), (6905 - 4665) and (6905 - 1305) = H.C.F. of 3360, 2240 and 5600 = 1120. Sum of digits in N = ( 1 + 1 + 2 + 0 ) = 4
35. The greatest number of four digits which is divisible by 15, 25, 40 and 75 is:

A. 9600 B. 9800 C. 9500 D.
Answer - Option A
Explanation - Greatest number of 4-digits is 9999. L.C.M. of 15, 25, 40 and 75 is 600. On dividing 9999 by 600, the remainder is 399. Required number (9999 - 399) = 9600.

1. Odometer is to mileage as compass is to

A. speed B. hiking C. needle D. direction

Answer - Option D
Explanation - An odometer is an instrument used to measure mileage. A compass is an instrument used to determine direction. Choices a, b, and c are incorrect because none is an instrument.
2. Marathon is to race as hibernation is to

A. winter B. bear C. dream D. sleep

Answer - Option D
Explanation - A marathon is a long race and hibernation is a lengthy period of sleep. The answer is not choice a or b because even though a bear and winter are related to hibernation, neither completes the analogy. (Choice c) is incorrect because sleep and dream are not synonymous.
3. EXPLORE : DISCOVER

A. read : skim B. research : learn C. write : print D. hink : relate

Answer - Option B
Explanation - One explores to discover; one researches to learn.
4. 120, 99, 80, 63, 48, ?

A. 35 B. 38 C. 39 D. 40

Answer - Option A
Explanation - The pattern is - 21, - 19, - 17, - 15,..... So, missing term = 48 - 13 = 35.
5. 121, 143, 165, 186, 209

A. 143 B. 165 C. 186 D. 209

Answer - Option C
Explanation - Each term in the series is obtained by adding 22 to the preceding term. So, 186 is wrong and must be replaced by (165 + 22) i.e. 187.
6. Statements: All the harmoniums are instruments. All the instruments are flutes. Conclusions: 1. All the flutes are instruments. 2. All the harmoniums are flutes.

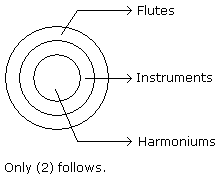
A. Only (1) conclusion follows B. Only (2) conclusion follows C. Either (1) or (2) follows D. Neither (1) nor (2) follows

Answer - Option B
Explanation -
7. Statements: Some mangoes are yellow. Some tixo are mangoes. Conclusions: 1. Some mangoes are green. 2. Tixo is a yellow.

A. Only (1) conclusion follows B. Only (1) conclusion follows C. Either (1) or (2) follows D. Neither (1) nor (2) follows

Answer - Option D
Explanation -
8. b e d f ? h j ? l

A. i m B. m i C. i n D. j m

Answer - Option A
Explanation - The series may be divided into groups as shown: b e d / f ? h / j ? l Clearly in the first group, the second and third letters are respectively three and two steps ahead of the first letter. A similar pattern would follow in the second and third groups.
9. gfe _ ig _ eii _ fei _ gf_ ii

A. eifgi B. figie C. ifgie D. ifige

Answer - Option C
Explanation - The series is gfeii/gfeii/gfeii/gfeii. Thus, the pattern 'gfeii' is repeated.
10. In a certain code 'ROAR' is written as 'URDU'. How is 'URDU' written in that code

A. V X D Q B. XUGX C. ROAR D. VSOV

Answer - Option B
Explanation - Each letter moves +3. Add 3 to each letter of URDU,so code of URDU will be XUGX
11. If in the English alphabet, every alternate letter from B onwards is written in small letters while others are written in capitals, then how will the 3rd day from Tuesday will be coded?

A. W e D N e S d A Y B. W E d n E S d A Y C. T H U R S d A Y D. f r I d A Y

Answer - Option D
Explanation - The small letters are b, d, f, h, j, l, n, p, r, t, v, x, z. The third day from tuesday will be friday and code will be frIdAY.
12. If ‘+’ means ‘÷’, ‘–‘ means ‘×’, ‘×’ means ‘+‘, ‘÷’ means ‘– ‘, given the value of 45 + 9 – 3 × 15 ÷ 2.

A. 40 B. 28 C. 65 D. 58

Answer - Option B
Explanation - → 45 ÷ 9 × 3 + 15 – 2. = 5 × 3 + 15 – 2. = 15 + 15 – 2 = 28.
13. If ‘R’ stands for ‘–‘, ‘A’ stands for ‘+’, ‘B’ stands for ‘÷’ and ‘C’ stands for ‘×’, then what is the value of the given equation ? 25 A 37 C 2 B 4 R 1 = ?

A. 52 B. 25 C. 30 D. 24

Answer - Option C
Explanation - According to the question, after putting signs = 25 + 37 × 2 ÷ 4 – 1 = 62 × 2 ÷ 4 – 1 = 124 ÷ 4 – 1 = 31 – 1 = 30.
14. Pointing to a photograph of a boy Suresh said, "He is the son of the only son of my mother." How is Suresh related to that boy?

A. Brother B. Uncle C. Cousin D. Father

Answer - Option D
Explanation - The boy in the photograph is the only son of the son of Suresh's mother i.e., the son of Suresh. Hence, Suresh is the father of boy.
15. If A is the brother of B; B is the sister of C; and C is the father of D, how D is related to A?

A. Brother B. Sister C. Nephew D. Cannot be determined

Answer - Option D
Explanation - If D is Male, the answer is Nephew. If D is Female, the answer is Niece. As the sex of D is not known, hence, the relation between D and A cannot be determined. Note: Niece - A daughter of one's brother or sister, or of one's brother-in-law or sister-in-law. Nephew - A son of one's brother or sister, or of one's brother-in-law or sister-in-law.
16. If A + B means A is the brother of B; A - B means A is the sister of B and A x B means A is the father of B. Which of the following means that C is the son of M?

A. M - N x C + F B. F - C + N x M C. N + M - F x C D. M x N - C + F

Answer - Option D
Explanation - M x N → M is the father of N N - C → N is the sister of C and C + F → C is the brother of F. Hence, M is the father of C or C is the son of M.
17. Find the number of triangles in the given figure.

A. 12 B. 18 C. 11 D. 10

Answer - Option B
Explanation - The figure may be labelled as shown. The simplest triangles are AHB, GHI, BJC, GFE, GIE, IJE, CEJ and CDE i.e. 8 in number. The triangles composed of two components each are HEG, BEC, HBE, JGE and ICE i.e. 5 in number. The triangles composed of three components each are FHE, GCE and BED i.e. 3 in number. There is only one triangle i.e. AGC composed of four components. There is only one triangle i.e. AFD composed of nine components. Thus, there are 8 + 5 + 3 + 1 + 1 = 18 triangles in the given figure.
5 persons A, B, C, D and E are having a different number of marbles with them. The number of marbles with them are 7,8,9,4 and 6 not necessarily in the same order. The number of marbles with A and B is one more than the number of marbles with E. C has more marbles than D. A has more marbles than B.
18. Who has 8 marbles?...

A. C B. v D C. A D. B

Answer - Option A
Explanation - The number of marbles with A and B is one more than the number of marbles with E. Therefore, A and B must have 6 and 4 marbles (in any order) and E must have 9 marbles. A has more marbles than B. There fore, A must have 6 marbles and B must have 4 marbles. C has more marbles than D. Since we know that E has 9 marbles, C must be having 8 marbles and D must be having 7 marbles. The number of persons with each of the persons is as follows:... 4 -B, 6 -A, 7 -D, 8 -C, 9 -E C has 8 marbles. Therefore, option A is the right answer....
19. Eileen is planning a special birthday dinner for her husband's 35th birthday. She wants the evening to be memorable, but her husband is a simple man who would rather be in jeans at a baseball game than in a suit at a fancy restaurant. Which restaurant below should Eileen choose?

A. Alfredo's offers fine Italian cuisine and an elegant Tuscan decor. Patrons will feel as though they've spent the evening in a luxurious Italian villa. B. Pancho's Mexican Buffet is an all-you-can-eat family style smorgasbord with the best tacos in town. C. The Parisian Bistro is a four-star French restaurant where guests are treated like royalty. Chef Dilbert Olay is famous for his beef bourguignon. D. Marty's serves delicious, hearty meals in a charming setting reminiscent of a baseball clubhouse in honor of the owner,Marty Lester, a former major league baseball all-star.

Answer - Option D
Explanation - Since Eileen's husband does not enjoy fancy restaurants, choices a and c can be ruled out. Choice b, although casual, doesn't sound as though it would be the kind of special and memorable evening that Eileen is looking for. Choice d, which is owned by a former baseball star and is described as "charming" and "reminiscent of a baseball clubhouse", sounds perfect for Eileen's husband, who is described as a baseball fan and a man with simple tastes.
20. The school principal has received complaints from parents about bullying in the school yard during recess. He wants to investigate and end this situation as soon as possible, so he has asked the recess aides to watch closely. Which situation should the recess aides report to the principal?

A. A girl is sitting glumly on a bench reading a book and not interacting with her peers. B. Four girls are surrounding another girl and seem to have possession of her backpack. C. Four girls are surrounding another girl and seem to have possession of her backpack. D. Three boys are huddled over a handheld video game, which isn't supposed to be on school grounds.

Answer - Option B
Explanation -Seeing four girls surrounding another girl, while in possession of her backpack, is the most suspicious of the incidents described.
Directions(21 - 25):The bar graph given below shows the foreign exchange reserves of a country (in million US $) from 1991 - 1992 to 1998 - 1999.
21. The ratio of the number of years, in which the foreign exchange reserves are above the average reserves, to those in which the reserves are below the average reserves is?

A. 2:8 B. 3:5 C. 2:5 D. 3:7

Answer - Option B
Explanation - Average foreign exchange reserves over the given period = 3480 million US $. The country had reserves above 3480 million US $ during the years 1992-93, 1996-97 and 1997-98, i.e., for 3 years and below 3480 million US $ during the years 1991-92, 1993-94, 1994-95, 1995-56 and 1998-99 i.e., for 5 years. Hence, required ratio = 3 : 5.
22. The foreign exchange reserves in 1997-98 was how many times that in 1994-95?

A. 1:5 B. 0:5 C. 2:54 D. 0:2

Answer - Option A
Explanation -Required ratio =[latex]\frac {5040}{3360}[/latex]= 1.5.
23. For which year, the percent increase of foreign exchange reserves over the previous year, is the highest?

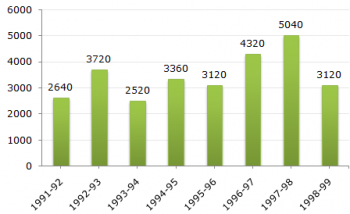
A. 1992-93 B. 1993-94 C. 1994-95 D. 1996-97

Answer - Option A
Explanation -There is an increase in foreign exchange reserves during the years 1992 - 1993, 1994 - 1995, 1996 - 1997, 1997 - 1998 as compared to previous year (as shown by bar-graph). The percentage increase in reserves during these years compared to previous year are: For 1992 - 1993 = [latex]\frac {(3720 - 2640)}{2640}[/latex] X 100% = 40.91%. For 1994 - 1995 = [latex]\frac {(3360 - 2520)}{2520}[/latex]X 100% = 33.33% For 1996 - 1997 = [latex]\frac {(4320 - 3120)}{3120}[/latex]X 100% =38.46% For 1997 - 1998 = [latex]\frac {(5040 - 4320)}{4320}[/latex]X 100% =16.67% Clearly, the percentage increase over previous year is highest for 1992 - 1993.
24. The foreign exchange reserves in 1996-97 were approximately what percent of the average foreign exchange reserves over the period under review?

A. 95% B. 110% C. 115% D. 125%

Answer - Option D
Explanation - Average foreign exchange reserves over the given period = [latex]\frac {1}{8}[/latex]x (2640 + 3720 + 2520 + 3360 + 3120 + 4320 + 5040 + 3120) = 3480 million US $. Foreign exchange reserves in 1996 - 1997 = 4320 million US $. Required percentage = [latex]\frac {4320}{3480}[/latex] X 100% = 124.14% ~= 125%
25. What was the percentage increase in the foreign exchange reserves in 1997-98 over 1993-94

A. 100 B. 150 C. 200 D. 250

Answer - Option
Explanation - Foreign exchange reserves in 1997 - 1998 = 5040 million US $. Foreign exchange reserves in 1993 - 1994 = 2520 million US $. Therefore Increase = (5040 - 2520) = 2520 US $. Percentage Increase = [latex]\frac {2520}{2520}[/latex] X 100% = 100%
26. A man walks 5 km toward south and then turns to the right. After walking 3 km he turns to the left and walks 5 km. Now in which direction is he from the starting place?

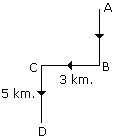
A. West B. South C. North-East D. South-West

Answer - Option D
Explanation - Hence required direction is South-West.
27. One morning after sunrise, Vimal started to walk. During this walking he met Stephen who was coming from opposite direction. Vimal watch that the shadow of Stephen to the right of him (Vimal). To Which direction Vimal was facing?

A. East B. West C. South D. Data inadequate

Answer - Option C
Explanation - Sun rises in the east. So the shadow of a man will always falls towards the west. Since the shadow of Stephen is to the right of Vimal. Hence Vimal is facing towards South
28. Lali and Anju are a married couple. Tunu and Munu are brothers. Tunu is the brother of Lali. How is Munu related to Anju?

A. Brother B. Brother-in-law C. Sister-in-law D. None of these

Answer - Option B
Explanation - Since Tunu and Munu are brothers, and Tunu is the brother of Lali, Munu is also the brother of Lali. Thus, Munu is the brother-in-law of Anju.
29. Pointing towards a lady, Neeraj said. “ She is the daughter of the only child of my grandmother.” How is the lady related to Neeraj ?

A. Sister B. Niece C. Cousin D. None of these

Answer - Option A
Explanation - The only child of Neeraj's grandmother is Neeraj's father. Now daughter of Neeraj's father is Neeraj's sister.
30. Statement: Severe drought is reported to have set in several parts of the country. Courses of Action: 1. Government should immediately make arrangement for providing financial assistance to those affected. 2. Food, water and fodder should immediately be sent to all these areas to save the people and cattle.

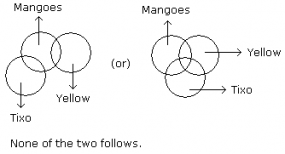
A. Only I follows B. Only II follows C. Either I or II follows D. Both I and II follow

Answer - Option B
Explanation - In t he break-out of a natural calamity, the basic duty of the government becomes to provide the basic amenities essential to save the lives of people and cattle. Providing financial assistance to all would put undue burden on the country's resources. So, only II follows.
31. Statement: Exporters in the capital are alleging that commercial banks are violating a Reserve Bank of India directive to operate a post shipment export credit denominated in foreign currency at international rates from January this year. Courses of Action: 1. The officers concerned in the commercial banks are to be suspended. 2. The RBI should be asked to stop giving such directives to commercial banks.

A. Only I follows B. Only II follows C. Either I or II follows D. Neither I nor II follows

Answer - Option D
Explanation - The statement mentions that the commercial banks violate a directive issued by the RBI. The remedy is only to make the banks implement the Act. So, none of the courses follows.
32. In the figure given below, square represents doctors, triangle represents ladies and circle represents surgeon. By which letter the ladies who doctor and surgeon both are represented ?

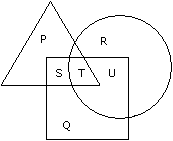
A. U B. T C. S D. P

Answer - Option B
33. SAB, ?, QCD, PDD, OEF, NFF

A. CBT B. ABR C. BCT D. RBB

Answer - Option D
Explanation - First letter in every group is in reverse alphabetical order i.e. SRQPON. The middle letter is in alphabetical order i.e ABCDEF and the last letter has pairs, BB, DD & FF.
34. If the letters of the word 'CYCLINDER' are arranged alphabetically, then which letter would be farthest from the first letter of word?

A. N B. E C. Y D. R

Answer - Option C
Explanation - Last letter is ‘Y’.
35. In a certain code 'CERTAIN' is coded as 'BFQUZJM'. How is 'MUNDANE' coded in that code?

A. LVMEZOD B. NTCOMBF C. NTOCNBF D. LTMCZOF

Answer - Option A
Explanation -Each letter moves -1, +1 alternately. So, M - 1 = L, U + 1 = V and so on. So code for MUNDANE will be LVMEZOD