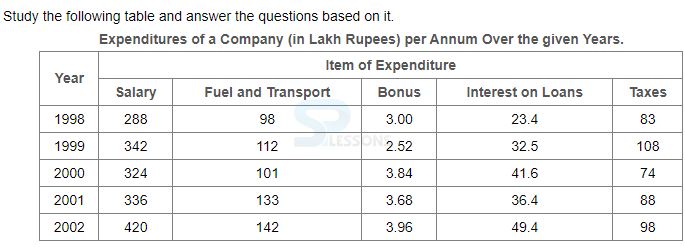
Directions (1-2):

1. What is the average amount of interest per year which the company had to pay during this period

A. Rs. 32.43 lakhs
B. Rs. 33.72 lakhs
C. Rs. 34.18 lakhs
D. Rs. 36.66 lakhs

Answer - Option D
Explanation - Average amount of interest paid by the Company during the given period
= Rs.[latex]\frac {23.4 + 32.5 + 41.6 + 36.4 + 49.4}{5}[/latex]Lakhs
= Rs.[latex]\frac {183.3}{5}[/latex]Lakhs
= Rs. 36.66 lakhs.
2. The total expenditure of the company over these items during the year 2000 is?

A. Rs. 544.44 lakhs
B. Rs. 501.11 lakhs
C. Rs. 446.46 lakhs
D. Rs. 478.87 lakhs

Answer - Option A
Explanation - Total expenditure of the Company during 2000
= Rs. (324 + 101 + 3.84 + 41.6 + 74) lakhs
= Rs. 544.44 lakhs.

1. On selling 17 balls at Rs. 720, there is a loss equal to the cost price of 5 balls. What is the cost price of a ball?

A. Rs. 55
B. Rs. 60
C. Rs. 34
D. Rs. 43

Answer - Option B
Explanation - loss = (cost price of 17 balls - selling price of 17 balls)
= (cost price of 17 balls - 720 )
⇒ (cost price of 17 balls - 720) = cost price of 5 balls
⇒ cost price of 12 balls = 720
⇒ cost price of 1 ball = 60
2. A trader mixes 26 kg of rice at Rs. 20 per kg with 30 kg of rice of other variety at Rs. 36 per kg and sells the mixture at Rs. 30 per kg. What is his profit percentage?

A. 6%
B. 7%
C. 4%
D. 5%

Answer - Option D
Explanation - cost price of 26 kg rice of first variety= 26 × 20= 520
cost price of 30 kg rice of second variety= 30 × 36= 1080
cost price of the 56 kg rice mixture= 520 + 1080= 1600
selling price of the 56 kg rice mixture= 56 × 30= 1680
profit = 1680 − 1600= 80
profit percentage = [latex]\frac {80\times100}{1600}[/latex] = 5%

1. P can finish a work in 18 days. Q can finish the same work in 15 days. Q worked for 10 days and left the job. how many days does P alone need to finish the remaining work?

A. 6
B. 4
C. 5
D. 8

Answer - Option A
Explanation - Work done by P in 1 day = [latex]\frac {1}{18}[/latex]
Work done by Q in 1 day = [latex]\frac {1}{15}[/latex]
Work done by Q in 10 days =[latex]\frac {10}{15}[/latex] = [latex]\frac {2}{3}[/latex]
Remaining work = 1 - [latex]\frac {2}{3}[/latex] = [latex]\frac {1}{3}[/latex]
Number of days in which P can finish the remaining work = [latex]\frac {1}{3}[/latex]/[latex]\frac {1}{18}[/latex] = 6
2. Anil and Suresh are working on a special assignment. Anil needs 6 hours to type 32 pages on a computer and Suresh needs 5 hours to type 40 pages. If both of them work together on two different computers, how much time is needed to type an assignment of 110 pages?

A. 7 hour 30 minutes
B. 8 hour 15 minutes
C. 7 hour 15 minutes
D. 8 hour 30 minutes

Answer - Option B
Explanation - Pages typed by Anil in 1 hour = [latex]\frac {32}{6}[/latex] = [latex]\frac {16}{3}[/latex]
Pages typed by Suresh in 1 hour = [latex]\frac {40}{5}[/latex] = 8
Pages typed by Anil and Suresh in 1 hour = [latex]\frac {16}{3}[/latex] + 8 = [latex]\frac {40}{3}[/latex]
Time taken to type 110 pages when Anil and Suresh work together = 110 × [latex]\frac {3}{40}[/latex]
= [latex]{8}^{1/4}[/latex] hours = 8 hour 15 minutes

1. A man takes 5 hours 45 min in walking to a certain place and riding back. He would have gained 2 hours by riding both ways. The time he would take to walk both ways is

A. 8 hrs 45 min
B. 11 hrs
C. 7 hrs 45 min
D. 9 hrs 20 min

Answer - Option C
Explanation - Given that time taken for riding both ways will be 2 hours lesser than the time needed for waking
one way and riding back.
Therefore, the time needed for riding one way = time needed for waking one way - 2 hours Given that time taken in walking one way and riding back = 5 hours 45 min
Hence, the time he would take to walk both ways
= 5 hours 45 min + 2 hours
= 7 hours 45 min
2. A man complete a journey in 10 hours. He travels first half of the journey at the rate of 21 km/hr and second half at the rate of 24 km/hr. Find the total journey in km.

A. 112 km
B. 121 km
C. 242 km
D. 224 km

Answer - Option D
Explanation - Average Speed =[latex]\frac {2\times21\times24}{21 + 24}[/latex] = 22.4 km/hr
Total distance = 22.4 × 10 = 224 km

1. A man has some hens and cows. If the number of heads be 48 and the number of feet equals 140, then the number of hens will be

A. 22
B. 24
C. 20
D. 26

Answer - Option D
Explanation - Let number of hens = h
number of cows = c
Number of heads = 48
⇒ h + c = 48 ⋯(1)
Number of feet = 140
⇒ 2h + 4c=140
⇒ h + 2c
= 70 ⋯(2)
(2)−(1) gives
2C− C=70−48
⇒ C = 22
i.e., number of hens = 26
2. To fill a tank, 25 buckets of water is required. How many buckets of water will be required to fill the same tank if the capacity of the bucket is reduced to two-fifth of its present?

A. 63
B. 64.5
C. 60.5
D. 62.5

Answer - Option D
Explanation - Let capacity of a bucket =1
Then, the capacity of the tank =25
New capacity of a bucket = [latex]\frac {2}{5}[/latex]
Hence, number of buckets required = [latex]\frac {25}{2/5}[/latex] = 62.5

1. If Rs. 10 be allowed as true discount on a bill of Rs. 110 due at the end of a certain time, then the discount allowed on the same sum due at the end of double the time is:

A. Rs. 20
B. Rs. 21.81
C. Rs. 22
D. Rs. 18.33

Answer - Option D
Explanation -S.I. on Rs. (110 - 10) for a certain time = Rs. 10.
S.I. on Rs. 100 for double the time = Rs. 20.
T.D. on Rs. 120 = Rs. (120 - 100) = Rs. 20.
T.D. on Rs. 110 = Rs [latex]\frac {20}{120}[/latex] [latex]\times[/latex] 100 =18.33
2. A man buys a watch for Rs. 1950 in cash and sells it for Rs. 2200 at a credit of 1 year. If the rate of interest is 10% per annum, the man:

A. gains Rs. 55
B. gains Rs. 50
C. loses Rs. 30
D. gains Rs. 30

Answer - Option B
Explanation - S.P. = P.W. of Rs. 2200 due 1 year hence
= Rs. [latex]\frac {2200 \times100}{100 + 10 \times 1}[/latex]
= Rs. 2000.
Gain = Rs. (2000 - 1950) = Rs. 50.

1. Find a positive number which when increased by 17 is equal to 60 times the reciprocal of the number.

A. 3
B. 10
C. 17
D. 20

Answer - Option A
Explanation -Let the number be x.
Then, x + 17 = [latex]\frac {60}{X}[/latex]
=> [latex]{X}^{2}[/latex] + 17x - 60 = 0
=> (x + 20)(x - 3) = 0
=> x = 3.
2. The sum of the digits of a two-digit number is 15 and the difference between the digits is 3. What is the two-digit number?

A. 69
B. 78
C. 96
D. Cannot be determined

Answer - Option D
Explanation - Let the ten's digit be x and unit's digit be y.
Then, x + y = 15 and x - y = 3 or y - x = 3.
Solving x + y = 15 and x - y = 3, we get: x = 9, y = 6.
Solving x + y = 15 and y - x = 3, we get: x = 6, y = 9.
So, the number is either 96 or 69.
Hence, the number cannot be determined.

1. The perimeter of a triangle is 28 cm and the inradius of the triangle is 2.5 cm. What is the area of the triangle?

A. 35[latex]{cm}^{2}[/latex]
B. 42[latex]{cm}^{2}[/latex]
C. 49[latex]{cm}^{2}[/latex]
D. [latex]70{cm}^{2}[/latex]

Answer - Option A
Explanation - Area of a triangle = [latex]r\times s[/latex]
here r is the inradius and s is the semi perimeter of the triangle.
Area of triangle = 2.5 [latex]\times[/latex] 28/2 = 35[latex]{cm}^{2}[/latex]
2. The area of a square is equal to five times the area of a rectangle of dimensions 125 cm * 64 cm. What is the perimeter of the square?

A. 600cm
B. 800cm
C. 400
D. 1000

Answer - Option B
Explanation -Area of the square = s * s = 5(125 * 64)
=> s = 25 * 8 = 200 cm
Perimeter of the square = 4 * 200 = 800 cm.

1. What decimal of an hour is a second ?

A. .0025
B. .0256
C. .00027
D. .000126

Answer - Option C
Explanation - Required decimal = [latex]\frac {1}{60\times60}[/latex] = [latex]\frac {1}{3600}[/latex] = .00027
2. The price of commodity X increases by 40 paise every year, while the price of commodity Y increases by 15 paise every year. If in 2001, the price of commodity X was Rs. 4.20 and that of Y was Rs. 6.30, in which year commodity X will cost 40 paise more than the commodity Y ?

A. 2010
B.2011
C.2012
D.2013

Answer - Option B
Explanation -Suppose commodity X will cost 40 paise more than Y after z years.
Then, (4.20 + 0.40z) - (6.30 + 0.15z) = 0.40
=> 0.25z = 0.40 + 2.10
=> z = [latex]\frac {2.50}{0.25}[/latex] = [latex]\frac {250}{25}[/latex] = 10
X will cost 40 paise more than Y 10 years after 2001 i.e., 2011.

1. A grocer has a sale of Rs. 6435, Rs. 6927, Rs. 6855, Rs. 7230 and Rs. 6562 for 5 consecutive months. How much sale must he have in the sixth month so that he gets an average sale of Rs. 6500?

A. Rs. 4991
B. Rs. 5991
C. Rs. 6001
D. Rs. 6991

Answer - Option A
Explanation - Total sale for 5 months = Rs. (6435 + 6927 + 6855 + 7230 + 6562) = Rs. 34009.
Required sale = Rs. [ (6500 x 6) - 34009 ]
= Rs. (39000 - 34009)
= Rs. 4991.
2. The average of 20 numbers is zero. Of them, at the most, how many may be greater than zero?

A. 0
B. 1
C. 10
D. 19

Answer - Option D
Explanation - Average of 20 numbers = 0.
Sum of 20 numbers (0 x 20) = 0.
It is quite possible that 19 of these numbers may be positive and if their sum is a then 20th number is (-a).