Directions to Solve: Below in each of the questions are given two statements I and II. These statements may be either independent causes or may be effects of independent causes or a common cause. One of these statements may be the effect of the other statements. Read both the statements and decide which of the following answer choice correctly depicts the relationship between these two statements.
Mark answer

A. If statement I is the cause and statement II is its effect. B. If statement II is the cause and statement I is its effect. C. If both the statements I and II are independent causes. D. If both the statements I and II are effects of independent causes. E. If both the statements I and II are effects of some common cause.

1. Statements:

I. Standard of living among the middle class society is constantly going up since part of few years. II. Indian Economy is observing remarkable growth.

A. Statement I is the cause and statement II is its effect. B. Statement II is the cause and statement I is its effect. C. Both the statements I and II are independent causes. D. Both the statements I and II are effects of independent causes. E. Both the statements I and II are effects of some common cause.

Answer: Option A
2. Statements:

I. The meteorological Department has issued a statement mentioning deficient rainfall during monsoon in many parts of the country. II. The Government has lowered the revised estimated GDP growth from the level of earlier estimates.

A. Statement I is the cause and statement II is its effect. B. Statement II is the cause and statement I is its effect. C. Both the statements I and II are independent causes. D. Both the statements I and II are effects of independent causes. E. Both the statements I and II are effects of some common cause.

Answer: Option D
3. Statements:

I. The staff of Airport Authorities called off the strike they were observing in protest against privatization. II. The staff of Airport Authorities went on strike anticipating a threat to their jobs.

A. Statement I is the cause and statement II is its effect. B. Statement II is the cause and statement I is its effect. C. Both the statements I and II are independent causes. D. Both the statements I and II are effects of independent causes. E. Both the statements I and II are effects of some common cause.

Answer: Option D
4.Statements:

I. A huge truck overturned on the middle of the road last night. II. The police had cordoned of entire area in the locality this morning for half of the day.

A. Statement I is the cause and statement II is its effect. B. Statement II is the cause and statement I is its effect. C. Both the statements I and II are independent causes. D. Both the statements I and II are effects of independent causes. E. Both the statements I and II are effects of some common cause.

Answer: Option A
5. Statements:

I. Importance of Yoga and exercise is being realized by all sections of the society. II. There is an increasing awareness about health in the society particularly among middle ages group of people.

A. Statement I is the cause and statement II is its effect. B. Statement II is the cause and statement I is its effect. C. Both the statements I and II are independent causes. D. Both the statements I and II are effects of independent causes. E. Both the statements I and II are effects of some common cause.

Answer: Option B

Directions to Solve In each question below are given two statements followed by two conclusions numbered I and II. You have to take the given two statements to be true even if they seem to be at variance from commonly known facts. Read the conclusion and then decide which of the given conclusions logically follows from the two given statements, disregarding commonly known facts.
Give answer:

A. If only conclusion I follows B. If only conclusion II follows C. If either I or II follows D. If neither I nor II follows and E. If both I and II follow.

1. Statements: No women teacher can play. Some women teachers are athletes. Conclusions: I. Male athletes can play. II. Some athletes can play.

A. Only conclusion I follows B. Only conclusion II follows C. Either I or II follows D. Neither I nor II follows E. Both I and II follow

Answer: Option D
2. Statements: All bags are cakes. All lamps are cakes. Conclusions: I. Some lamps are bags. II. No lamp is bag.

A. Only conclusion I follows B. Only conclusion II follows C. Either I or II follows D. Neither I nor II follows E. Both I and II follow

Answer: Option C
3. Statements: All mangoes are golden in colour. No golden-coloured things are cheap. Conclusions: I. All mangoes are cheap. II. Golden-coloured mangoes are not cheap.

A. Only conclusion I follows B. Only conclusion II follows C. Either I or II follows D. Neither I nor II follows E. Both I and II follow

Answer: Option B
4. Statements: Some kings are queens. All queens are beautiful. Conclusions: I. All kings are beautiful. II. All queens are kings.

A. Only conclusion I follows B. Only conclusion II follows C. Either I or II follows D. Neither I nor II follows E. Both I and II follow

Answer: Option D
5. Statements: Some doctors are fools. Some fools are rich. Conclusions: I. Some doctors are rich II. Some rich are doctors.

A. Only conclusion I follows B. Only conclusion II follows C. Either I or II follows D. Neither I nor II follows E. Both I and II follow

Answer: Option D

Directions 1 : Study the following information carefully and answer the questions given below: Four friends Amrita, Deepa, Smita and Rhea complete their PhD in different number of years. The one who took maximum time took eight years to complete her PhD while the one who took the least time took only three years to complete it. Rhea took more time only than Amrita and completed her PhD in five years. Smita did not take longer time than Deepa to complete her PhD.
1. How many years did Amrita take to complete her PhD?

A. 8 B. 3 C. 4 D. Either 6 or 7 E. Cannot be determined

Answer: Option B
2. How many years did Smita take to complete her PhD ?

A. 8 B. 3 C. 4 D. 7 E. Cannot be determined

Answer: Option D
3. Who amongst the following took the maximum number of years to complete PhD ?

A. Amrita B. Rhea C. Smita D. Deepa E. Cannot be determined

Answer: Option D
4. How many meaningful English words can be formed with the letters TEID using each letter only once in each word?

A. None B. One C. Two D. Three E. More than three

Answer: Option D
5. If it is possible to make only one meaningful word with the second, fifth, eighth and the eleventh letters (when counted from left hand side) of the word DEVELOPMENT, which would be the second letter of the word from the left ? If more than one such word can be formed, give X as the answer. If no such word can be formed, give Z as your answer.

A. E B. L C. T D. X E. Z

Answer: Option A

Directions to Solve In each of the questions below consists of a question and two statements numbered I and II given below it. You have to decide whether the data provided in the statements are sufficient to answer the question. Read both the statements and Give answer

A. If the data in statement I alone are sufficient to answer the question, while the data in statement II alone are not sufficient to answer the question B. If the data in statement II alone are sufficient to answer the question, while the data in statement I alone are not sufficient to answer the question C. If the data either in statement I alone or in statement II alone are sufficient to answer the question D. If the data given in both statements I and II together are not sufficient to answer the question and E. If the data in both statements I and II together are necessary to answer the question.

1. Question: In which year was Rahul born? Statements: I. Rahul at present is 25 years younger to his mother. II. Rahul's brother, who was born in 1964, is 35 years younger to his mother.

A. I alone is sufficient while II alone is not sufficient B. II alone is sufficient while I alone is not sufficient C. Either I or II is sufficient D. Neither I nor II is sufficient E. Both I and II are sufficient

Answer: Option E
2. Question: What will be the total weight of 10 poles, each of the same weight? Statements: I. One-fourth of the weight of each pole is 5 kg. II. The total weight of three poles is 20 kilograms more than the total weight of two poles.

A. I alone is sufficient while II alone is not sufficient B. II alone is sufficient while I alone is not sufficient C. Either I or II is sufficient D. Neither I nor II is sufficient E. Both I and II are sufficient

Answer: Option C
3. Question: How many children does M have? Statements:

I. H is the only daughter of X who is wife of M. II. K and J are brothers of M. A. I alone is sufficient while II alone is not sufficient B. II alone is sufficient while I alone is not sufficient C. Either I or II is sufficient D. Neither I nor II is sufficient E. Both I and II are sufficient

Answer: Option D
4. Question: How much was the total sale of the company? Statements: I. The company sold 8000 units of product A each costing Rs. 25. II. This company has no other product line.

A. I alone is sufficient while II alone is not sufficient B. II alone is sufficient while I alone is not sufficient C. Either I or II is sufficient D. Neither I nor II is sufficient E. Both I and II are sufficient

Answer: Option E
5. Question: The last Sunday of March, 2006 fell on which date? Statements: I. The first Sunday of that month fell on 5th. II. The last day of that month was Friday.

A. I alone is sufficient while II alone is not sufficient B. II alone is sufficient while I alone is not sufficient C. Either I or II is sufficient D. Neither I nor II is sufficient E. Both I and II are sufficient

Answer: Option C

Directions to Solve Read each definition and all four choices carefully, and find the answer that provides the best example of the given definition.
1. Applying for Seasonal Employment occurs when a person requests to be considered for a job that is dependent on a particular season or time of year. Which situation below is the best example of Applying for Seasonal Employment?

A. The ski instructors at Top of the Peak Ski School work from December through March. B. Matthew prefers jobs that allow him to work outdoors. C. Lucinda makes an appointment with the beach resort restaurant manager to interview for the summer waitressing position that was advertised in the newspaper. D. Doug's ice cream shop stays open until 11 p.m. during the summer months.

Answer: Option C
2. Violating an Apartment Lease occurs when a tenant does something prohibited by the legally binding document that he or she has signed with a landlord. Which situation below is the best example of violating an Apartment Lease?

A. Tim has decided to move to another city, so he calls his landlord to tell him that he is not interested in renewing his lease when it expires next month. B. Valerie recently lost her job and, for the last three months, has neglected to pay her landlord the monthly rent they agreed upon in writing when she moved into her apartment eight months ago. C. Mark writes a letter to his landlord that lists numerous complaints about the apartment he has agreed to rent for two years. D. Leslie thinks that her landlord is neglecting the building in which she rents an apartment. She calls her attorney to ask for advice.

Answer: Option B
3. An Informal Gathering occurs when a group of people get together in a casual, relaxed manner. Which situation below is the best example of an Informal Gathering?

A. The book club meets on the first Thursday evening of every month. B. After finding out about his promotion, Jeremy and a few coworkers decide to go out for a quick drink after work. C. Mary sends out 25 invitations for the bridal shower she is giving for her sister. D. Whenever she eats at the Mexican restaurant, Clara seems to run into Peter.

Answer: Option B
4. People speculate when they consider a situation and assume something to be true based on inconclusive evidence. Which situation below is the best example of Speculation?

A. Francine decides that it would be appropriate to wear jeans to her new office on Friday after reading about "Casual Fridays" in her employee handbook. B. Mary spends thirty minutes sitting in traffic and wishes that she took the train instead of driving. C. After consulting several guidebooks and her travel agent, Jennifer feels confident that the hotel she has chosen is first-rate. D. When Emily opens the door in tears, Theo guesses that she's had a death in her family.

Answer: Option D
5. Posthumous Publication occurs when a book is published after the author's death. Which situation below is the best example of Posthumous Publication?

A. Richard's illness took his life before he was able to enjoy the amazing early reviews of his novel. B. Melissa's publisher cancels her book contract after she fails to deliver the manuscript on time. C. Clarence never thought he'd live to see the third book in his trilogy published. D. Elizabeth is honored with a prestigious literary award for her writing career and her daughter accepts the award on behalf of her deceased mother.

Answer: Option A

Directions to Solve: In these series, you will be looking at both the letter pattern and the number pattern. Fill the blank in the middle of the series or end of the series.
1. SCD, TEF, UGH, ____, WKL

A. CMN B. UJI C. VIJ D. IJT

Answer: Option C
2. B2CD, _____, BCD4, B5CD, BC6D

A. B2C2D B. BC3D C. B2C3D D. BCD7

Answer: Option B
3. FAG, GAF, HAI, IAH, ____

A. JAK B. HAL C. HAK D. JAI

Answer: Option A
4. ELFA, GLHA, ILJA, _____, MLNA

A. OLPA B. KLMA C. LLMA D. KLLA

Answer: Option D
5. CMM, EOO, GQQ, _____, KUU

A. GRR B. GSS C. ISS D. ITT

Answer: Option C

Directions to Solve Each question has an underlined word followed by four answer choices. You will choose the word that is a necessary part of the underlined word.
1. harvest

A. autumn B. stockpile C. tractor D. crop

Answer: Option D
2. desert

A. cactus B. arid C. oasis D. flat

Answer: Option B
3. book

A. fiction B. pages C. pictures D. learning

Answer: Option B
4. language

A. tongue B. slang C. writing D. words

Answer: Option D
5. school

A. student B. report card C. test D. learning

Answer: Option A

Directions to Solve First, you will be given a list of three "nonsense" words and their English word meanings. The question(s) that follow will ask you to reverse the process and translate an English word into the artificial language.
1. Here are some words translated from an artificial language. gorblflur means fan belt pixngorbl means ceiling fan arthtusl means tile roof Which word could mean "ceiling tile"?

A. gorbltusl B. flurgorbl C. arthflur D. pixnarth

Answer: Option D
2. Here are some words translated from an artificial language. hapllesh means cloudburst srenchoch means pinball resbosrench means ninepin Which word could mean "cloud nine"?

A. leshsrench B. ochhapl C. haploch D. haplresbo

Answer: Option D
3. Here are some words translated from an artificial language. agnoscrenia means poisonous spider delanocrenia means poisonous snake agnosdeery means brown spider Which word could mean "black widow spider"?

A. deeryclostagnos B. agnosdelano C. agnosvitriblunin D. trymuttiagnos

Answer: Option C
4. Here are some words translated from an artificial language. moolokarn means blue sky wilkospadi means bicycle race moolowilko means blue bicycle Which word could mean "racecar"?

A. wilkozwet B. spadiwilko C. moolobreil D. spadivolo

Answer: Option D
5. Here are some words translated from an artificial language. migenlasan means cupboard lasanpoen means boardwalk cuopdansa means pullman Which word could mean "walkway"?

A. poenmigen B. cuopeisel C. lasandansa D. poenforc

Answer: Option D

Directions to Solve: Study the following table and answer the questions based on it.

1. What is the average amount of interest per year which the company had to pay during this period?

A. Rs. 32.43 lakhs B. Rs. 33.72 lakhs C. Rs. 34.18 lakhs D. Rs. 36.66 lakhs

Answer: Option D
Explanation: Average amount of interest paid by the Company during the given period = Rs. [latex][\frac{23.4 + 32.5 + 41.6 + 36.4 + 49.4}{5}][/latex] lakhs = Rs. [latex][\frac{183.3}{5}][/latex] lakhs = Rs. 36.66 lakhs.
2. The total amount of bonus paid by the company during the given period is approximately what percent of the total amount of salary paid during this period?

A. 0.1% B. 0.5% C. 1% D. 1.25%

Answer: Option C
Explanation: Required percentage = [latex][\frac{(3.00 + 2.52 + 3.84 + 3.68 + 3.96)}{(288 + 342 + 324 + 336 + 420)}*100][/latex] % = [latex][\frac{17}{1710}*100][/latex] % =1 %
3. Total expenditure on all these items in 1998 was approximately what percent of the total expenditure in 2002?

A. 62% B. 66% C. 69% D. 71%

Answer: Option C
Explanation: Required percentage = [latex][\frac{(288 + 98 + 3.00 + 23.4 + 83)}{(420 + 142 + 3.96 + 49.4 + 98)}*100][/latex] % = [latex][\frac{495.4}{713.36}*100][/latex] % =69.45 %
4. The total expenditure of the company over these items during the year 2000 is?

A. Rs. 544.44 lakhs B. Rs. 501.11 lakhs C. Rs. 446.46 lakhs D. Rs. 478.87 lakhs

Answer: Option A
Explanation: Total expenditure of the Company during 2000 = Rs. (324 + 101 + 3.84 + 41.6 + 74) lakhs = Rs. 544.44 lakhs.
5.The ratio between the total expenditure on Taxes for all the years and the total expenditure on Fuel and Transport for all the years respectively is approximately?

A. 4:7 B. 10:13 C. 15:18 D. 5:8

Answer: Option B Explanation: Required ratio = [latex][\frac{(83 + 108 + 74 + 88 + 98)}{(98 + 112 + 101 + 133 + 142)}][/latex] = [latex][\frac{451}{586}][/latex] =[latex]\frac{1}{1.3}[/latex] =[latex]\frac{10}{13}[/latex]

Directions to Solve: Each problem consists of three statements. Based on the first two statements, the third statement may be true, false, or uncertain.
1. Tanya is older than Eric. Cliff is older than Tanya. Eric is older than Cliff. If the first two statements are true, the third statement is

A. true B. false C. uncertain

Answer: Option B
2. Blueberries cost more than strawberries. Blueberries cost less than raspberries. Raspberries cost more than strawberries and blueberries. If the first two statements are true, the third statement is

A. true B. false C. uncertain

Answer: Option A
3. All the trees in the park are flowering trees. Some of the trees in the park are dogwoods. All dogwoods in the park are flowering trees. If the first two statements are true, the third statement is

A. true B. false C. uncertain

Answer: Option A
4. Mara runs faster than Gail. Lily runs faster than Mara. Gail runs faster than Lily. If the first two statements are true, the third statement is

A. true B. false C. uncertain

Answer: Option B
5. Apartments in the Riverdale Manor cost less than apartments in The Gaslight Commons. Apartments in the Livingston Gate cost more than apartments in the The Gaslight Commons. Of the three apartment buildings, the Livingston Gate costs the most. If the first two statements are true, the third statement is

A. true B. false C. uncertain

Answer: Option A

Directions to Solve: A good way to figure out the relationship in a given question is to make up a sentence that describes the relationship between the first two words. Then, try to use the same sentence to find out which of the answer choices completes the same relationship with the third word.
1. Odometer is to mileage as compass is to

A. speed B. hiking C. needle D. direction

Answer: Option D
2. Marathon is to race as hibernation is to

A. winter B. bear C. dream D. sleep

Answer: Option D
3. Window is to pane as book is to

A. novel B. glass C. cover D. page

Answer: Option D
4. Cup is to coffee as bowl is to

A. dish B. soup C. spoon D. food

Answer: Option B
5. Yard is to inch as quart is to

A. gallon B. ounce C. milk D. liquid

Answer: Option B

Directions to Solve: Each question presents a situation and asks you to make a judgment regarding that particular circumstance. Choose an answer based on given information.
1. Eileen is planning a special birthday dinner for her husband's 35th birthday. She wants the evening to be memorable, but her husband is a simple man who would rather be in jeans at a baseball game than in a suit at a fancy restaurant. Which restaurant below should Eileen choose?

A. Alfredo's offers fine Italian cuisine and an elegant Tuscan decor. Patrons will feel as though they've spent the evening in a luxurious Italian villa. B. Pancho's Mexican Buffet is an all-you-can-eat family style smorgasbord with the best tacos in town. C. The Parisian Bistro is a four-star French restaurant where guests are treated like royalty. Chef Dilbert Olay is famous for his beef bourguignon. D. Marty's serves delicious, hearty meals in a charming setting reminiscent of a baseball clubhouse in honor of the owner, Marty Lester, a former major league baseball all-star.

Answer: Option D
2. The film director wants an actress for the lead role of Lucy who perfectly fits the description that appears in the original screenplay. He is not willing to consider actresses who do not resemble the character as she is described in the screenplay, no matter how talented they are. The screenplay describes Lucy as an average-sized, forty something redhead, with deep brown eyes, very fair skin, and a brilliant smile. The casting agent has four actresses in mind. Actress #1 is a stunning red-haired beauty who is 5'9" and in her mid-twenties. Her eyes are brown and she has an olive complexion. Actress #2 has red hair, big brown eyes, and a fair complexion. She is in her mid-forties and is 5'5". Actress #3 is 5'4" and of medium build. She has red hair, brown eyes, and is in her early forties. Actress #4 is a blue-eyed redhead in her early thirties. She's of very slight build and stands at 5'.

A. 1, 2 B. 2, 3 C. 1, 4 D. 2, 4

Answer: Option B
3. The school principal has received complaints from parents about bullying in the school yard during recess. He wants to investigate and end this situation as soon as possible, so he has asked the recess aides to watch closely. Which situation should the recess aides report to the principal?

A. A girl is sitting glumly on a bench reading a book and not interacting with her peers. B. Four girls are surrounding another girl and seem to have possession of her backpack. C. Two boys are playing a one-on-one game of basketball and are arguing over the last basket scored. D. Three boys are huddled over a handheld video game, which isn't supposed to be on school grounds.

Answer: Option B
4. Mrs. Carson took a taxi to meet her three friends for lunch. They were waiting for her outside the restaurant when she pulled up in the car. She was so excited to see her friends that she left her tote bag in the taxi. As the taxi pulled away, she and her friends took notice of the license plate number so they would be able to identify the car when they called the taxi company.

#1: The four women seem to agree that the plate starts out with the letter J. #2: Three of them agree that the plate ends with 12L. #3: Three of them think that the second letter is X, and a different three think that the third letter is K.

The four license plate numbers below represent what each of the four women thinks she saw. Which one is most likely the license plate number of the taxi?

A. JXK 12L B. JYK 12L C. JXK 12I D. JXX 12L

Answer: Option A
5. Zachary has invited his three buddies over to watch the basketball game on his wide-screen television. They are all hungry, but no one wants to leave to get food. Just as they are arguing about who should make the food run, a commercial comes on for a local pizze-ria that delivers. The phone number flashes on the screen briefly and they all try to remember it. By the time Zachary grabs a pen and paper, each of them recollects a different number.

#1: All of the men agree that the first three numbers are 995. #2: Three of them agree that the fourth number is 9. #3: Three agree that the fifth number is 2. #4: Three agree that the sixth number is 6; three others agree that the seventh number is also 6.

Which of the numbers is most likely the telephone number of the pizzeria?

A. 995-9266 B. 995-9336 C. 995-9268 D. 995-8266

Answer: Option A

Directions to Solve: Each of the following questions contains a small paragraph followed by a question on it. Read each paragraph carefully and answer the question given below it.
1. The attainment of individual and organisational goals is mutually interdependent and linked by a common denominator - employee work motivation. Organisational members are motivated to satisfy their personal goals, and they contribute their efforts to the attainment of organisational objectives as means of achieving these personal goals. The passage best supports the statement that motivation -

A. encourages an individual to give priority to personal goals over organisational goals. B. is crucial for the survival of an individual and organisation. C. is the product of an individual's physical and mental energy. D. is the external force which induces an individual to contribute his efforts. E. makes organisation and society inseparable.

Answer: Option A
2. Due to enormous profits involved in smuggling, hundreds of persons have been attracted towards this anti-national activity. Some of them became millionaires overnight. India has a vast coastline both on the Eastern and Western Coast. It has been a heaven for smugglers who have been carrying on their activities with great impunity. There is no doubt, that from time to time certain seizures were made by the enforcement authorities, during raids and ambush but even allowing these losses the smugglers made huge profits. The passage best supports the statement that

A. smuggling hampers the economic development of a nation. B. smuggling ought to be curbed. C. authorities are taking strict measures to curb smuggling. D. smuggling is fast increasing in our country owing to the quick profit it entails.

Answer: Option D
3. Though the waste of time or the expenditure on fashions is very large, yet fashions have come to stay. They will not go, come what may. However, what is now required is that strong efforts should be made to displace the excessive craze for fashion from the minds of these youngsters. The passage best supports the statement that:

A. fashion is the need of the day. B. the excessive craze for fashion is detrimental to one's personality. C. the hoard for fashion should be done away with so as not to let down the constructive development. D. work and other activities should be valued more than the outward appearance.

Answer: Option C
4. One of the important humanitarian by-products of technology is the greater dignity and value that it imparts to human labour. In a highly industrialized society, there is no essential difference between Brahmin and Dalit, Muslim and Hindu; they are equally useful and hence equally valuable for in the industrial society individual productivity fixes the size of the pay cheque and this fixes social status. The passage best supports the statement that:

A. technology decides individual's social status. B. castes and religions are man-made. C. human labour has dignity and value. D. all individuals, irrespective of caste and creed, are born equal. E. industrial society is a great leveller of men.

Answer: Option C
5. The future of women in India is quite bright and let us hope that they will justify their abilities by rising to the occasion. Napoleon was right when he declared that by educating the women we can educate the whole nation. Because a country can never rise without the contribution of 50% of their population. The passage best supports the statement that:

A. India is striving hard for the emancipation of women. B. all women should be well educated. C. a nation can progress only when women are given equal rights and opportunities as men. D. women ought to be imparted full freedom to prove their worth and contribute to the progress of the nation.

Answer: Option D

Directions to Solve: Three of the words will be in the same classification, the remaining one will not be. Your answer will be the one word that does NOT belong in the same classification as the others.
1. Which word does NOT belong with the others?

A. parsley B. basil C. dill D. mayonnaise

Answer: Option D
2. Which word does NOT belong with the others?

A. inch B. ounce C. centimeter D. yard

Answer: Option B
3. Which word does NOT belong with the others?

A. tyre B. steering wheel C. engine D. car

Answer: Option D
4. Which word does NOT belong with the others?

A. tulip B. rose C. bud D. daisy

Answer: Option C
5. Which word does NOT belong with the others?

A. rye B. sourdough C. pumpernickel D. loaf

Answer: Option A

Directions to Solve: In each series, look for the degree and direction of change between the numbers. In other words, do the numbers increase or decrease, and by how much
1. Look at this series: 2, 1, (1/2), (1/4), ... What number should come next?

A. (1/3) B. (1/8) C. (2/8) D. (1/16)

Answer: Option B
2. Look at this series: 7, 10, 8, 11, 9, 12, ... What number should come next?

A. 7 B. 10 C. 12 D. 13

Answer: Option B
3. Look at this series: 36, 34, 30, 28, 24, ... What number should come next?

A. 20 B. 22 C. 23 D. 26

Answer: Option B
4. Look at this series: 22, 21, 23, 22, 24, 23, ... What number should come next?

A. 22 B. 24 C. 25 D. 26

Answer: Option C
5. Look at this series: 53, 53, 40, 40, 27, 27, ... What number should come next?

A. 12 B. 14 C. 27 D. 53

Answer: Option B

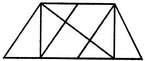
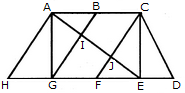
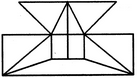
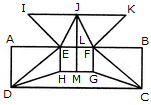
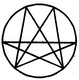
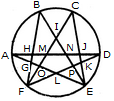
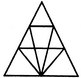
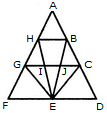
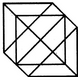
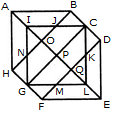
1. Find the number of triangles in the given figure.

A. 8 B. 10 C. 12 D. 14

Answer: Option D
Explanation: The figure may be labelled as shown. The simplest triangles are AHG, AIG, AIB, JFE, CJE and CED i.e. 6 in number. The triangles composed of two components each are ABG, CFE, ACJ and EGI i.e. 4 in number. The triangles composed of three components each are ACE, AGE and CFD i.e. 3 in number. There is only one triangle i.e. AHE composed of four components. Therefore, There are 6 + 4 + 3 + 1 = 14 triangles in the given figure.
2. Find the minimum number of straight lines required to make the given figure.

A. 16 B. 17 C. 18 D. 19

Answer: Option B
Explanation: The figure may be labelled as shown. The horizontal lines are IK, AB, HG and DC i.e. 4 in number. The vertical lines are AD, EH, JM, FG and BC i.e. 5 in number. The slanting lines are IE, JE, JF, KF, DE, DH, FC and GC i.e. 8 is number. Thus, there are 4 + 5 + 8 = 17 straight lines in the figure.
3. Find the number of triangles in the given figure.

A. 22 B. 24 C. 26 D. 28

Answer: Option D
Explanation: The figure may be labelled as shown. The simplest triangles are AGH, GFO, LFO, DJK, EKP, PEL and IMN i.e. 7 in number. The triangles having two components each are GFL, KEL, AMO, NDP, BHN, CMJ, NEJ and HFM i.e. 8 in number. The triangles having three components each are IOE, IFP, BIF and CEI i.e. 4 in number. The triangles having four components each are ANE and DMF i.e. 2 in number. The triangles having five components each are FCK, BGE and ADL i.e. 3 in number. The triangles having six components each are BPF, COE, DHF and AJE i.e. 4 in number. Total number of triangles in the figure = 7 + 8 + 4 + 2 + 3 + 4 = 28.
4. Find the number of triangles in the given figure.

A. 12 B. 18 C. 22 D. 26

Answer: Option B
Explanation: The figure may be labelled as shown. The simplest triangles are AHB, GHI, BJC, GFE, GIE, IJE, CEJ and CDE i.e. 8 in number. The triangles composed of two components each are HEG, BEC, HBE, JGE and ICE i.e. 5 in number. The triangles composed of three components each are FHE, GCE and BED i.e. 3 in number. There is only one triangle i.e. AGC composed of four components. There is only one triangle i.e. AFD composed of nine components. Thus, there are 8 + 5 + 3 + 1 + 1 = 18 triangles in the given figure.
5. Find the number of triangles in the given figure.

A. 18 B. 20 C. 24 D. 27

Answer: Option C
Explanation: The figure may be labelled as shown. The simplest triangles are IJO, BCJ, CDK, KQL, MLQ, GFM, GHN and NIO i.e. 8 in number. The triangles composed of two components each are ABO, AHO, NIJ, IGP, ICP, DEQ, FEQ, KLM, LCP and LGP i.e.10 in number. The triangles composed of four components each are HAB, DEF, LGI, GIC, ICL and GLC i.e. 6 in number. Total number of triangles in the figure = 8 + 10 + 6 = 24.