 Introduction
Introduction
APPSC FBO Main Exam – Practice Test section allows candidates to practice the learned material to ensure that the candidate understands the pattern of the exam and the expected questions that would appear in the actual test. The article APPSC FBO Mains Model Paper provides pattern of questions asked in APPSC FBO Mains with detailed solution. SPLessons made sincere effort to provide APPSC FBO Mains Model Paper.
 Pattern
Pattern
APPSC FBO Mains Exam Pattern
| S. No. | Subject | Marks | Questions | Duration |
|---|---|---|---|---|
| 1. | Writing an essay in English or Telugu or Urdu (Descriptive type) | 50 Marks(Qualifying Test) | 1 Question | 30 Minutes |
| 2. | Paper-1 General Studies & Mental Ability (Objective type) | 100 Marks | 100 Questions | 100 Minutes |
| 3. | Paper-2 General Science & General Mathematics (SSC standard)(Objective type) | 50 Marks(Qualifying Test) | 100 Questions | 100 Minutes |
| Total | 200 Marks |
 Syllabus
Syllabus
For FBO Mains Exam Detailed Syllabus: Click Here
 Samples
Samples
Write an essay on any one of the topics given below in about 1000 words.
A. Protection of Environment – Existence of Human beings.
B. Advantages and disadvantages of Internet.
C. Tourist places of Andhra Pradesh
Answer:
C. Tourist places of Andhra Pradesh:
Andhra Pradesh is a well-known Indian state for its beautiful culture and heritage where one can experience the natural beauty of landscapes, architecture, art and culture. Because of such beautiful experiences, Andhra Pradesh has enhanced image not only at the national level but also at the global level. Andhra Pradesh is the fifth-largest state in India and this state is surrounded by Karnataka in the west, Tamil Nadu in the south, Maharashtra in north and Odisha and Madhya Pradesh on north-east. This Indian state is famous for glorious past and you will explore the amazing ancient temples, palaces, monuments, forts and rich culture at this destination.
Andhra Pradesh tourism is one of famous place located in south India with many tourist places which make people joy and wonderful by seeing them. Now going into deep about Andhra Pradesh tourism main tourist places are Vizag beach, Vijayawada Durga temple and Nagarjuna Sagar, Charminar and many other.
1. AHOBILAM: it is located in district Kurnool and know as the capital of demon king hiranyakashipu father of bhakta Prahalad, a devotee of Sri Bhagwan Vishnu appeared here as Narashima and killed hiranya kashipu.it is only here Nava Narasimha is worshipped.
2. AMARAVATI: it is located in district Guntur, famous for Buddhist monuments on river Krishna. Acharya Nagarjuna constructed here the largest stupa 2000years back.
3. ANNAVARAM: it is located in district east Godavari and famous for Sri Satyanarayana Swamy temple.
4. Tirupati: it is located in district Chittoor and famous for Sri Venkateswara Swamy Temple
1. What is the total number of states in our country?
 77. How many male members are there in the family?
77. How many male members are there in the family?
 82. Towards which direction was the vehicle moving before it stopped at point Q?
82. Towards which direction was the vehicle moving before it stopped at point Q?
 84. Whose seat is between Q and S?
84. Whose seat is between Q and S?


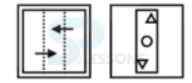
 94. How many persons sit between P and W when counted in the anti-clockwise direction from P?
94. How many persons sit between P and W when counted in the anti-clockwise direction from P?
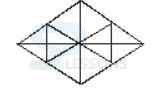
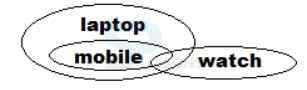 From the Venn diagram we can infer that conclusion I am definitely false. And as all mobile is a laptop and some mobile is watched we can say that some watches are laptop is true.
99. Statements:
No gentleman is poor.
All gentlemen are rich.
Conclusions:
I. No poor man is rich.
II. No rich man is poor.
Answer: Option D
Explanation:
From the Venn diagram we can infer that conclusion I am definitely false. And as all mobile is a laptop and some mobile is watched we can say that some watches are laptop is true.
99. Statements:
No gentleman is poor.
All gentlemen are rich.
Conclusions:
I. No poor man is rich.
II. No rich man is poor.
Answer: Option D
Explanation:
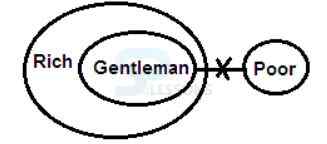 From the Venn diagram we can see that both the conclusions I and II are not true for all the cases. Hence both I and II do not follow.
100. Statements:
No magazine is cap.
All caps are cameras.
Conclusions:
I. No camera is magazine.
II. Some cameras are magazines.
Answer: Option C
Explanation:
From the Venn diagram we can see that both the conclusions I and II are not true for all the cases. Hence both I and II do not follow.
100. Statements:
No magazine is cap.
All caps are cameras.
Conclusions:
I. No camera is magazine.
II. Some cameras are magazines.
Answer: Option C
Explanation:
 From the Venn diagram we can see that after considering all the cases either conclusion I or II will be true.
From the Venn diagram we can see that after considering all the cases either conclusion I or II will be true.
-
A. 22
B. 25
C. 29
D. 30
-
A. Andhra Pradesh
B. Gujarat
C. Karnataka
D. Tamilnadu
-
A. Mango tree
B. Teak tree
C. Coconut tree
D. Neem tree
-
A. Visakahapatnam
B. Vijayawada
C. Warangal
D. Tirupati
-
A. Smriti Irani
B. Ravi Shankar Prasad
C. Jitendra Singh
D. Thawar Chand Gehlot
-
A. Vijayanagaram
B. Warangal
C. Hyderabad
D. Kurnool
-
A. Neelam sanjeeva reddy
B. Marri chenna reddy
C. Damodarm Sanjeeviah
D. Kasu Brahmananda reddy
-
A. Sri. K. Rosiah
B. Sri.N.D.Tiwari
C. Sri. E.S.L. Narasimhan
D. Biswabhusan Harichandan
-
A. 1918
B. 1926
C. 1954
D. 1826
-
A. 1939
B. 1914
C. 1918
D. 1845
-
A. Geneva
B. Washington
C. San Francisco
D. Rome
-
A. Alam Aara
B. Lava Kusa
C. Mogal- e- Azam
D. Bobby
-
A. 15 August 1947
B. 26 January 1950
C. 15 August 1958
D. 15 September 1959
-
A. 1959
B. 1969
C. 1879
D. 1989.
-
A. Mumbai
B. London
C. Delhi
D. Australia .
-
A. Andhra Pradesh
B. Madhya pradesh
C. Uttar pradesh
D. Rajasthan .
-
A. Dr. Sarvepalli Radha Krishna
B. Sri.V.V.Giri
C. Smt. Prathiba Singh Patil
D. Dr. Babu Rajendra Prasad .
-
A. Smt. Meera kumari
B. Sri. Somnath Chaterjee
C. Om Birla
D. Sri.Neelam Sanjeeva Reddy
-
A. sri.K.G.Bala Krishnan
B. Sri. R.C. Lahoti
C. Sri.V.N. Khare
D. Ranjan Gogoi
-
A. 5th five year plan
B. 11th five year plan
C. 12th five year plan
D. 13th five year plan.
-
A. Chandighar
B. Kerala
C. Maharastra
D. West Bengal
-
A. 15 August 1947
B. 26 January 1950
C. 15 August 1958
D. 15 August 1959.
-
A. Caspian lake
B. Kolleru lake
C. Chilka lake
D. Victoria lake.
-
A. Sumatra
B. Green land
C. Madagaskar
D. Borneo.
-
A. 12
B. 22
C. 16
D. 20.
-
A. Sri Jai Ram Ramesh
B. Sri Prabha sridevan
C. Sri. A. N. Tewari
D. Sri Lokeswar Singh Panta.
-
A. Anantapur
B. Chittoor
C. Cuddapah
D. East Godavari
-
A. Vijay Kumar Bist
B. Sanjay Karol
C. Sunil Gaur
D. Ajay Kumar Mittal
-
A. Vijayawada
B. Eluru
C. Machilipatnam
D. Gudivada
-
A. Delhi
B. Pune
C. Mumbai
D. Chennai.
-
A. Sri Suresh Reddy
B. Sri Sripada rao
C. sri Ayya Devara Kaleswara Rao
D. Smt. Prathiba Bharati.
-
A. Sri Ranganath Mishra
B. Sri Narasimhan
C. Justice Radhakrishnan sworn
D. Sri. Nissar Ahmad Khukru.
-
A. Mrs. Lata Mangeskar
B. Dr. Mangalam Palli Bala Murali Krishna
C. Sri. Hari Prasad Charasia
D. Shoba Raj .
-
A. Osmania University
B. India Gandhi National Unversity
C. Jawahar Lal Nehru University
D. Kakateya University
-
A. 1936
B. 1937
C. 1938
D. 1939
-
A. Hegue
B. Washington D.C
C. Rome
D. Geneva
-
A. First
B. second
C. Third
D. Fourth
-
A. Tiger
B. Elephant
C. Wild buffalo
D. Horse
-
A. Andhra Pradesh
B. Madhya Pradesh
C. Maharastra
D. Bihar
-
A. Sarkaria
B. Mandal
C. M. N. Poonchi
D. None of these.
-
A. 2009 November 21
B. 2009 January 26
C. 2009 August 15
D. 2009 October 2.
-
A. Chicago
B. Rio-de-Janeiro
C. Madrid
D. Tokyo .
-
A. Abala
B. Kranti
C. Sabala
D. None of these
-
A. Sri Ahmadi
B. K.G. Bala Krishnan
C. H. L. Dattu
D. None of these
-
A. Crocodile
B. Dolphin
C. Deer
D. None of these
-
A. Sri. Ranga Rajan
B. Dr. Vijaya Kelkhar
C. Sri. K.C. Panth
D. Sri Neyogi
-
A. August 15
B. June 5
C. July 20
D. December 10.
-
A. Kalpana chawla
B. Arundhati roy
C. Sucheta kriplani
D. None of these.
-
A. January 2009
B. March 2009
C. February 2009
D. December 2009
-
A. New Delhi
B. Tokyo
C. Beijing
D. Kuala Lumpur
-
A. Haematology
B. Cytology
C. Histology
D. Bacteriology
-
A. QOMK
B. ACEF
C. ZXUT
D. UVWX
-
A. 78
B. 64
C. 66
D. 68
-
A.PK
B.LK
C.KL
D.PL
-
A. 38
B. 56
C. 42
D. 45
-
A. High-Up
B. Past-Present
C. Often-Seldom
D. Fresh-Stale
-
A. AEIM
B. BFJN
C. CGKO
D. FDKN
-
A.636
B.749
C.864
D.989
-
A.Daman and Diu
B.Puducherry
C.Delhi
D.Chennai
-
A. Daughter
B. Sister
C. Sister-in-law
D. Niece
-
A. Thursday
B. Friday
C. Sunday
D. Monday
-
A. rptr
B. rrtp
C. ptrr
D. tprt
-
A. EY
B. DZ
C. CY
D. CZ
-
A. Glass
B. Asphalt
C. Petrol
D. Wax
-
A.24
B.27
C.26
D.36
-
A. 4
B. 3
C. 5
D. 6
-
A. Saturn
B. Earth
C. Pluto
D. Mercury
-
A. K-11, M-13
B. L-12, M-14
C. L-12, N-14
D. K-12, M-14
-
A. iv, ii, i, iii
B. iii, iv, ii, i
C. iv, iii, i, ii
D. i, ii, iv, iii
-
A.Wednesday
B.Thursday
C.Tuesday
D.Monday
-
A.TUBOEQZE
B.CZQETUBO
C.TUBOCZQC
D.TUBOEBSE
-
A. RADON
B. RATION
C. NATIONAL
D. TRAIN
-
A. white
B. red
C. green
D. yellow
-
A. 5
B. 8
C. 13
D. 6
-
A. 150
B. 171
C. 230
D. 234
-
A. Grandfather
B. Uncle
C. Husband
D. Son
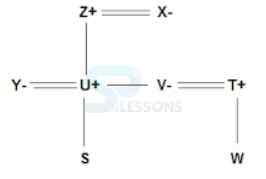
 77. How many male members are there in the family?
77. How many male members are there in the family?
-
A.Five
B.Three
C.Four
D.Cannot be determined
-
A. T is son of Z
B. V is daughter of X
C. Z has two sons
D. X has 2 grandsons
-
A. UV
B. SW
C. VT
D. XY
-
A.Mother
B.Sister
C.Aunt
D.Grandmother
-
A. 16 km
B. 25 km
C. 4 km
D. 0 km
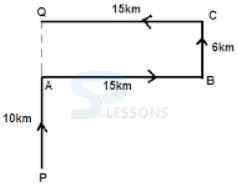
 82. Towards which direction was the vehicle moving before it stopped at point Q?
82. Towards which direction was the vehicle moving before it stopped at point Q?
-
A. North
B. East
C. South
D. West
-
A.QTS
B.UPT
C.URP
D.Data inadequate
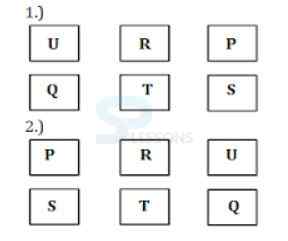
 84. Whose seat is between Q and S?
84. Whose seat is between Q and S?
-
A. T
B. U
C. R
D. P
-
A. P
B. Q
C. R
D. T

-
A. 16
B. 22
C. 28
D. 32
-
A.
 B.
B.  C.
C.  D.
D. 
-
A.
 B.
B.  C.
C. D.
D. E.
E.-
A.
 B.
B.  C.
C.  D.
D. 

-
A.
 B.
B. C.
C. D.
D.

-
A.
 B.
B. C.
C. D.
D.

-
A.
 B.
B.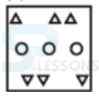 C.
C.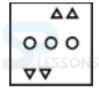 D.
D.
-
A. Q
B. R
C. T
D. W
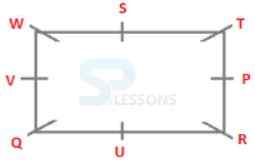
 94. How many persons sit between P and W when counted in the anti-clockwise direction from P?
94. How many persons sit between P and W when counted in the anti-clockwise direction from P?
-
A. None
B. One
C. Two
D. Three
-
A. S
B. U
C. P
D. T
-
A. Third to the left
B. Immediate to the right
C. Second to the right
D. Immediate to the left
-
A.UT
B.WR
C.US
D.SQ
-
A. If only conclusion I follows
B. If only conclusion II follows
C. If either conclusion I or II follows
D. If neither conclusion I nor II follow
 From the Venn diagram we can infer that conclusion I am definitely false. And as all mobile is a laptop and some mobile is watched we can say that some watches are laptop is true.
99. Statements:
No gentleman is poor.
All gentlemen are rich.
Conclusions:
I. No poor man is rich.
II. No rich man is poor.
Answer: Option D
Explanation:
From the Venn diagram we can infer that conclusion I am definitely false. And as all mobile is a laptop and some mobile is watched we can say that some watches are laptop is true.
99. Statements:
No gentleman is poor.
All gentlemen are rich.
Conclusions:
I. No poor man is rich.
II. No rich man is poor.
Answer: Option D
Explanation:
 From the Venn diagram we can see that both the conclusions I and II are not true for all the cases. Hence both I and II do not follow.
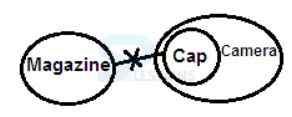
100. Statements:
No magazine is cap.
All caps are cameras.
Conclusions:
I. No camera is magazine.
II. Some cameras are magazines.
Answer: Option C
Explanation:
From the Venn diagram we can see that both the conclusions I and II are not true for all the cases. Hence both I and II do not follow.
100. Statements:
No magazine is cap.
All caps are cameras.
Conclusions:
I. No camera is magazine.
II. Some cameras are magazines.
Answer: Option C
Explanation:
 From the Venn diagram we can see that after considering all the cases either conclusion I or II will be true.
From the Venn diagram we can see that after considering all the cases either conclusion I or II will be true.
1. The additive inverse of rational number [latex]\frac{3}{4}[/latex]?
51. What is the ratio of the total number of men in the city C to the total number of women in the city E?
-
A. [latex]\frac{4}{3}[/latex]
B. [latex]\frac{-4}{3}[/latex]
C. [latex]\frac{-3}{4}[/latex]
D. 0
-
A. 2 and 4
B. 2 and 6
C. 2 and 3
D. 4 and 6
-
A. 0
B. 1
C. 2
D. Infinity
-
A. degree
B. radiant
C. cms
D. geometric measure
-
A. 2x%
B. ([latex]\frac{10}{x+x²}[/latex])%
C. ([[latex]\frac{2x + x²}{100}[/latex])%
D. ([latex]\frac{x + x²}{100}[/latex])%
-
A. 4
B. 5
C. 6
D. 10
-
A. 26%
B. 25%
C. 1%
D. 4%
-
A. Rs. 218 ([latex]\frac{13}{187}[/latex])
B. Rs. 207 ([latex]\frac{13}{17}[/latex])
C. Rs. 225 ([latex]\frac{13}{1 7}[/latex])
D. Rs. 211 ([latex]\frac{13}{17}[/latex])
-
A. 1% loss
B. 1% gain
C. 1.5% loss
D. 1.5% gain
-
A. 3
B. 6
C. 27
D. 144
-
A. 30
B. 60
C. 72
D. 90
-
A. 8, 12 and 16
B. 16, 24 and 32
C. 12, 18 and 24
D. None of the above
-
A. 144 , 96,64
B. 162 , 108,72
C. 180 , 120 , 80
D. 189,126,84
-
A. 8
B. 10
C. 12
D. 14
-
A. 27 km/hr
B. 26 km/hr
C. 25 km/hr
D. 24 km/hr
-
A. 30
B. 75
C. 35
D. 60
-
A. 13
B. 12
C. 6
D. 5
-
A. 1
B. 2
C. 3
D. 0
-
A. 900 km
B. 945 km
C. 990 km
D. 1350 km
-
A. 560 km
B. 506 km
C. 560 m
D. 650 m
-
A. 60
B. 80
C. 400
D. 40
-
A. Rs 50
B. Rs 75
C. Rs.100
D. Rs.150
-
A. x=15,y=18, and z=21
B. x=15,y=21, and z=21
C. x=18,y=18, and z=21
D. x=15,y=18, and z=15
-
A. 6 hours
B. 8 hours
C. 10 hours
D. 12 hours
-
A. 80 days
B. 50 days
C. 25 days
D. 12 days
-
A. 21%
B. 43%
C. 25%
D. 12%
-
A. 8000
B. 7200
C. 9000
D. 8800
-
A. 2, 27, 500
B. 1, 12, 000
C. 1, 17, 000
D. 1, 12, 250
-
A. 3 hours 15 min
B. 3 hours 45 min
C. 3 hours 40 min
D. 3 hours 50 min
-
A. 28 hours
B. 25 hours
C. 21 hours
D. 20 hours
-
A. Rs. 20000
B. Rs. 5000
C. Rs. 10000
D. Rs. 15000
-
A. Rs. 100
B. Rs. 105
C. Rs. 50
D. Rs. 110
-
A. Rs. 1,050
B. Rs. 417.50
C. Rs. 435
D. Rs. 1,000
-
A. Rs. 350
C. Rs. 375
C. Rs. 360
D. Rs. 400
-
A. No Loss / No Gain
B.5% Loss
C. 1% Gain
D. 1% Loss
-
A. 240π cu.cm
B. 5280 cu.cm
C. 620π cu.cm
D. 360π cu.cm
-
A. [latex]\frac{1}{9}[/latex]
B. [latex]\frac{2}{9}[/latex]
C. [latex]\frac{7}{9}[/latex]
D. [latex]\frac{8}{9}[/latex]
-
A. 4400 cm³
B. 15400 cm³
C. 35000 cm³
D. 144 cm³
-
A. 11385 m²
B. 10395 m²
C. 9900 m²
D. 990 m²
-
A. 46.2 kg
B. 24.2 kg
C. 26.4 kg
D. 18.6 kg
-
A. 512
B. 984
C. 1024
D. 1032
-
A. 3 × 10[latex]^{-5}[/latex]
B. 3 × 10[latex]^{4}[/latex]
C. 3 × 10[latex]^{5}[/latex]
D. 30
-
A. 10
B. 100
C. 1000
D. 10000
-
A. 4
B. 7
C. 8
D. 16
-
A. 7 × 8 8[latex]^{-25}[/latex]
B. 7 × 8 8[latex]^{-26}[/latex]
C. 8 × 8 8[latex]^{-26}[/latex]
D. 8 × 8 8[latex]^{-25}[/latex]
-
A. 0
B. [latex]\frac{1}{√2}[/latex]
C. [latex]\frac{1}{2}[/latex]
D. 1
-
A. 8
B. 10
C. 1
D. 2
-
A. 1
B. 0
C. 2 cos θ
D. 2 sin θ
-
A. [latex]\frac{4}{5}[/latex]
B. 1
C. [latex]\frac{1}{2}[/latex]
D. [latex]\frac{1}{√3}[/latex]
-
A. √3
B. 1
C. [latex]\frac{1}{2}[/latex]
D. [latex]\frac{1}{√3}[/latex]
| City | Total populations | Percentage of men | Percentage of women | Percentage of children |
|---|---|---|---|---|
| A | 4860 | 45% | 35% | 20% |
| B | 4540 | 35% | 55% | 10% |
| C | 1500 | 44% | 38% | 18% |
| D | 4850 | 38% | 48% | 14% |
| E | 3650 | 56% | 36% | 8% |
-
A. 11 : 9
B. 110 : 221
C. 110 : 217
D. 110 : 219
-
A. 984
B. 948
C. 931
D. 924
-
A. 453
B. 395
C. 473
D. 415
-
A. 106%
B. 102%
C. 110%
D. 114%
-
A. 15873
B. 19458
C. 15993
D. 16733
-
A. Electricity
B. Coal
C. Sun
D. Wood and animal dung
-
A. Were originally formed in marine environment
B. Contain carbon
C. Have undergone the same set of geological processes during their formation
D. Represent the remains of one living organisms
-
A. Liquefaction
B. Carbonation
C. Catalytic conversion
D. Cracking
-
A. Nuclear fuel
B. Coal
C. Natural gas
D. Bio gas
-
A. Colour less
B. Odorless
C. Smelly yellow to black liquid
D. Odorless yellow to black liquid
-
A. Volume
B. Area
C. Heat content
D. Temperature
-
A. 1920
B. 1928
C. 1925
D. 1938
-
A. Nuclear reactor
B. Solar reactor
C. OTEC
D. Bio-gas reactor
-
A. Stomach
B. Food Pipe
C. Mouth
D. Small Intestine
-
A. Penicillium
B. Plasmodium
C. Paramecium
D. Parrot
-
A. Pepsin
B. Trypsin
C. Amylase
D. None of the above
-
A. PDP
B. DTP
C. ATP
D. ADP
-
A. Lenticels
B. Stomata
C. Root hair
D. Air tubes
-
A. Pigeon
B. Lizard
C. Fish
D. Lion
-
A. Birds reptiles and insects
B. Frogs and toads
C. Mammals and birds
D. Fishes and fresh water protozoans
-
A. Excrete large amount of water
B. Actively pump salts through skin
C. Excrete large amount of salts in urine
D. Conserve water
-
A. Aminotelism
B. Ureotelism
C. Uricotelism
D. Ammonotelism
-
A. Septal nephridia
B. Macronephric nephridia
C. Pharyngeal nephridia
D. Integumentary nephridia
-
A. Urea
B. Uric acid and urea
C. Uric acid
D. Ammonia and uric acid
-
A. Vegetative reproduction
B. Asexual reproduction
C. Sexual reproduction
D. Budding
-
A. Double fertilization
B. Self pollination
C. Cross fertilization
D. No fertilization
-
A. Tallness is the dominant trait
B. Shortness is the dominant trait
C. Tallness is the recessive trait
D. Height of pea plant is not governed by gene 'T' or 't'
-
A. For every hormone there is a gene
B. For every protein there is a gene
C. For production of every enzyme there is a gene
D. For every molecule of fat there is a gene
-
A. Round and yellow
B. Round and green
C. Wrinkled and green
D. Wrinkled and yellow
-
A. ethane and propane
B. propane and butane
C. ethane and ethane
D. butane and 2-methyl propane
-
A. Alkaline KMnO4
B. Conc. H2SO4
C. Acidified K2Cr2O7
D. All of above
-
A. ethanol only
B. ethanol and methanol (50%)
C. ethanol and methanol (5%)
D. methanol only
-
A. Isobutane
B. Ter-butyl alcohol
C. Secondary-propyl alcohol
D. All of above
-
A. Sodium nitrate
B. calcium hydrogen carbonate
C. calcium carbonate
D. magnesium carbonate
-
A. isoprene
B. glycerol
C. butane
D. ethylene glycol
-
A. The solid shell of inorganic materials on the surface of the Earth
B. The thin shell of organic matter on the surface of earth comprising of all the living things
C. The sphere which occupies the maximum volume of all the spheres
D. All of the above
-
A. Atmosphere
B. Lithosphere
C. Hydrosphere
D. Biosphere
-
A. Air pollution
B. Soil pollution
C. Soil erosion
D. Water pollution
-
A. Troposphere
B. Mesosphere
C. Ionosphere
D. Thermosphere
-
A. Entire atmosphere consisting of troposphere, stratosphere, mesosphere, and thermosphere
B. Entire hydrosphere-representing the entire collection of water over the Earth as well as inside the Earth
C. A small zone of Earth, where the lithosphere, hydrosphere, and atmosphere come in contact with one another
D. Entire lithosphere-representing the solid Earth and its interior
-
A. Cosmic year
B. Astronomical year
C. Light year
D. Parsec
-
A. Cosmology
B. Cosmography
C. Astronomy
D. None of these
-
A. Moon and earth have gravitational force
B. Moon cannot change its position
C. The period of rotation of the moon on its axis and period of revolution around the earth is almost the same
D. None of these
-
A. Size
B. Rotational speed
C. Mass
D. Density
-
A. Because earth rotates about its axis
B. Because earth revolves around the sun
C. Because of optical illusion
D. Because celestial bodies are changing their position
-
A. Displace large number of peasants and trebles without proper rehabilitation
B. Swallow up huge amounts of public money without the generation of proportionate benefits
C. Contribute enormously to deforestation and the loss of biological diversity
D. all of the above.
-
A. People who live in or around the forest
B. The industrial
C. The wildlife and native enthusiasts
D. The forest department of the government.
-
A. Government of India.
B. Botanical Survey of India
C. UNESCO
D. UNDP.
-
A. Conservation of natural resources
B. Development of new breeds of forest plants
C. Zoological survey of India
D. Forest conservation.
-
A. Potential energy
B. Kinetic energy
C. Both A and B of these
D. None of these.





