1. Arithmetic
2. Algebra
3. Trigonometry
4. Geometry
5. Mensuration
6. Statistics
1. Arithmetic Related Topics
Natural numbers:
1. Which one of the following is not a prime number?
Answer: Option D
Explanation:
91 is divisible by 7. So, it is not a prime number.
2. How many of the following numbers are divisible by 132 ?
264, 396, 462, 792, 968, 2178, 5184, 6336
Answer: Option A
Explanation:
132 = 4 x 3 x 11
So, if the number divisible by all the three number 4, 3 and 11, then the number is divisible by 132 also.
264--> 11,3,4 (/)
396 --> 11,3,4 (/)
462 --> 11,3 (X)
792 --> 11,3,4 (/)
968 --> 11,4 (X)
2178 --> 11,3 (X)
5184 --> 3,4 (X)
6336 --> 11,3,4 (/)
Therefore the following numbers are divisible by 132 : 264, 396, 792 and 6336.
Required number of number = 4.
Decimal Fractions:
1. What decimal of an hour is a second ?
A. .0025
B. .0256
C. .00027
D. .000126
Answer: Option C
Explanation:
Required decimal = [latex]\frac{1}{60*60}[/latex]
= [latex]\frac{1}{3600}[/latex]
= .00027
2. [latex]\frac{.009}{?}[/latex]= .01
A. .0009
B. .09
C. .9
D. 9
Answer: Option C
Explanation:
Let [latex]\frac{.009}{x}[/latex] = .01
Then x =[latex]\frac{.009}{.01}[/latex] = .9
Percentages:
1. A batsman scored 110 runs which included 3 boundaries and 8 sixes. What percent of his total score did he make by running between the wickets?
A. 45%
B. 45[latex]\frac{5}{11}[/latex] %
C. 54[latex]\frac{6}{11}[/latex] %
D. 55%
Answer: Option B
Explanation:
Number of runs made by running = 110 - (3 x 4 + 8 x 6)
= 110 - (60)
= 50.
Required percentage =([latex]\frac{50}{110}[/latex] * 100) = 45[latex]\frac{5}{11}[/latex] %
2. Two students appeared at an examination. One of them secured 9 marks more than the other and his marks were 56% of the sum of their marks. The marks obtained by them are:
A. 39, 30
B. 41, 32
C. 42, 33
D. 43, 34
Answer: Option C
Explanation:
Let their marks be (x + 9) and x.
Then, x + 9 =[latex]\frac{56}{100}[/latex](x + 9 + x)
25(x + 9) = 14(2x + 9)
3x = 99
x = 33
So, their marks are 42 and 33.
Profit & Loss:
1. Alfred buys an old scooter for Rs. 4700 and spends Rs. 800 on its repairs. If he sells the scooter for Rs. 5800, his gain percent is:
A. 4[latex]\frac{4}{7}[/latex]%
B. 5[latex]\frac{5}{11}[/latex]%
C. 10%
D. 12%
Answer: Option B
Explanation:
Cost Price (C.P.) = Rs. (4700 + 800) = Rs. 5500.
Selling Price (S.P.) = Rs. 5800.
Gain = (S.P.) - (C.P.) = Rs.(5800 - 5500) = Rs. 300.
Gain % =([latex]\frac{300}{5500}[/latex] * 100) % = 5[latex]\frac{5}{11}[/latex]%
2. The cost price of 20 articles is the same as the selling price of x articles. If the profit is 25%, then the value of x is:
Answer: Option B
Explanation:
Let C.P. of each article be Re. 1 C.P. of x articles = Rs. x.
S.P. of x articles = Rs. 20.
Profit = Rs. (20 - x).
([latex]\frac{20-x}{x}[/latex] * 100 = 25)
2000 - 100x = 25x
125x = 2000
x = 16.
Ratio & Proportion:
1. The ratio of the number of boys and girls in a college is 7 : 8. If the percentage increase in the number of boys and girls be 20% and 10% respectively, what will be the new ratio?
A. 8 : 9
B. 17 : 18
C. 21 : 22
D. Cannot be determined
Answer: Option C
Explanation:
Originally, let the number of boys and girls in the college be 7x and 8x respectively.
Their increased number is (120% of 7x) and (110% of 8x).
= ([latex]\frac{120}{100}[/latex]*7x) and ([latex]\frac{110}{100}[/latex]*8x)
= ([latex]\frac{42x}{5}[/latex]) and ([latex]\frac{44x}{5}[/latex])
The required ratio =([latex]\frac{42x}{5}[/latex]):([latex]\frac{44x}{5}[/latex]) = 21 : 22.
2. Salaries of Ravi and Sumit are in the ratio 2 : 3. If the salary of each is increased by Rs. 4000, the new ratio becomes 40 : 57. What is Sumit's salary?
A. Rs. 17,000
B. Rs. 20,000
C. Rs. 25,500
D. Rs. 38,000
Answer: Option D
Explanation:
Let the original salaries of Ravi and Sumit be Rs. 2x and Rs. 3x respectively.
Then,[latex]\frac{2x + 4000}{3x + 4000}[/latex] = [latex]\frac{40}{57}[/latex]
57(2x + 4000) = 40(3x + 4000)
6x = 68,000
3x = 34,000
Sumit's present salary = (3x + 4000) = Rs.(34000 + 4000) = Rs. 38,000.
2. Algebra Related Topics:
LCM & HCF:
1. Find the greatest number that will divide 43, 91 and 183 so as to leave the same remainder in each case.
Answer: Option A
Explanation:
Required number = H.C.F. of (91 - 43), (183 - 91) and (183 - 43)
= H.C.F. of 48, 92 and 140 = 4.
2. The H.C.F. of two numbers is 23 and the other two factors of their L.C.M. are 13 and 14. The larger of the two numbers is:
A. 276
B. 299
C. 322
D. 345
Answer: Option C
Explanation:
Clearly, the numbers are (23 x 13) and (23 x 14).
Larger number = (23 x 14) = 322.
Quadratic Equations
1. Find the roots of the quadratic equation: [latex]x^{2}[/latex]+ 2x - 15 = 0?
A. -5, 3
B. 3, 5
C. -3, 5
D. -3,-5
Answer: Option A
Explanation:
[latex]x^{2}[/latex]+ 5x - 3x - 15 = 0
x(x + 5) - 3(x + 5) = 0
(x - 3)(x + 5) = 0
=> x = 3 or x = -5.
2. Find the roots of the quadratic equation: [latex]2x^{2}[/latex]+ 3x - 9 = 0?
A. 3, -[latex]\frac{3}{2}[/latex]
B. [latex]\frac{3}{2}[/latex], -3
C. -[latex]\frac{3}{2}[/latex], -3
D. [latex]\frac{3}{2}[/latex], 3
Answer: Option B
Explanation:
[latex]2x^{2}[/latex] + 6x - 3x - 9 = 0
2x(x + 3) - 3(x + 3) = 0
(x + 3)(2x - 3) = 0
=> x = -3 or x = [latex]\frac{3}{2}[/latex].
Areas of squares:
1. The ratio between the length and the breadth of a rectangular park is 3 : 2. If a man cycling along the boundary of the park at the speed of 12 km/hr completes one round in 8 minutes, then the area of the park (in sq. m) is:
A. 15360
B. 153600
C. 30720
D. 307200
Answer: Option B
Explanation:
Perimeter = Distance covered in 8 min. =([latex]\frac{12000}{60}[/latex] * 8) =1600 m.
Let length = 3x metres and breadth = 2x metres.
Then, 2(3x + 2x) = 1600 or x = 160.
Length = 480 m and Breadth = 320 m.
Area = (480 x 320)[latex] m^{2}[/latex] = 153600 [latex] m^{2}[/latex].
2. An error 2% in excess is made while measuring the side of a square. The percentage of error in the calculated area of the square is:
A. 2%
B. 2.02%
C. 4%
D. 4.04%
Answer: Option D
Explanation:
100 cm is read as 102 cm.
A1 = (100 x 100)[latex] cm^{2}[/latex] and A2 (102 x 102) [latex] cm^{2}[/latex].
(A2 - A1) = [latex] (102)^{2}[/latex]) - ([latex] (100)^{2}[/latex]
= (102 + 100) x (102 - 100)
= 404 [latex] cm^{2}[/latex]
Percentage error =([latex]\frac{404}{100*100}[/latex] * 100) = 4.04%
Volume and Surface Area:
1. A boat having a length 3 m and breadth 2 m is floating on a lake. The boat sinks by 1 cm when a man gets on it. The mass of the man is:
A. 12 kg
B. 60 kg
C. 72 kg
D. 96 kg
Answer: Option B
Explanation:
Volume of water displaced = (3 x 2 x 0.01)[latex]m^{3}[/latex]
= 0.06 [latex]m^{3}[/latex].
Mass of man = Volume of water displaced x Density of water
= (0.06 x 1000) kg
= 60 kg.
2. 50 men took a dip in a water tank 40 m long and 20 m broad on a religious day. If the average displacement of water by a man is 4 [latex]m^{3}[/latex], then the rise in the water level in the tank will be:
A. 20 cm
B. 25 cm
C. 35 cm
D. 50 cm
Answer: Option B
Explanation:
Total volume of water displaced = (4 x 50) [latex]m^{3}[/latex]= 200 [latex]m^{3}[/latex].
Rise in water level =([latex]\frac{200}{40 x 20}[/latex])m 0.25 m = 25 cm
3. Trigonometry Related Topics
Simple trigonometric identities:
1. For Cosine Rule of any triangle ABC,[latex]b^{2}[/latex] is equal to
A. [latex]a^{2}[/latex] - [latex]c^{2}[/latex] 4bc cos A
B. [latex]a^{2}[/latex] + [latex]c^{2}[/latex] - 2ac cos B
C. [latex]a^{2}[/latex] -[latex]c^{2}[/latex] + 2ab cos A
D. [latex]a^{3}[/latex] + [latex]c^{3}[/latex] - 3ab cos A
Answer: Option B
Explanation:
a² + c² - 2ac cos B
2 . For Cosine Rule of any triangle ABC,[latex]c^{2}[/latex] is equal to
A. [latex]a^{2}[/latex] - [latex]b^{2}[/latex] + 2ab sin A
B. [latex]a^{2}[/latex] + [latex]b^{2}[/latex] + 2ab cos A
C. [latex]a^{2}[/latex] + [latex]b^{2}[/latex] - 2ab cos C
D. [latex]c^{2}[/latex] +[latex]a^{2}[/latex] + 2ac cos C
Answer: Option C
Explanation:
a² + b² - 2ab cos C
3 . In a triangle ABC, if angle A = 72° , angle B = 48° and c = 9 cm then Ĉ is
A. 60°
B. 63°
C. 66°
D. 69°
Answer: Option C
Explanation:
66°
heights and distances:
1. A man standing at a point P is watching the top of a tower, which makes an angle of elevation of 30° with the man's eye. The man walks some distance towards the tower to watch its top and the angle of the elevation becomes 60°. What is the distance between the base of the tower and the point P?
A. 43 units
B. 8 units
C. 12 units
D. Data inadequate
Answer: Option D
Explanation:
One of AB, AD and CD must have given.
So, the data is inadequate.
2. The angle of elevation of a ladder leaning against a wall is 60° and the foot of the ladder is 4.6 m away from the wall. The length of the ladder is:
A. 2.3 m
B. 4.6 m
C. 7.8 m
D. 9.2 m
Answer: Option D
Explanation:
Let AB be the wall and BC be the ladder.
[latex]\frac{AB}{BC}[/latex] = cos 60° =[latex]\frac{1}{2}[/latex]
BC = 2 x AC
= (2 x 4.6) m
= 9.2 m.
5. Mensuration
Volume and Surface Area:
1. In a shower, 5 cm of rain falls. The volume of water that falls on 1.5 hectares of ground is:
A. 75 cu. m
B. 750 cu. m
C. 7500 cu. m
D. 75000 cu. m
Answer: Option B
Explanation:
1 hectare = 10,000 [latex]m^{2}[/latex]
So, Area = (1.5 x 10000) [latex]m^{2}[/latex]= 15000 [latex]m^{2}[/latex].
Depth =[latex]\frac{5}{100}[/latex]m = [latex]\frac{1}{20}[/latex]m
Volume = (Area * Depth) =(15000[latex]\frac{1}{20}[/latex]) [latex]m^{3}[/latex]=750 [latex]m^{3}[/latex]
2. A hall is 15 m long and 12 m broad. If the sum of the areas of the floor and the ceiling is equal to the sum of the areas of four walls, the volume of the hall is:
A. 720
B. 900
C. 1200
D. 1800
Answer: Option C
Explanation:
2(15 + 12) * h = 2(15 * 12)
h= [latex]\frac{180}{27}[/latex]m= [latex]\frac{20}{3}[/latex]m
Volume = (15*12*[latex]\frac{20}{3}[/latex]) [latex]m^{3}[/latex]= 1200 [latex]m^{3}[/latex]
6. Statistics
Bar charts:
Study the bar chart and answer the question based on it.
1. What was the percentage decline in the production of fertilizers from 1997 to 1998?
A. 33(1/3)%
B. 20%
C. 25%
D. 21%
Answer: Option C
Explanation:
Required percentage =[latex]\frac{(45 - 60)}{60}[/latex]% = -25%
There is a decline of 25% in production from 1997 to 1998.
2. The average production of 1996 and 1997 was exactly equal to the average production of which of the following pairs of years?
A. 2000 and 2001
B. 1999 and 2000
C. 1998 and 2000
D. 1995 and 2001
Answer: Option D
Explanation:
Average production (in 10000 tonnes) of 1996 and 1997= [latex]\frac{(40+60)}{2}[/latex]= 50
We shall find the average production (in 10000 tonnes) for each of the given alternative pairs:
2000 and 2001 =[latex]\frac{50+75}{2}[/latex]= 62.5
1999 and 2000 =[latex]\frac{65+50}{2}[/latex]= 57.5
1998 and 2000 =[latex]\frac{45+50}{2}[/latex]= 47.5
1995 and 1999 =[latex]\frac{25+65}{2}[/latex]= 45
1995 and 2001 =[latex]\frac{25+75}{2}[/latex]= 50
The average production of 1996 and 1997 is equal to the average production of 1995 and 2001.
3. What was the percentage increase in production of fertilizers in 2002 compared to that in 1995?
A. 320%
B. 300%
C. 220%
D. 200%
Answer: Option C
Explanation:
Required percentage =[[latex]\frac{(80 - 25)}{25}[/latex] * 100] = 220%
Pie charts:
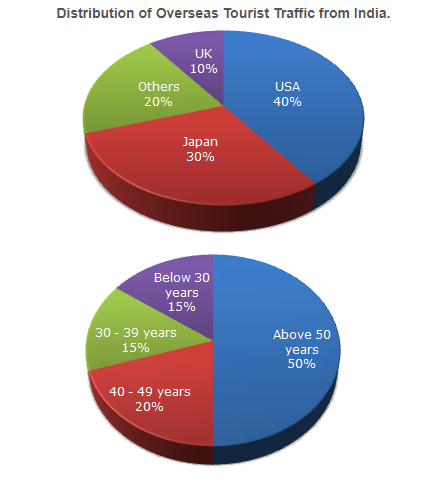
The following pie charts exhibit the distribution of the overseas tourist traffic from India. The two charts shows the tourist distribution by country and the age profiles of the tourists respectively.
1. What percentage of Indian tourist went to either USA or UK ?
A. 40 %
B. 50 %
C. 60 %
D. 70 %
Answer: Option B
Explanation:
(40+10) = 50% (from first chart)
2. The ratio of the number of Indian tourists that went to USA to the number of Indian tourists who were below 30 years of age is ?
A. 2:1
B. 8:3
C. 3:8
D. Cannot be determined
Answer: Option B
Explanation:
40:15 = 8:3
3. If amongst other countries, Switzerland accounted for 25% of the Indian tourist traffic, and it is known from official Swiss records that a total of 25 lakh Indian tourists had gone to Switzerland during the year, then find the number of 30-39 year old Indian tourists who went abroad in that year ?
A. 18.75 lakh
B. 25 lakh
C. 50 lakh
D. 75 lakh
Answer: Option D
Explanation:
Tourist traffic from other countries to Swiz is 20%.
Amongst this 20%, 25% of traffic from India.
So, 25% of 20% = 5% corresponds to the Indian traffic in Switzerland.
5 % corresponds to Switzerland's 25 lakh. Hence 15% will be 75 lakh.
Collection and tabulation of statistical data
The following table gives the percentage of marks obtained by seven students in six different subjects in an examination.
| Student |
Subject (Max. Marks) |
| Maths |
Chemistry |
Physics |
Geography |
History |
Computer Science |
| (150) |
(130) |
(120) |
(100) |
(60) |
(40) |
| Ayush |
90 |
50 |
90 |
60 |
70 |
80 |
| Aman |
100 |
80 |
80 |
40 |
80 |
70 |
| Sajal |
90 |
60 |
70 |
70 |
90 |
70 |
| Rohit |
80 |
65 |
80 |
80 |
60 |
60 |
| Muskan |
80 |
65 |
85 |
95 |
50 |
90 |
| Tanvi |
70 |
75 |
65 |
85 |
40 |
60 |
| Tarun |
65 |
35 |
50 |
77 |
80 |
80 |
1. What are the average marks obtained by all the seven students in Physics? (rounded off to two digit after decimal)
A. 77.26
B. 89.14
C. 91.37
D. 96.11
Answer: Option B
Explanation:
Average marks obtained in Physics by all the seven students
=[latex]\frac{1}{7}[/latex] * [ (90% of 120) + (80% of 120) + (70% of 120) + (80% of 120) + (85% of 120) + (65% of 120) + (50% of 120) ]
=[latex]\frac{1}{7}[/latex]*[ (90 + 80 + 70 + 80 + 85 + 65 + 50)% of 120 ]
=[latex]\frac{1}{7}[/latex]* [ 520% of 120 ]
=[latex]\frac{624}{7}[/latex]
= 89.14.
2. The number of students who obtained 60% and above marks in all subjects is?
Answer: Option B
Explanation:
From the table it is clear that Sajal and Rohit have 60% or more marks in each of the six subjects.
 Introduction
Introduction  Pattern
Pattern  Samples
Samples