Data Interpretation ( Tabular, Radar graph )

1. What is the different between the number of students passed with 30 as cut-off marks in Chemistry and those passed with 30 as cut-off marks in aggregate?

A. 3 B. 4 C. 5 D. 6

Answer: Option (D)
Explanation: Required difference = (No. of students scoring 30 and above marks in Chemistry) - (Number of students scoring 30 and above marks in aggregate) = 27 - 21 = 6.
2. If at least 60% of marks in Physics are required for pursuing higher studies in Physics, how many students will be eligible to pursue higher studies in Physics?

A. 27 B. 32 C. 34 D. 41

Answer: Option (B)
Explanation: We have 60% of 50 = ([latex]\frac{60}{100}[/latex] x 50 ) = 30. Therefore Required number = No. of students scoring 30 and above marks in Physics = 32
3. The percentage of the number of students getting at least 60% marks in Chemistry over those getting at least 40% marks in aggregate, is approximate?

A. 21% B. 27% C. 29% D. 31%

Answer: Option (C)
Explanation: Number of students getting at least 60% marks in Chemistry = Number of students getting 30 and above marks in Chemistry = 21. Number of students getting at least 40% marks in aggregate = Number of students getting 20 and above marks in aggregate = 73. Required percentage =([latex]\frac{21}{73}[/latex]x 100)% = 28.77% ≈ 29%.
4. The number of students scoring less than 40% marks in aggregate is?

A. 13 B. 19 C. 20 D. 27

Answer: Option (D)
Explanation: We have 40% of 50 = ([latex]\frac{40}{100}[/latex] x 50 ) = 20. Therefore Required number = Number of students scoring less than 20 marks in aggregate = 100 - Number of students scoring 20 and above marks in aggregate = 100 - 73 = 27.
5. If it is known that at least 23 students were eligible for a Symposium on Chemistry, then the minimum qualifying marks in Chemistry for eligibility to Symposium would lie in the range?

A. 40-45 B. 30-40 C. 20-30 D. Below 20

Answer: Option (C)
Explanation: Since 66 students get 20 and above marks in Chemistry and out of these 21 students get 30 and above marks, therefore to select top 35 students in Chemistry, the qualifying marks should lie in the range 20-30.
Bar Graph
Direction (1 - 3): Refer to the following graph of sales and profit figures of ABC Ltd and answer the questions that follow.

1. Return on sales (Profit/sales) was highest in which year?

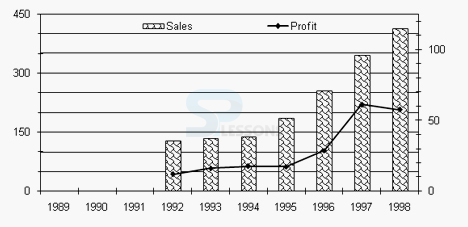
A. 1995 B. 1996 C. 1997 D. 1998

Answer: Option (C)
Explanation: Return on sales in 1995 = [latex]\frac{20}{180}[/latex] or 0.111 Return on sales in 1996 = [latex]\frac{30}{260}[/latex] or 0.115 Return on sales in 1997 = [latex]\frac{60}{345}[/latex]or 0.173 Return on sales in 1998 = [latex]\frac{55}{420}[/latex] or 0.130 So, highest return comes in 1997.
2. How many times return on sales (profit/sales) exceeded 15 % ?

A. Once B. Twice C. Thrice D. Never

Answer: Option (A)
Explanation: Return on sales in 1992 = [latex]\frac{12}{130}[/latex] or 0.09 Return on sales in 1993 = [latex]\frac{18}{135}[/latex] or 0.13 Return on sales in 1994 = [latex]\frac{19}{140}[/latex] or 0.13 Return on sales in 1995 = [latex]\frac{20}{180}[/latex] or 0.111 Return on sales in 1996 = [latex]\frac{30}{260}[/latex] or 0.115 Return on sales in 1997 = [latex]\frac{60}{345}[/latex] or 0.173 Return on sales in 1998 = [latex]\frac{55}{420}[/latex] or 0.130 Return on sales exceeds 15% only in 1997.
3. How many times growth in profit over the previous year exceeded 50% was registered?

A. Once B. Twice C. Thrice D. Never

Answer: Option (B)
Explanation: Profit growth exceeds 50% in 1996 i.e. from 18 to 30 and in 1997 from 30 to 60. This is not happening in any other year. Therefore the answer is twice.
Direction (4 - 5): Refer to the following graph of sales and profit figures of ABC Ltd and answer the questions that follow.

4. The highest average annual growth rate in revenue is

A. 270% B. 154% C. 108% D. 54%

Answer: Option (D)
Explanation: By observation, we can see that there is no growth from 1995-96 to 1996-97. From 1996-97 to 2001-02, the maximum growth is clearly visible from the graph i.e. 1000 to 3700. So, for the five years growth is about 270%. Finally, the average annual growth would be ([latex]\frac{270}{5}[/latex])= 54%.
5. Profitability (Profit / Sales) is the highest in

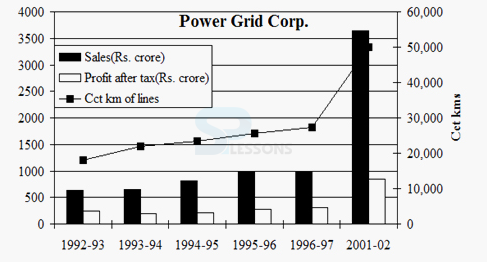
A. 1992-93 B. 1993-94 C. 2001-02 D. 1996-97

Answer: Option (A)
Explanation: Profit/Sales for 1992-93 = 300/600 = 0.50 For 1993-94 = [latex]\frac{200}{700}[/latex] = 0.29. For 2001-02 =[latex]\frac{750}{3700}[/latex]=0.20. For 1996-97 = [latex]\frac{350}{1000}[/latex]= 0.35. So, the profitability for 1992-93 is the highest.
Number Series
1. Look at this series: F2, __, D8, C16, B32, ... What number should fill the blank?

A. A16 B. G4 C. E4 D. E3

Answer: Option (C)
Explanation: The letters decrease by 1; the numbers are multiplied by 2.
2. Look at this series: 664, 332, 340, 170, ____, 89, ... What number should fill the blank?

A. 85 B. 97 C. 109 D. 178

Answer: Option (D)
Explanation: This is an alternating division and addition series: First, divide by 2, and then add 8.
3. Look at this series: V, VIII, XI, XIV, __, XX, ... What number should fill the blank?

A. IX B. XXIII C. XV D. XVII

Answer: Option (D)
Explanation: This is a simple addition series; each number is 3 more than the previous number.
4. Look at this series: 70, 71, 76, __, 81, 86, 70, 91, ... What number should fill the blank?

A. 70 B. 71 C. 80 D. 96

Answer: Option (A)
Explanation: In this series, 5 is added to the previous number; the number 70 is inserted as every third number.
5. Look at this series: 8, 43, 11, 41, __, 39, 17, ... What number should fill in the blank?

A. 8 B. 14 C. 43 D. 44

Answer: Option (B)
Explanation: This is a simple alternating addition and subtraction series. The first series begins with 8 and adds 3; the second begins with 43 and subtracts 2.

Data Sufficiency
1. A can do a piece of work in 4 hours; B and C together can do it in 3 hours, while A and C together can do it in 2 hours. How long will B alone take to do it?

A. 8 hours B. 10 hours C. 12 hours D. 24 hours

Answer: Option (C)
Explanation: A's 1 hour's work = [latex]\frac{1}{4}[/latex]; (B + C)'s 1 hour's work =[latex]\frac{1}{3}[/latex]; (A + C)'s 1 hour's work =[latex]\frac{1}{2}[/latex]. (A + B + C)'s 1 hour's work = ([latex]\frac{1}{4}[/latex] + [latex]\frac{1}{3}[/latex])=[latex]\frac{7}{12}[/latex]. B's 1 hour's work =([latex]\frac{7}{12}[/latex]- [latex]\frac{1}{2}[/latex]) = [latex]\frac{1}{12}[/latex]. Therefore B alone will take 12 hours to do the work.
2. How long does a train 110 m long traveling at 60 kmph takes to cross a bridge of 170 m in length?

A. 1.68 sec B. 15 sec C. 16 sec D. 16.8 sec

Answer: Option (D)
Explanation: D = 110 + 170 = 280 m S = 60 * [latex]\frac{5}{18}[/latex] = [latex]\frac{50}{3}[/latex] T = 280 * [latex]\frac{3}{50}[/latex] = 16.8 sec
3. How much time will a train of length 200 m moving at a speed of 72 kmph take to cross another train of length 300 m, moving at 36 kmph in the same direction?

A. 50 sec B. 25 sec C. 40 sec D. 65 sec

Answer: Option (A)
Explanation: The distance to be covered = Sum of their lengths = 200 + 300 = 500 m. Relative speed = 72 -36 = 36 kmph = 36 * [latex]\frac{5}{18}[/latex] = 10 mps. Time required = d/s = [latex]\frac{500}{10}[/latex] = 50 sec.
4. I bought two books; for Rs.480. I sold one at a loss of 15% and others at a gain of 19% and then I found each book was sold at the same price. Find the cost of the book sold at a loss?

A. Rs.28 B. Rs.280 C. Rs.140 D. Rs.70

Answer: Option (B)
Explanation: x*([latex]\frac{85}{100}[/latex]) = (480 - x)[latex]\frac{119}{100}[/latex] x = 280
5. By selling an article at Rs.600, a profit of 25% is made. Find its cost price?

A. Rs.350 B. Rs.400 C. Rs.573 D. Rs.480

Answer: Option (D)
Explanation: SP = 600 CP = (SP)* ([latex]\frac{100}{(100+P)}[/latex]) = 600 * ([latex] \frac{100}{(100+25)}[/latex]) = 600 * ([latex] \frac{100}{125}[/latex]) = Rs.480