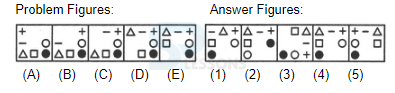
Prepositions
1. I have a distate -------- publicity.

A. about B. at C. against D. for

Answer: Option D
2. A steady mind triumphs ------ difficulties.

A. in B. over C. with D. at

Answer: Option B
Active Voice and Passive Voice
1. The French surrendered Quebec to the English in 1759.

A. Quebec was surrendered by the French to the English in 1759. B. Quebec was surrendered to the English in 1759 by the French. C. Quebec was surrendered in 1759 by the French to the English. D. The English were surrendered Quebec in 1759 by the French.

Answer: Option A
2. My uncle promised me a present.

A. I was promised by my undo a present. B. A present was promised by my uncle to me. C. I was promised a present by my uncle. D. I had been promised a present by my uncle.

Answer: Option C
Joining Sentences
1. You wish to succeed in life. You must work hard. (A) Unless you work hard ..... (B) In order to succeed in life ..... (C) Although you have to succeed .....

A. Only B B. A and C C. A and B D. Only A E. None of these

Answer: Option A
Explanation: The condition for being successful in life is to work hard, this is conveyed by B.
2. Childhood obesity is an alarming health issue. It is rife in the cities. (A) Childhood obesity is an alarming health issue that is ..... (B) Childhood obesity which is alarming ..... (C) Childhood obesity is an alarming health issue because of of.....

A. A and C B. B and C C. A and B D. Only A E. All the three

Answer: Option C
Explanation: The second sentence gives additional information to what is stated in the first. Hence the use of 'that' and 'which' can combine them without changing their meaning. But the use of 'because' distorts the meaning and hence cannot be used.
Spotting Errors
1. The war of Mahabharata (a) / is the full length illustration (b) / of a righteous war (c) / No error (d)

A. the war of Mahabharata B. is the full length illustration C. of a righteous war D. no error

Answer: Option A
2. It being rainy day (a) / we decided not to go out (b) / but to stay at home (c) / and watch a movie (d) / No error (e)

A. it is a rainy day B. we decided not to go out C. but to stay at home D. and watch a movie E. no error

Answer: Option A
Synonyms
1. Reel

A. Whirl B. Fish C. Hit D. Mistake

Answer: Option A
Explanation: one meaning of reel is to move around and round or to whirl
2. Inscrutable

A. Difficult B. Mysterious C. Inflexible D. Wary

Answer: Option B
Explanation: inscrutable means not easily interpreted or understood, or mysterious
Sentence Improvement
1. I could not help to laugh at the joke.

A. help to laugh at B. laugh at C. to laughing at D. none

Answer: Option A
2. She is tallest of all the girls.

A. a taller B. taller C. the taller D. the tallest

Answer: Option D
Error Correction (Phrase in colour)
1. Denizens of the Madras Zoo, on October 15, joined in the country-wide celebrations of the Wild-Life-Week, when some of them were taking out in a six-mile long procession through the prominent through fares of the city.

A. were taken out in B. are taken out on C. was taken out on D. ware taken out on E. No correction required

Answer: Option D
Explanation: The subject is 'some of them' which is plural. Hence 'were' should replace 'was'. Also, the second part of the sentence has to be in the passive as the animals cannot go out by themselves. They have to be taken out. Hence it has to be'were taken out'. They went 'on a procession'. The use of the preposition 'in' is inapt here. The correction, therefore, is 'were taken out on'.
2. It might be located right in the capital's posh area but the moment you step into this famous restaurant, cozy and warm enfolding you.

A. cozy and warm enfolds you B. cozy and warmth enfolds you C. coziness and warmth enfolds you D. coziness and warmth is enfolding you E. No correction required

Answer: Option C
Explanation: The last part is the main clause of the second sentence 'the moment you'. Hence it needs a finite verb. The sentence needs a verb in the present tense. Hence 'enfolds' should replace 'enfolding'. Also 'cozy and warm' is the subject which has to be given in the noun form. The correction is 'coziness and warmth enfolds you'.
Para Completion
1. Modern western cultures have encouraged the view that 'being human means to be creative' - not simply living in response to nature. ----- The geographic location of facilities, academic preparation, cultural stimulus, and sponsorship by preparation foundations and governments is mainly concentrated in advanced countries (A) But the opportunities to be imaginative and creative in the economic arena are not spread evenly around the world. (B) The present concentration in a few countries challenges the acceptability of globalization. (C) In economics and business, creativity for a nation means to be involved in scientific discovery and Technological Innovation.

A. A and B B. Only B C. Only A D. B and C E. A and C

Answer: Option C
Explanation: The first statement states that modern western cultures encourage creativity. Statement A which states that the opportunities to be imaginative and creative are not spread evenly across the world, ideally follows the first statement. The last statement which gives the reason for the unequal distribution of opportunities across the world ideally follows statement A.
2. Psychologists suggest that understanding or resolving a joke is a mental exercise - an act of creativity. ---- Psychologists use this aspect to assess the mental health of the elderly. (A) It involves playing with several alternative ideas and changing the mental perspective. (B) Pleasant relief comes when resolution occurs. (C) As we get senile, this ability to resolve comes down.

A. A and B B. B and C C. A and C D. All the three E. None of these

Answer: Option D
Explanation: The first sentence states the suggestion given by the psychologists regarding the understanding of a joke. The last sentence says that they use 'this aspect' to assess something and this aspect is 'the ability to resolve'. Hence C precedes the last sentence and B precedes C as the idea of 'resolution' is given in this sentence. Sentence A is a logical continuation of the opening sentence and hence the given sentence along with all the three sentences forms a coherent paragraph.
Sentence Completion
1. For nations conscious of the ----------- of modern war, peace must be the goal of their foreign policies.

A. incidence B. perils C. potentialities D. redundancies

Answer: Option C
2. A son who is unable to look his father in the face is

A. guilty B. arrogant C. timid D. ashamed

Answer: Option C
Fill in the blanks
1. A person who remains courageous even during times of _____ will ultimately emerge successfully. (A) grief (B) adversity (C) destruction (D) horror (E) suffering (F) cheer

A. A and B B. B and E C. A and E D. C and D E. A and D

Answer: Option B
Explanation: One is most likely to emerge successfully from an adverse situation if one is courageous. So also when one suffers.
2. The natural beauty of the _____ location and its lush vegetation and wildlife have been a rich source opportune of inspiration for artists and naturalists. (A) chaotic (B) scenic (C) picturesque (D) rustic (E) opulent (F) terrestrial

A. A and D B. D and E C. B and C D. E and F E. A and B

Answer: Option C
Explanation: A scenic or a picturesque location with its natural beauty is quite likely to inspire artists and naturalists.
Error Correction (Underlined Part)
1. He called the fire service when he has seen the house on fire.

A. he will see the house B. the house has been seen C. he saw the house D. the house is seen E. No correction required

Answer: Option C
Explanation: The first part of the sentence, the main clause, is in the past tense as 'called' is used. Hence what follows in the subordinate clause should also be in past tense. 'has seen' is in the present perfect and hence is wrong. 'Saw' is the contact usage.
2. Real courage and the most complete diligence in his work are the reasons for his success.

A. his complete diligence on work B. the most complete diligence in work C. his complete diligence on his work D. complete diligence in his work E. No correction required

Answer: Option D
Explanation: The adjective 'complete' does not take the comparative degree or the superlative degree. Hence the use of 'most' is inappropriate.
Passage Completion
Direction (1 - 3): In economics, the term recession generally describes the reduction of a country’s Gross Domestic Product (GDP) for at least two quarters. A recession is…( I )…by rising unemployment, an increase in government borrowing,…( II)…, of share and stock prices, and falling investment. All of these characteristics have effects on people. Some recessions have been anticipated by stock market declines. The real estate market also usually…( III )…before a recession.
1. Choose the best word in place of ( I ) from the given passage

A. imagined B. depict C. shown D. visualized E. characterized

Answer: Option E
2. Choose the best word in place of ( II ) from the given passage

A. Increase B. variance C. more D. decrease E. abundance

Answer: Option D
Substitution
1. A person who can be cheated easily.

A. egoist B. client C. credulous D. faithful

Answer: Option C
2. One who cuts precious stones.

A. drover B. oculist C. philatelist D. lapidist

Answer: Option D
Idioms and Phrases
1. To be fair and square pays in the long run.

A. Worthy B. successful C. honest D. honest means

Answer: Option C
2. To scale up

A. to divide B. to discuss C. to deliver D. to measure

Answer: Option D
Antonyms
1. DISSUADE

A. encourage B. intrigue C. trigger D. tarnish E. embellish

Answer: Option A
Explanation: Dissuade is to discourage, the word encourages (persuade) which conveys the opposite meaning is its antonym.
2. NOTORIETY

A. ill-fame B. celebrity C. nickname D. fame E. sobriquet

Answer: Option D
Explanation: The frame is the antonym of notoriety (the state of being famous for something bad).
Sentence Arrangement
1. A policeman (P) to abide (Q) if he has to do well (R) by the strict letters of the law (S) cannot afford

A. PRQS B. SPRQ C. RQPS D. QSPR

Answer: Option D
2. The effectiveness of a film (P) the needs of the audience (Q) is judged by (R) and its relation to (S) It's theme

A. QSRP B. PSQR C. PQRS D. QPRS

Answer: Option A

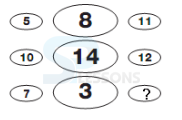
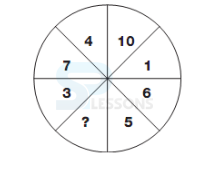
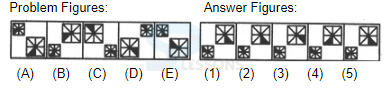
Number Coding
1. In a certain code language, if INFER = 25 and JERSEY = 28, then CHOICE =?

A. 34 B. 39 C. 41 D. 47 E. 49

Answer: Option A
Explanation: I N F E R => 9 + 14 + 6 + 5 + 18 = 52. In this, the reverse of the sum of the place values of the letters in the word is given as its code. J E R S E Y => 10 + 5 + 18 + 19 + 5 + 25 = 82 and the code is 28. Similarly, C H O I C E => 3 + 8 + 15 + 9 + 3 + 5 = 43 The code is 34.
2. If each alphabet is assigned a sequential numerical value in terms of odd numbers on the basis of their position in the English alphabet; viz. A = 1; B = 3; C = 5 and so on. What will be the value of the word DESK?

A. 76 B. 74 C. 64 D. 68 E. None of these

Answer: Option B
Explanation: According to the question, the value of all the letters will be its sequential numerical value as in English alphabet + the no. of letters before it in the English alphabet. Hence D = 4 + 3 = 7, S = 19 + 18 = 37, E = 5 + 4 = 9, K = 11 + 10 = 21. Numerical value of DESK = 7 + 9 + 37 + 21 = 74.
3. If SNOW is coded as 7100, then WALL will be coded as

A. 5000 B. 4700 C. 4800 D. 4000

Answer: 4800
Explanation: Here, Total of all the individual letters’ numeric position is done and just to add some more complexity 00 is appended at the end. S=19, N=14, O=15 and W=23. So 19+14+15+23= 7100.
Inserting Correct Mathematical Sign
1. Find out the two signs to be interchanged for making following equation correct: 5 + 3 x 8 - 12 ÷ 4 = 3

A. + and - B. - and ÷ C. + and x D. + and ÷

Answer: Option B
Explanation: On interchanging - and ÷, we get the equation as 5 + 3 x 8 ÷ 12 - 4 = 3 or 5 + 3 x 2/3 - 4 = 3 or 3 = 3, which is true.
2. Given interchanges : Signs + and x and numbers 4 and 5.

A. 5 x 4 + 20 = 40 B. 5 x 4 + 20 = 85 C. 5 x 4 + 20 = 104 D. 5 x 4 + 20 = 95

Answer: Option C
Explanation: On interchanging + and x and 4 and 5 in (c), we get the equation as 4 + 5 x 20 = 104 or 104 = 104,
3.Given intercharges : Signs - and ÷ and numbers 4 and 8.

A. 6 - 8 ÷ 4 = - 1 B. 8 - 6 ÷ 4 = 1 C. 4 ÷ 8 - 2 = 6 D. 4 - 8 ÷ 6 = 2

Answer: Option C
Explanation: On interchanging - and ÷ and 4 and 8 in (c), we get the equation as 8 - 4 ÷ 2 = 6 or 8 - 2 = 6 or 6 = 6.
Mutual Relation Problem
1. Daya has a brother Anil, Daya is the son of Chandra. Bimal is Chandra`s father. In term of relationship, what is Anil of Bimal?

A. Son B. Grandson C. Brother D. Grandfather

Answer: Option B
Explanation: Anil is the brother of Daya and Daya is the son of Chandra. So, Anil is the son of Chandra. Now, Bimal is the father of Chandra. So, Anil is the grandson of Bimal.
2. Rahul`s mother is the only daughter of Monika`s father. How is Monika`s husband related to Rahul?

A. Uncle B. Father C. Grandfather D. Brother E. Data inadequate

Answer: Option B.
Explanation: Clearly, the only daughter of Monika's father is Monika herself. So, Rahul's mother is Monika. Thus, Monika's husband is the father of Rahul.
3. If (i) M is the brother of N; (ii) B is the brother of N; (iii) M is the brother of D, then which of the following statements is definitely true?

A. N is the brother of B B. N is the brother of D C. M is the brother of B D. D is the brother of M E. None of these

Answer: Option C.
Explanation: M is the brother of N and B is the brother of N. So, M is the brother of B.
Number Puzzle
1. Which number replaces the qtestion mark?

A. 8 B. 6 C. 4 D. 2

Answer: Option C
Explanation: In each row of the diagram, the sum of the left and right-hand digits, minus the central digit is always 8.
2. Which number replaces the qtestion mark?

A. 11 B. 15 C. 8 D. 7

Answer: Option C
Explanation: Divide the circle, horizontally and vertically, to give 4 quarters. The sum of the numbers in the segments of each quarter equals 11.
3. Which number replaces the qtestion mark?

A. 56 B. 45 C. 39 D. 33

Answer: Option C
Explanation: Moving from left to right, add 6 to the first number to get the next one along, then 8, 10 and 12 to complete the sequence.
Human Relation
1. Lakshmi and Meena's are Rohan's wives. Shalini is Meena's step-daughter. How is Lakshmi related to Shalini?

A. Sister B. Mother-in-Law C. Mother D. Step-mother E. None of these

Answer: Option C.
Explanation: Shalini is Meena's step-daughter means Shalini is the daughter of the other wife of Rohan. So, Shalini is the daughter of Lakshmi or Lakshmi is the mother of Shalini.
2. A party consists of a grandmother, father, mother, four sons, and their wives and one son and two daughters to each of the sons. How many females are there is all?

A. 14 B. 16 C. 18 D. 24 E. None of these

Answer: Option A
Explanation: Grandmother is one female, the mother is another, wives of four sons are the four females and two daughters of all four sons are eight females. So, in all there are 1 + 1 + 4 + 8 = 14 females.
3. Rajan is the brother of Sachin and Manick is the father of Rajan. Jagat is the brother of Priya and Priya is the daughter of Sachin. Who is the uncle of Jagat?

A. Rajan B. Sachin C. Manick D. None of these

Answer: Option A
Explanation: Jagat is the brother of Priya and Priya is the daughter of Sachin. So, Jagat is the son of Sachin. Now, Rajan is the brother of Sachin. Thus, Rajan is the uncle of Jagat.
Non-Verbal Reasoning
1. Select a figure from amongst the Answer Figures which will continue the same series as established by the five Problem Figures.

A. 1 B. 2 C. 3 D. 4 E. 5

Answer: Option A
Explanation: Both the larger and the smaller squares move to the adjacent corner ACW in each turn. Also, the shading in the smaller square moves 1, 2, 3, 4, 5, ... steps ACW sequentially and the shading in the larger square moves 1, 2, 3, 4, 5,.... steps CW sequentially.
2. Select a figure from amongst the Answer Figures which will continue the same series as established by the five Problem Figures.

A. 1 B. 2 C. 3 D. 4 E. 5

Answer: Option D
Explanation: In each step, the CW-end element moves to the ACW-end position.
3. Select a figure from amongst the Answer Figures which will continue the same series as established by the five Problem Figures.

A. 1 B. 2 C. 3 D. 4 E. 5

Answer: Option C
Explanation: In each step, the element at the upper-right position gets enlarged, inverts vertically and reaches the lower-left corner; the existing element at the lower-left position, is lost and a new small element appears at the upper-right position.
Distance and Direction Sense Test
1. Bala walked 25km towards west, took a left turn and walked 15km. He again took a left turn and walked 30km. He then took a right turn and stopped. Now he was facing which direction?

A.West B.East C.South D.North E.None of these

Answer: Option C.
Explanation:

2. Raghav starts walking in the south direction and walks a distance of 7 meters. Now he took a left turn and walk 6m. Again he takes a left turn and walk 15m and reached a point P. Find the distance between starting point and P and in which direction is the person from the initial point.

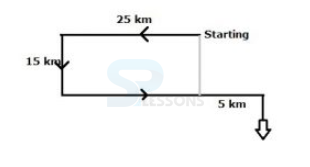
A.10m, southeast B.10m, northeast C.20m, northwest D.20m, southwest E.None of these

Answer: Option B.
Explanation:

3. A person starts walking from a point A in the north direction and after covering 20 meters, he took a right turn and walk 20 meters more. After that, he turns to his right and walks 40 meters before turning to left and walks 20 meters more. After that, he took a left turn and walks 10 meters and finally took a right turn and walk 50 meters and stopped at point B. Now he is facing which direction?

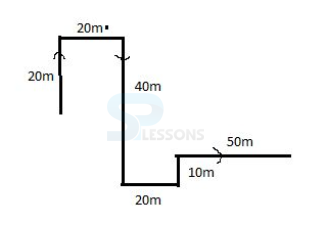
A. east B. west C. north D. south E. None of these

Answer: Option A
Explanation:

Mathematical Operations (Assigning Value to Arithmetic Sign)
1. It being given that : > denotes +, < denotes -, + denotes +, – denotes =, = denotes less than’ and x denotes ‘greater than’, find which of the following is a correct statement.

A. 3 + 2 > 4 < 9 + 3 < 2 B. 3 > 2 > 4 = 18 + 3 < 1 C. 3 > 2 < 4 x 8 + 4 < 2 D. 3 + 2 < 4 x 9 + 3 < 3

Answer: Option C
2. If x stands for ‘addition’, + stands for ‘subtraction’, + stands for ‘multiplication’ and – stands for ‘division’, then 20 x 8 + 8 – 4 + 2 – ?

A. 80 B. 25 C. 24 D. 5

Answer: Option C
3. If – means x, x means +, + means 4, and + means then 40x 12 + 3- 6 + 60 = ?

A. 7.95 B. 16 C. 44 D. 479.95 E. None of these

Answer: Option E
Analogy
1. Melt: Liquid:: Freeze:?

A. Ice B. Condense C. Solid D. Force

Answer: Option C
Explanation: As on melting, the liquid is formed similarly on freezing solid is formed.
2. Cloth: Mill:: Newspaper:?

A. Editor B. Reader C. Paper D. Press

Answer: Option D
Explanation: As Cloth is made in a Mill, similarly Newspaper is printed in the press.
3. Race: Fatigue:: Fast:?

A. Food B. Laziness C. Hunger D. Race

Answer: Option C
Explanation: As the result of Race is Fatigue similarly the result of Fast is Hunger.
Numerical Series
1. Look at this series: 21, 9, 21, 11, 21, 13, 21, ... What number should come next?

A. 14 B. 15 C. 21 D. 23

Answer: Option B
Explanation: In this alternating repetition series, the random number 21 is interpolated every other number into an otherwise simple addition series that increases by 2, beginning with the number 9.
2. Look at this series: 3, 4, 7, 8, 11, 12, ... What number should come next?

A. 7 B. 10 C. 14 D. 15

Answer: Option D
Explanation: This alternating addition series begins with 3; then 1 is added to give 4; then 3 is added to give 7; then 1 is added, and so on.
3. Look at this series: 8, 22, 8, 28, 8, ... What number should come next?

A. 9 B. 29 C. 32 D. 34

Answer: Option D
Explanation: This is a simple addition series with a random number, 8, interpolated as every other number. In the series, 6 is added to each number except 8, to arrive at the next number.
Tallest, Youngest Relation
1. There are five friends --- Sachin, Kunal, Mohit, Anuj and Rohan. Sachin is shorter than Kunal but taller than Rohan. Mohit is the tallest. Anuj is a little shorter than Kunal and little taller than Sachin. Who is taller than Anuj but shorter than Mohit?

A. Kunal B. Rohan C. Sachin D. Data inadequate E. None of these

Answer: Option A
Explanation: Let us denote the five boys by the first letter of their names, namely S, K, M, A, and R. Then, R < S < K < M and S < A < K. R < S < A < K < M. Kunal is taller than Anuj but shorter than Mohit.
2. (i) There is a group of five girls. (ii) Kamini is second in height but younger than Rupa. (iii) Pooja is taller than Monika but younger in age. (iv) Rupa and Monika are of the same age but Rupa is tallest between them. (v) Neelam is taller than Pooja and elder Rupa. To answer the question "who is the youngest person in the group", which of the given statements is superfluous?

A. Only (i) B. Only (ii) C. Only (v) D. Either (i) or (iv) E. None of these

Answer: Option A.
Explanation: We first find the sequence of height : By (iii), we have: M < P. By (v), we have : P < N. Now, Rupa is tallest and Kamini is second in height. So, the sequence of heights is : M < P < N < K < R. Now, we determine the age sequence : By (ii), we have: K < R. By (iii), we have : P < M. By (iv), we have : R = M. By (v), we have : R < N. So, the sequence of ages is : N < R = M < K < P or N < R = M < P < K. Clearly, only statement (i) is not necessary. Hence, the answer is (a).
3. There are five friends --- Sachin, Kunal, Mohit, Anuj, and Rohan. Sachin is shorter than Kunal but taller than Rohan. Mohit is the tallest. Anuj is a little shorter than Kunal and little taller than Sachin. Who is the second tallest?

A. Sachin B. Kunal C. Anuj D. Rohan E. None of these

Answer: Option B.
Explanation: Let us denote the five boys by the first letter of their names, namely S, K, M, A, and R. Then, R < S < K < M and S < A < K. R < S < A < K < M. Kunal is second tallest.
Number Ranking & Time Sequence Test
1. Aruna ranks twelfth in a class of forty-six, what will be her rank from the last?

A. 33 B. 34 C. 35 D. 37 E. None of these

Answer: Option C
Explanation: Number of students behind Aruna in rank = (46 - 12) = 34. So, Aruna is 35th from the last.
2. Manoj and Sachin are ranked seventh and eleventh respectively from the top in a class of 31 students. What will be their respective ranks from the bottom in the class?

A. 20th and 24th B. 24th and 20th C. 25th and 21st D. 26th and 22nd E. None of these

Answer: Option C
Explanation: Number of students behind Manoj in rank = (31 - 7) = 24. So, Manoj is 25th from the bottom. Number of students behind Sachin in rank = (31 - 11) = 20. So, Sachin is 21st from the bottom.
3. Ravi is 7 ranks ahead of Sumit in a class of 39. If Sumit's rank is seventeenth from the last, what is Ravi's rank from the start?

A. 14th B. 15th C. 16th D. 17th

Answer: Option C
Explanation: Sumit is 17th from the last and Ravi is 7 ranks ahead of Sumit. So, Ravi is 24th from the last.
Coding and Decoding
1. If KEYS= MDAR, then LOCK= ?

A. NEJJ B. NNEJ C. JENN D. JENJ

Answer: Option B +2 Increment and -decrement in the next letter. So, K=M, E=D, Y=A, and S=R.
2. In a certain language, CAP is coded as 66, how will PEN be coded

A. 40 B. 66 C. 80 D. 46

Answer: Option D This is an interesting question and you will often get confused. Because even if you try to add the numeric value you won’t get the answer. But here reverse numeric value concept is used. So, in this question, the reverse numeric values are considered and added. C=24, A=26, P=11. 24+26+11=61 and the same logic for PEN. P=11, E=22 and N=13. Answer=46
3. If the MOUSE is coded as ONUFT, then CLOCK will be coded as

A. MDOLD B. MDPLD C. NDOLD D. MDOLE

Answer: Option A Grouping. So here grouping of letters is done. First 2 letters- M and O are grouped and last 2 letters S and E are grouped. After grouping, +1 is added and the position of the letters is interchanged. Like in MO group, +1 is added to the result will be NP and then the letters are interchanged and so the result for the 1st group will be PN. Same for the second group and the middle odd letter is as it is.
Assign Artificial Values to Mathematical Digit
1. If + means ÷, ÷ means –, – means x and x means +, then— 20 + 5 ÷ 7 x 6 – 8 = ?

A 51 B 59 C 37 D 45 E None of these

Answer: Option D
2. If 'p' means '–', 'q' means '+', 'r' means '÷' and 's' means 'x', then— 16 p 4 q 5 s 8 r 2 = ?

A –8 B 32 C 20 D 12 E None of these

Answer: Option B
3. If + means x, – means ÷, x means – and ÷ means +, then— 2 + 15 ÷ 15 – 3 x 8 = ?

A 43 B 27 C 35 D 28 E None of these

Answer: Option B

Simple Interest
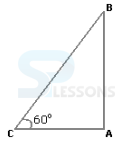
1. A sum of Rs. 2665 is lent into two parts so that the interest on the first part for 8 years at 3% per annum may be equal to the interest on the second part for 3 years at 5% per annum. Find the second sum?

A. Rs.1678 B. Rs.1640 C. Rs.2341 D. None

Answer: Option B
Explanation: (x*8*3)/100 = ((2665 - x)*3*5)/100 24x/100 = 39975/100 - 15x/100 39x = 39975 => x = 1025 Second sum = 2665 – 1025 = 1640
2. If A lends Rs.3500 to B at 10% per annum and B lends the same sum to C at 11.5% per annum then the gain of B in a period of 3 years is?

A. Rs.107.50 B. Rs.115.50 C. Rs.157.50 D. Rs.177.50

Answer: Option C
Explanation: (3500*1.5*3)/100 => 157.50
3. If Rs.450 amount to Rs.540 in 4 years, what will it amount to in 6 years at the same rate % per annum?

A. Rs.575 B. Rs.675 C. Rs.585 D. Rs.685

Answer: Option C
Explanation: 90 = (450*4*R)/100 R = 5% I = (450*6*5)/100 = 135 450 + 135 = 585
Height and Distance
1. The angle of elevation of a ladder leaning against a wall is 60° and the foot of the ladder is 4.6 m away from the wall. The length of the ladder is:

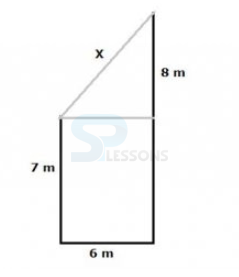
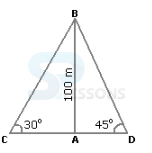
A. 2.3 m B. 4.6 m C. 7.8 m D. 9.2 m

Answer: Option D
Explanation: Let AB be the wall and BC be the ladder.
Then, ACB = 60° and AC = 4.6 m. [latex]\frac {AC}{BC}[/latex] = cos 60° = [latex]\frac {1}{2}[/latex] BC = 2 x AC =(2 x 4.6) m = 9.2 m.
2. From a point P on level ground, the angle of elevation of the top tower is 30°. If the tower is 100 m high, the distance of point P from the foot of the tower is:

A. 149 m B. 156 m C. 173 m D. 200 m

Answer: Option C
Explanation: Let AB be the tower.
Then, APB = 30° and AB = 100 m. [latex]\frac {AB}{AP}[/latex] = tan 30° = [latex]\frac {1}{\sqrt {3}}[/latex] AP = (AB x[latex]\sqrt {3}[/latex]) m = 100[latex]\sqrt {3}[/latex] m = (100 x 1.73) m = 173 m.
3. Two ships are sailing in the sea on the two sides of a lighthouse. The angle of elevation of the top of the lighthouse is observed from the ships are 30° and 45° respectively. If the lighthouse is 100 m high, the distance between the two ships is:

A. 173 m B. 200 m C. 273 m D. 300 m

Answer: Option C
Explanation: Let AB be the lighthouse and C and D be the positions of the ships.
Then, AB = 100 m, ACB = 30° and ADB = 45°. [latex]\frac {AB}{AC}[/latex] = tan 30° = [latex]\frac {1}{\sqrt {3}}[/latex] => AC = AB x[latex]\sqrt {3}[/latex] = 100[latex]\sqrt {3}[/latex] m. [latex]\frac {AB}{AD}[/latex] = tan 45° = 1 => AD = AB = 100 m. CD = (AC + AD) = (100[latex]\sqrt {3}[/latex] + 100) m = 100([latex]\sqrt {3}[/latex] + 1) = (100 x 2.73) m = 273 m.
Volume and Surface Area
1. The edges of a cuboid are 4 cm; 5 cm and 6 cm. Find its surface area?

A. 120 cm[latex]^ {2}[/latex] B. 148 cm[latex]^ {2}[/latex] C. 74 cm[latex]^ {2}[/latex] D. 15 cm[latex]^ {2}[/latex]

Answer: Option B
Explanation: 2(4*5 + 5*6 + 4*6) = 148
2. The area of the floor of a room is 20 m[latex]^ {2}[/latex] that of a longer wall 15 m[latex]^ {2}[/latex] and of the shorter wall 12 m[latex]^ {2}[/latex], find the edge of the new cube?

A. 450 m[latex]^ {3}[/latex] B. 100 m[latex]^ {2}[/latex] C. 60 m[latex]^ {3}[/latex] D. 400 m[latex]^ {3}[/latex]

Answer: Option C
Explanation: lb = 20 ; lh = 15 ; fh = 12 (lbh)[latex]^ {2}[/latex] = 20 * 15 * 12 => lbh = 60 m[latex]^ {3}[/latex]
3. The area of a base of a cone is 30 cm[latex]^ {2}[/latex]. If the height of the cone is 6cm, find its volume?

A. 120 cm[latex]^ {3}[/latex] B. 40 cm[latex]^ {3}[/latex] C. 50 cm[latex]^ {3}[/latex] D. 60 cm[latex]^ {3}[/latex]

Answer: Option D
Explanation: πr[latex]^ {2}[/latex] = 30 h = 6 1/3 * 30 * 6 = 60.
Races and Games
1. A can run a kilometer race in 4 1/2 min while B can run same race in 5 min. How many meters start can A give B in a kilometer race, so that the race mat end in a dead heat?

A. 150 m B. 125 m C. 130 m D. 100 m

Answer: Option D
Explanation: A can give B (5 min - 4 1/2 min) = 30 sec start. The distance covered by B in 5 min = 1000 m. Distance covered in 30 sec = (1000 * 30)/300 = 100 m. A can give B 100m start.
2. In a game of billiards, A can give B 20 points in 60 and he can give C 30 points in 60. How many points can B give C in a game of 100?

A. 50 B. 40 C. 25 D. 15

Answer: Option C
Explanation: A Scores 60 while B scores 40 and C scores 30. The number of points that C scores when B scores 100 = (100 * 30)/40 = 25 * 3 = 75. In a game of 100 points, B gives (100 - 75) = 25 points to C.
Simplification
1. 9000 + 16 2/3 % of ? = 10500

A. 1500 B. 1750 C. 9000 D. 7500 E. None of these

Answer: Option C
Explanation: 9000 + 16 2/3 % of ? = 10500 => 9000 + 50/3 % of ? = 10500 50/(3 * 100) of ? = 1500 => ? = 1500 * 6 ? = 9000
2. 0.003 * ? * 0.0003 = 0.00000027

A. 9 B. 3 C. 0.3 D. 0.03 E. None of these

Answer: Option C
Explanation: 0.003 * ? * 0.0003 = 0.00000027 3/1000 * ? * 3/10000 = 3/1000 * 3/1000 * 3/100 ? = 3/10 = 0.3
Time and Distance
1. A train 240 m in length crosses a telegraph post in 16 seconds. The speed of the train is?

A. 50 kmph B. 52 kmph C. 54 kmph D. 56 kmph

Answer: Option C
Explanation: S = 240/16 * 18/5 = 54 kmph
2. Two trains each 250 m in length are running on the same parallel lines in opposite directions with the speed of 80 kmph and 70 kmph respectively. In what time will they cross each other completely?

A. 10 sec B. 11 sec C. 12 sec D. 14 sec

Answer: Option C
Explanation: D = 250 m + 250 m = 500 m RS = 80 + 70 = 150 * 5/18 = 125/3 T = 500 * 3/125 = 12 sec
Chain Rule
1. 20 women take 20 minutes to roll 20 chapattis. How many chapattis can 400 women roll in 400 minutes?

A. 20 B. 2000 C. 4000 D. 8000

Answer: Option D.
Explanation: Men = M; Days = D; Time/Hours = T; Work = W M1D1T1W2 = M2D2T2W1 Note that - W2 is on left side and W1 is on right side ∴ 20 women x 20 minutes x ? = 400 women x 400 minutes x 20 chapattis ∴ ? = 8000 chapattis = Are rolled by 400 women in 400 minutes.
2. A building is under construction and the task of paving the blocks is given to a group of men. 40 men can finish the given task in 96 days, working 9 hours/day. If 48 men take up the assignment and commit to finishing it in 45 days, how many hours will they need to work per day?

A. 16 B. 18 C. 24 D. 27

Answer: Option A
Explanation: Men = M; Days = D; Time/Hours = T; Work = W M1D1T1W2 = M2D2T2W1 Note that - W2 is on left side and W1 is on right side Take work done = 1 ∴ 40 men x 96 days x 9 hours x 1 = 48 men x 45 days x ? hours x 1 ∴ ? = 16 hours = 48 men need to work these many hours per day
Permutation and Combination
Surds and Indices
1. (17[latex]^ {14}[/latex] * 17[latex]^ {16}[/latex]) / 17[latex]^ {-8}[/latex] = ?

A. 17[latex]^ {28 }[/latex] B. 17[latex]^ {24 }[/latex] C. 17[latex]^ {26 }[/latex] D. 17[latex]^ {22 }[/latex] E. None of these

Answer: Option D
Explanation: ? = 17[latex]^ {14+16-8}[/latex] = 17[latex]^ {22}[/latex]
2. (3[latex]^ {-3 }[/latex] * 9[latex]^ {5/2}[/latex]) / (27[latex]^ {2/3}[/latex] * 3[latex]^ {-4}[/latex]) = ?

A. 3 B. 9 C. 81 D. 21 E. None of these

Answer: Option C
Explanation: (3[latex]^ {-3}[/latex] * 9[latex]^ {5/2}[/latex]) / (27[latex]^ {2/3}[/latex] * 3[latex]^ {-4}[/latex]) = [3[latex]^ {-3}[/latex] *([latex] (3^{2})^{5/2})[/latex]] / [([latex](3^{3})^{2/3})[/latex] * 3[latex]^ {-4}[/latex]] = (3[latex]^ {-3}[/latex] * 3[latex]^ {5}[/latex]) / (3[latex]^ {2 }[/latex]* 3[latex]^ {-4}[/latex]) = (3[latex]^ {-3+5}[/latex])/(3[latex]^ {2-4}[/latex]) = 3[latex]^ {2}[/latex]/3[latex]^ {-2}[/latex] = 3[latex]^ {2 }[/latex]* 3[latex]^ {2}[/latex] = 81.
Pipes and Cistern
1. Pipe P can fill a cement tank in 24 hours. However, there is a leakage at the bottom of the tank due to which the Pipe P takes 12 hrs longer and fills it in 36 hours. How long would this leakage take to empty the entire tank?

A. 48 hours B. 60 hours C. 72 hours D. 96 hours

Answer: Option C.
Explanation: Normally, Pipe P can fill the cement tank in 24 hours. So in 1 hour it fills =[latex]\frac {1}{24}[/latex] part of tank Due to leak, Pipe P can fill the tank in 36 hours. So in 1 hour it actually fills =[latex]\frac {1}{36}[/latex] part of tub ∴ Water removed by the leak in 1 hour =[latex]\frac {1}{24}[/latex] - [latex]\frac {1}{36}[/latex] = [latex]\frac {1}{72}[/latex] ∴ Leak empties the tank in 72 hours.
2. Pipe A takes 38 hours to fill a tank alone while Pipe B takes half the time taken by Pipe A to fill the same tank alone. The leakage C can empty the entire tank in 133 hours. How many hours will it take to fill the tank if Pipe A and B are opened together and leakage C is also allowed to empty the tank simultaneously?

A. 14 hours B. 19 hours C. 28 hours D. 95 hours

Answer: Option A
Explanation: Tank filled by A in 1 hour = [latex]\frac {1}{38}[/latex] Tank filled by B in 1 hour (A takes 38 hrs, so B would take 19 hrs) =[latex]\frac {1}{19}[/latex] Tank emptied by leakage C in 1 hour =[latex]\frac {1}{133}[/latex] Tank filled by all 3 openings together in 1 hour =[latex]\frac {1}{38}[/latex]+[latex]\frac {1}{19}[/latex] -[latex]\frac {1}{133}[/latex] Making denominators common, Tank filled by all 3 pipes together in 1 hour =[latex]\frac {3.5}{133}[/latex]+[latex]\frac {7}{133}[/latex] -[latex]\frac {1}{133}[/latex] =[latex]\frac {9.5}{133}[/latex]=[latex]\frac {1}{14}[/latex] So the entire tank is full in [latex]\frac {14}{1}[/latex] = 14 hours -------------> Inverse or reciprocal of [latex]\frac {1}{14}[/latex]
Boats and Streams
1. A motorist can go downstream at 18 km/hr and upstream at 10 km/hr. Find the speed of the stream and the speed of the motorist in still waters.

A. Motorist = 8 km/hr ; Stream = 28 km/hr B. Motorist = 10 km/hr ; Stream = 5 km/hr C. Motorist = 14 km/hr ; Stream = 4 km/hr D. Motorist = 28 km/hr ; Stream = 8 km/hr

Answer: Option C.
Explanation: Man's/Boat's Speed = X Stream/Current/River Speed = Y ∴ Downstream speed = X + Y Upstream speed = X - Y X+Y = 18 km/hr and X-Y = 10 km/hr Adding them we get, X+Y+X-Y = 28 km/hr ∴ X = 14 km/hr = Speed of Motorist Y=18-14 = 4 km/hr = Speed of stream.
2. A boatman rows his boat 48 km upstream and same distance downstream. The boat takes 12 hrs and 8 hrs to go upstream and downstream respectively. Find the speed of the boat in stagnant water and the speed of the stream respectively.

A. 4 km/hr ; 3 km/hr B. 5 km/hr ; 1 km/hr C. 6 km/hr ; 4 km/hr D. 12 km/hr ; 6 km/hr E. Cannot be determined

Answer: Option B
Explanation: Man's/Boat's Speed = X Stream/Current/River Speed = Y ∴ Downstream speed = X + Y Upstream speed = X - Y Downstream Speed = [latex]\frac {Distance covered}{Time taken}[/latex] = [latex]\frac {48}{8}[/latex]= 6 km/hr Upstream Speed = [latex]\frac {Distance covered}{Time taken}[/latex]= [latex]\frac {48}{12}[/latex]= 4 km/hr X+Y = 6 km/hr and X-Y = 4 km/hr Adding them we get, X+Y+X-Y = 10 km/hr ∴ X=5 km/hr = Speed of Boat Y=6-5 = 1 km/hr = Speed of stream
Numbers
1. Five consecutive numbers add up to 335. What will be the sum of largest and smallest number?

A. 134 B. 150 C. 174 D. 226

Answer: Option A
Explanation: Let 5 consecutive numbers be N, N+1, N+2, N+3, N+4 Sum = N+(N+1)+(N+2)+(N+3)+(N+4) = 5N + 10 = 335 ∴ N (Smallest Number) = 65; Largest Number = 65 + 4 = 69 ∴ 65 + 69 = 134 = Sum of largest and smallest number.
2. We reverse a number and form a new one. The old number is 45 less than new number. The sum of the digits of the old number is 9. What is the new number?

A. 36 B. 54 C. 72 D. 81 E. None of the above

Answer: Option C
Explanation: Let the two digits be X and Y. Let the older number be A and newer one be B. A = 10X + Y ∴ B = 10 Y + X From given, B = 45 + A = 45 + 10X + Y 10Y + X = 45 + 10X + Y So, 9Y - 9X = 45; Y - X = 5 ----------------- (1) X + Y = 9 ---------------- (2) Solving (1) and (2), Y = 7; X = 2 So, A = 27; B = 72
Partnership
1. Polly and Jolly jointly buy a tractor. Jolly's investment is one-sixth the investment of Polly. In a profit of Rs. 91000 what will be Polly's share?

A. Rs. 50000 B. Rs. 66000 C. Rs. 72000 D. Rs. 78000

Answer: Option D
Explanation: When the time period is the same, The ratio of investment = Ratio of Profit The ratio of investment of Polly to Jolly = 6:1 = Ratio of Profit The share of Polly in profit =[latex]\frac {6}{6 + 1}[/latex] x 91000 = Rs. 78000
2. Three friends Mohan, Neeraj and Prateek make an equal investment in a business. Neeraj withdraws after just 5 months while Mohan withdraws 3 months after Neeraj. Only Pratik continues for a year. Find the ratio of profits of Mohan, Neeraj, and Pratik respectively, if Mohan's investment was Rs. 216,800/-?

A. 4 : 7 : 1 B. 5 : 8 : 12 C. 8 : 5 : 12 D. 12 : 5 : 8

Answer: Option C
Explanation: When investment is same, The ratio of time = Ratio of Profit Let us denote Mohan by M, Neeraj by N and Prateek by P. Ratio of time periods of M , N and P = 8 : 5 : 12 = Ratio of Profit.
Ratio and Proportion
1. Find the 3rd proportional to 9 and 72.

A. 8 B. 216 C. 576 D. 648

Answer: Option C
Explanation: In a:b:c, 3rd proportional is c. a:b:c can be written as a:b::b:c a:b::b:c can be written as[latex]\frac {a}{b}[/latex] = [latex]\frac {b}{c}[/latex]=> b[latex]^ {2}[/latex] = ac Here, a:b:c = 9:72:c ∴ 72 x 72 = 9 x c ∴ c = [latex]\frac {72 \times 72}{9}[/latex]= 576
2. Find the 4th proportional in 7, 23 and 217?

A. 66 B. 506 C. 713 D. 961

Answer: Option C
Explanation: In a:b::c:d , 4th proportional is d. a:b::c:d can be written as[latex]\frac {a}{b}[/latex] =[latex]\frac {c}{d}[/latex] => d = [latex]\frac {c \times b}{a}[/latex] Here, a:b::c:d = 7:23::217:d ∴ d = [latex]\frac {23 \times 217}{7}[/latex]= 713
Problems on H.C.F and L.C.M.
1. Find the LCM of following three fractions: [latex]\frac {36}{225}[/latex] ,[latex]\frac {48}{150}[/latex] ,[latex]\frac {72}{65}[/latex]

A. [latex]\frac {72}{225}[/latex] B. [latex]\frac {36}{65}[/latex] C. [latex]\frac {144}{5}[/latex] D. [latex]\frac {288}{5}[/latex]

Answer: Option C
Explanation: LCM of fraction = [latex]\frac {LCM of numerators}{HCF of denominators}[/latex] Numerators = 36, 48 and 72. 72 is largest number among them. 72 is not divisible by 36 or 48 Start with table of 72. 72 x 2 = 144 = divisible by 72, 36 and 48 ∴ LCM of numerators = 144 Denominators = 225, 150 and 65 We can see that they can be divided by 5. On dividing by 5 we get 45, 30 and 13 We cannot divide further. So, HCF = GCD = 5 LCM of fraction = [latex]\frac {144}{5}[/latex]
2. Given : Three numbers 17, 42 and 93 Find the largest number to divide all the three numbers leaving the remainders 4, 3, and 15 respectively at the end?

A. 13 B. 17 C. 78 D. 89

Answer: Option A
Explanation: Here greatest number that can divide means the HCF Remainders are different so simply subtract remainders from numbers 17 - 4 = 13; 42 - 3 = 39; 93 - 15 = 78 Now let's find HCF of 13, 39 and 78 By direct observation we can see that all numbers are divisible by 13. ∴ HCF = 13 = required greatest number
Banker’s Discount
1. The banker's gain on a sum due 3 years hence at 12% per annum is Rs. 270. The banker's discount is:

A. Rs. 960 B. Rs. 840 C. Rs. 1020 D. Rs. 760

Answer: Option C
Explanation: T.D.= ([latex]\frac {B.G. \times 100}{R \times T}[/latex]) = Rs. ([latex]\frac {270 \times 100}{12 \times 3}[/latex]) = Rs. 750. B.D. = Rs.(750 + 270) = Rs. 1020.
2. The banker's gain of a certain sum due 2 years hence at 10% per annum is Rs. 24. The present worth is:

A. Rs. 480 B. Rs. 520 C. Rs. 600 D. Rs. 960

Answer: Option C
Explanation: T.D. = [latex]\frac {B.G. \times 100}{Rate \times Time}[/latex]= Rs.[latex]\frac {24 \times 100}{10 \times 2}[/latex] = Rs. 120. P.W. =[latex]\frac {100 \times T.D.}{Rate \times Time}[/latex]= Rs.[latex]\frac {100 \times 120}{10 \times 2}[/latex] = Rs. 600.
Compound Interest
1. Rohit says that, an amount became 4 times in 6 years. His friend wanted to know, how many years will it take for the amount to become 64 times, provided the rate of interest remains same?

A. 12 years B. 16 years C. 18 years D. 24 years

Answer: Option C
Explanation: Initial Amount = P. P becomes 4 times in 6 years ∴ P → 4P in 6 years ∴ 4P → 4 x (4P) = 16P in next 6 years. Continuing this, 16P → 4 x (16P) = 64P in next 6 years. So total time to get to 64 times i.e. 64P = 6+6+6 = 18 years.
2. Sum: 6400 Time period: 6 months The rate of interest: 25% compounded quarterly. Find the interest earned.

A. Rs. 735.5 B. Rs. 815 C. Rs. 825 D. Rs. 855

Answer: Option C
Explanation: Total Amount = P[latex]( 1 + \frac {R}{100})^{2}[/latex] Principal = P = Rs. 6400 For quarterly compound interest, R = [latex]\frac {R}{4}[/latex] and n = 4n Rate of interest, R = [latex]\frac {R}{4}[/latex] = [latex]\frac {25}{4}[/latex] Time period, n = 4T = 4 x 6 months = 4 x[latex]\frac {1}{2}[/latex] years = 2 years Total Amount = 6400 [latex]( 1 + \frac {25}{4 \times 100})^{2}[/latex] = 6400[latex](\frac {425}{400})^{2}[/latex] = 6400 [latex](\frac {17}{16})^{2}[/latex] ∴ Total Amount = Rs. 7225 Compound Interest = Amount - Principle = 7225 - 6400 = Rs. 825
Area
1. The length and breadth of a rectangular piece of fabric are in the ratio 7:4. The length of the fabric is 15 m more than that of the breadth. Find the area that this fabric would cover.

A. 450 sq.m. B. 700 sq.m. C. 850 sq.m. D. 900 sq.m.

Answer: Option B
Explanation: Let the common factor be K ∴ Length = 7K and Breadth = 4K Also, 4K+15m = 7K ∴ K = 5 ∴ Area of Rectangular ground = Length x Breadth = 7K x 4K = 35 x 20 = 700 sq.m.
2. A rectangular piece of paper has an area 840 sq. cm. The length of the side is 48 cm. The rectangle is stretched such that its area becomes 2 [latex]\frac {6}{7}[/latex] times original rectangle. The only dimension that change is the breadth of the rectangle. Find the perimeter of the new rectangle.

A. 1.69 m B. 1.85 m C. 1.96 m D. 2.25 m

Answer: Option C
Explanation: New area = 840 x 2 [latex]\frac {6}{7}[/latex] = 840 x [latex]\frac {20}{7}[/latex]= 2400 sq.cm Area of Rectangle = length x breadth New Breadth =[latex]\frac {New Area}{Length}[/latex] = [latex]\frac {2400}{48}[/latex] = 50 cm Perimeter of new margin = 2(length + new breadth) = 2(48 + 50) = 196cm = 1.96m
3. Ratan takes turns to cycle around the circular garden and through the diameter of the garden on alternate days. His speed each day is 6m/min but when he cycles through the diameter, he takes 1 hr less to cross the park. Find the diameter of the park.

A. 1530 m B. 1680 m C. 1750 m D. 3600 m

Answer: Option B
Explanation: We know that, Time =[latex]\frac {Distance}{Speed}[/latex] Speed = 60m/min = [latex]\frac {60}{60}[/latex] m/sec = 1 m/sec We know that, Time along the park (circumference) - Time along the diameter = 60 minutes ∴[latex]\frac {2πr}{1}[/latex] - [latex]\frac {2r}{1}[/latex] = 60 minutes ∴ 2r ([latex]\frac {22}{7}[/latex]- 1) = 3600 seconds ∴ r = 840m ∴ Diameter = 2 x radius = 1680m.
Time and Work
1. Amish is 5 times as efficient as Brijesh. Amish can finish the work 60 days earlier than Brijesh. If they work individually, how many days would they take to finish the work?

A. Amish = 10 days; Brijesh = 50 days B. Amish = 15 days; Brijesh = 75 days C. Amish = 20 days; Brijesh = 80 days D. Amish = 20 days; Brijesh = 100 days

Answer: Option B
Explanation: The speed of Work / Efficiency ∝ [latex]\frac {1}{Time needed}[/latex] So more the efficiency, less time is needed to do the task. Let us denote Amish by 'A' and Brijesh by 'B' Hence, if A is 5 times faster than B, then B needs 5 times more time than A. Let A need 'n' days to complete the work. So B will need 5n days. Also, 5n – n = 60 ------------------- Given ∴ n = 15 days = Days needed by A to complete work individually Days needed by B to complete work individually = 5n = 5 x 15 = 75 days
2. Recollecting the progress of an assignment, a group of 24 men said that they finished a project together in 10 days. Find the number of days required to complete the same work if 30 men had worked on the same project.

A. 3 days B. 6 days C. 7.5 days D. 8 days

Answer: Option D
Explanation: 24 men complete work in 10 days. ∴ In 1 day work done by 24 men = [latex]\frac {1}{10}[/latex] In 1 day work done by 30 men =? ∴ ? x 24 = [latex]\frac {1}{10}[/latex]x 30 ∴ ? =[latex]\frac {1}{8}[/latex] = Amount of work done by 30 men in one day If A completes work in 'n' days, in 1 day he completes[latex]\frac {1}{n}[/latex] amount of work. Conversely, if A completes[latex]\frac {1}{n}[/latex] amount of work in 1 day, he completes entire work in 'n' days.
Allegation or Mixture
1. A shopkeeper mixes two varieties of pulses with price Rs 420/ Kg and Rs 520/ Kg. The price of the mixture he gets is Rs 480/ Kg. Find the ratio of quantities of the two types of pulses to be mixed?

A. 2:3 B. 2:1 C. 1:3 D. 4:1

Answer: Option A
Explanation:

Ratio of Quantities = 40 : 60 = 2:3
2. While creating the fragrance mix, a shopkeeper mixes some amount of Jasmine essence with 240 liters water. The price of the mixture is Rs. 275/liter. The price of Jasmine essence is Rs 325/liter. What is the quantity of Jasmine essence in the mix?

A. 720 litres B. 1000 litres C. 1200 litres D. 1320 litres

Answer: Option D
Explanation:

Water is free so its price is Rs. 0 Ratio of Water to Essence = 50:275 = 2:11 Water is 2 parts. Hence, 2 parts of water = 240litres. So 11 parts of essence = ? ∴ ? = [latex]\frac {11 \times 240}{2}[/latex] = 1320 litres
Decimal Fraction
1. 0.03 × 0.0124 = ?

A. 3.72 × 10[latex]^ {-6 }[/latex] B. 3.72 × 10[latex]^ {-5}[/latex] C. 3.72 × 10[latex]^ {-3}[/latex] D. 3.72 × 10[latex]^ {-4}[/latex]

Answer: Option D
Explanation: 3 × 124 = 372 Sum of the decimal places in 0.03 and 0.0124 = 2 + 4 = 6 Hence, 0.03 × 0.0124 = 372 × 10[latex]^ {-6}[/latex] = 3.72 × 10[latex]^ {-4}[/latex]
2. 7212 + 15.231 - ? = 6879

A. 359.022 B. 362.02 C. 328.221 D. 348.231

Answer: Option D
Explanation: = 7212 + 15.231 - 6879 = 348.231
Probability
1. A mother has 24 pairs of white socks and 18 pairs of grey socks for her twin children kept in a bag. In a hurry to send the children to school on time, she picks 3 socks randomly. What is the possibility of her picking up the matching pair?

A. [latex]\frac {1}{108}[/latex] B. [latex]\frac {1}{36}[/latex] C. [latex]\frac {7}{36}[/latex] D. 1

Answer: Option D
Explanation: Since a pair has 2 socks in it and there are just two colors - White and grey, when the mother chooses 3 socks, he will surely select 2 socks of the same color - be it grey or white. So possibility = probability = 1
2. Rishabh studies with the help of flashcards. He has a set of 30 flashcards out of which 17 cards are white and rest are grey. 4 white and 5 grey cards are marked ENGLISH. Find the possibility of choosing a grey card or an "ENGLISH" Card randomly from the set.

A. [latex]\frac {9}{13}[/latex] B. [latex]\frac {13}{30}[/latex] C. [latex]\frac {17}{30}[/latex] D. [latex]\frac {22}{30}[/latex]

Answer: Option C
Explanation: Probability = [latex]\frac {What we want}{Total}[/latex] OR = add AND = multiple We want a grey card OR ENGLISH card There are 30 - 17 = 13 grey cards There are 4 + 5 = 9 ENGLISH cards Total cards = 30 Also, 5 grey cards are ENGLISH cards. So probability = [latex]\frac {13}{30}[/latex] +[latex]\frac {9}{30}[/latex]-[latex]\frac {5}{30}[/latex] =[latex]\frac {17}{30}[/latex] Remember: This subtraction is needed a grey card gets counted twice - once in 13 grey cards and once again in 9 ENGLISH cards.
Average
1. Kritika is on a 4 days trip with schoolmates. She had decided to keep her average expense for 4 days at Rs 80. However, at the end of the third day, she realized that her expenses on the first three days were Rs 80, Rs 90, Rs 110 and respectively. How much should she spend on 4th day to ensure that she meets her targeted average expense?

A. Rs. 40 B. Rs. 60 C. Rs. 90 D. Rs. 220

Answer: Option A Average = [latex]\frac {Sum of Observations}{Number of Observations}[/latex] Average = [latex]\frac {80+90+110+ 4th day}{4}[/latex] = 80 ∴ 4th day expenditure = Rs. (320 - 280) = Rs 40
2. Find the average of natural numbers from 1 to 67?

A. 33.5 B. 34 C. 50 D. 67

Answer: Option B
Explanation: Average of first n natural numbers = [latex]\frac {(n+1)}{2}[/latex] Average of natural numbers from 1 to 65 = [latex]\frac {67+1}{2}[/latex]= 34
Stocks and Share
1. Find the market value of the stock if 6% yields 10%.

A. 60 B. 70 C. 80 D. 100

Answer: Option A
Explanation: Let the investment be Rs.100 for an income of Rs.10 Therefore, for an income of Rs.6, the investment = 600/10 = Rs.60
2. What is the investment made if one invests in 15% stock at 50 and earns Rs.2000?

A. 8000 B. 7000 C. 5000 D. 6000

Answer: Option C
Explanation: To earn Rs.15, investment = Rs.50. Hence, to earn Rs.1500, investment = (1500*50)/15 = Rs.5000
Square Root and Cube Root
1. Prashant had some pebbles in his treasure. His friend said, that he could arrange all the 17424 pebbles in a two dimensional square matrix. How many rows did he make?

A. 132 B. 138 C. 141.2 D. 145.8

Answer: Option A
Explanation: Since it is a square matrix, no. of rows = No. of columns Let number of pebbles in each row be P ∴ Number of rows = P Total Pebbles = P x P = P[latex]^{2}[/latex] = 17424 ∴ P = 132 = No. of rows
2. What is 335[latex]^{2}[/latex]?

A. 112225 B. 120225 C. 122225 D. 150225

Answer: Option A
Explanation: To find square of a number ending in 5 Example - 335[latex]^{2}[/latex] 335 ends with 5. So 335[latex]^{2}[/latex] will have 5[latex]^{2}[/latex] = 25 at end Now leave the last digit i.e. 5. We have 33. Add 1 to it. We get 33 + 1 = 34 33 x 34 = 1122 3352 = 112225
Problems on Ages
1. Raj's age is 4 times that of Dhiraj, his cousin. 3 years back, Raj was 5 times as old as Dhiraj. What is his present age?

A. 12 years B. 16 years C. 24 years D. 48 years

Answer: Option D
Explanation: Present day, Let us consider Dhiraj's present age as K years Raj's present age is 4 times Dhiraj's = 4K years 3 years ago, Dhiraj's age = K-3 years Raj's age = 4K-3 years. That time, Raj's age = 5 times Dhiraj's age ∴ 4K-3 = 5(K-3) 4K-3 = 5K-15 ∴ K = 12 years Present age of Raj = 4K = 4 x 12 = 48 years.
2. Referring to his two sons Ram and Shyam, their father says - 12 years ago, Ram was 3 times as old as Shyam. 12 years later, the ratio of ages of Shyam and Ram will be 2:3. What is the present age of Ram?

A. 24 years B. 36 years C. 54 years D. 144 years

Answer: Option B
Explanation: Let us consider Shyam's present age as K years 12 years ago, Shyam's age = K-12 years So Ram's age is 3 times Shyam's = 3(K-12) = (3K-36) years → This age of Ram was 12 years ago Hence, Ram's present age = (3K- 36) + 12 years = (3K-24) years 12 years later from present day, Shyam's age = K+12 years Ram's age = (3K-24) + 12 = (3K-12) years Also,[latex]\frac{Shyam's age}{Ram's age}[/latex] =[latex]\frac{K+12}{3K-12}[/latex]= [latex]\frac{2}{3}[/latex] ∴ K = 20 years = Shyam's present age ∴ Ram's present age = 3K-24 = 3 x 20 - 24 = 36 years