Introduction
Introduction
The article Medak DCCB Study Guide, a preparation guide provides the sample question format of Telangana State DCCB exam. Medak DCCB 2018 – Online Test/Examination, conducted in online Mode, has: a duration of 1 hour, a total of 100 questions, a maximum score of 100 marks, and consists of 3 sections, namely – English Language, Numerical Ability and Quantitative Aptitude/Numerical Ability. The 3 sections are separately timed and the questions can be attempted in any order.
 Pattern
Pattern
For: Assistant Manager
For: Staff Assistant
| Sl. No | Name of Tests (objective) | No. of questions | Max. Marks | Time allotted for each test (Separately timed) |
|---|---|---|---|---|
| 1 | Test of English language. | 30 | 30 | 20 Minutes |
| 2 | Test of Reasoning | 35 | 35 | 20 Minutes |
| 3 | Test of Quantitative Aptitude. | 35 | 35 | 20 Minutes |
| Total | 100 | 100 |
| Sl. No | Name of Tests (objective) | No. of questions | Max. Marks | Time allotted for each test (Separately timed) |
|---|---|---|---|---|
| 1 | Test of English language. | 30 | 30 | 20 Minutes |
| 2 | Test of Reasoning | 35 | 35 | 20 Minutes |
| 3 | Test of Numerical Ability. | 35 | 35 | 20 Minutes |
| Total | 100 | 100 |
Penalty for Wrong Answers:
There will be the penalty for wrong answers marked in the Objective Tests. For each question for which a wrong answer has been given by the candidate one fourth or 0.25 of the marks assigned to that question will be deducted as penalty to arrive at corrected score. If a question is left blank, i.e., no answer is marked by the candidate, there will be no penalty for that question.
 Syllabus
Syllabus
[Click Here] for detailed syllabus.
 Samples
Samples
Prepositions
1. He was vexed ------ Sohan for his behavior.
- A. at
B. to
C. upon
D. with
- A. up
B. about
C. round
D. in
- A. on
B. to
C. for
D. with
- A. The suspect is claimed to have been seen in several cities.
B. The suspect was seen by people in several cities.
C. The suspect has been the people in several cities.
D. The suspect is being seen in several cities.
- A. The suspect is claimed to have been seen in several cities.
B. The suspect was seen by people in several cities.
C. The suspect has been the people in several cities.
D. The suspect is being seen in several cities.
- A. A letter was written to her father by Sugana.
B. A letter was being written by Sugana to her father.
C. A letter was written by Sugana to her father.
D. A letter has been written to her father by Sugana.
- A. Only A
B. Only B
C. Only C
D. A and B
E. None of these
- A. Only A
B. A and B
C. Only B
D. All the three
E. None of these
- A. Only B
B. Only A
C. A and B
D. B and C
E. All the three
- A. suganya opened a almirah
B. full of books
C. and took one of them
D. for reading E. no error
- A. as I was to reach
B. early I left in the airplane
C. instead of
D. going by train E. no error
- A. my friends insisted
B. that I should see the movie
C. from beginning to the end
D. no error
- A. Oppressed
B. Caged
C. Thoughtful
D. Happy
- A. Exile
B. Hate
C. Fade
D. Clean
- A. Malcontent
B. Argument
C. Imposter
D. Clown
- A. may sometimes succeed
B. may sometime succeed
C. sometimes succeed
D. sometimes succeeds
- A. warmer
B. warmest
C. warmer
D. none
- A. by sword
B. by a sword
C. with his sword
D. none
- A. as it is
B. but it is
C. since it could be
D. but it could E. No correction required
- A. the width of
B. so wider than
C. of the width to
D. in width than
E. No correction required
- A. what more reasons
B. that more is the reason
C. what is the reason
D. that the more reasons
E. No correction required
- A. Only A
B. A and B
C. A and C
D. Only C
E. All the three
- A. A and B
B. Only B
C. Only C
D. None of these
E. All the three
- A. Only C
B. B and C
C. A and B
D. Only B
E. None of these
- A. incidence
B. perils
C. potentialities
D. redundancies
- A. refused
B. rejected
C. declaimed
D. denied
- A. departure
B. obsession
C. opprobrium
D. declivity
- A. A and B
B. B and F
C. D and F
D. C and D
E. A and D
- A. C and F
B. B and C
C. A and D
D. B and F
E. D and E
- A. C and F
B. B and C
C. A and D
D. B and F
E. D and E
- A. put themselves
B. keep himself
C. keep oneself
D. put himself
E. No correction required
- A. criterion which is adapted
B. criterion that is adopted
C. criterion that is adapted
D. criterion what is adopted
E. No correction is required
- A. approve of
B. approve in
C. approve on
D. approve at
E. No correction required
- A. imagined
B. depict
C. shown
D. visualized
E. characterized
- A. Increase
B. variance
C. more
D. decrease
E. abundance
- A. weakens
B. initiates
C. awakens
D. strengthens
E. volatile
- A. flora
B. fauna
C. forest
D. vegetation
- A. gift
B. elegy
C. momento
D. epitaph
- A. artist
B. expert
C. musician
D. connoisseur
- A. failed
B. kill someone
C. frustrate
D. bring great happiness
- A. rich food
B. strong critic
C. flattery
D. hungry person
- A. start
B. end
C. forget
D. revive
- A. Round
B. Unimportant
C. Thin
D. Dull
- A. Strange
B. Uneasy
C. Quick
D. Fast
- A. Bashful
B. Boisterous
C. Noisy
D. Heated
- A. QSPR
B. QRPS
C. QPRS
D. QRSP
- A. SRPQ
B. SPQR
C. SPRQ
D. RSPQ
- A. PQSR
B. SRPQ
C. PSRQ
D. PQRS
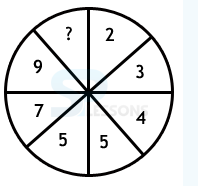
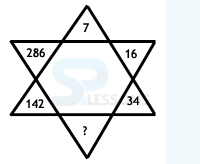
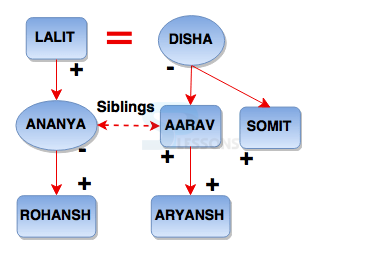
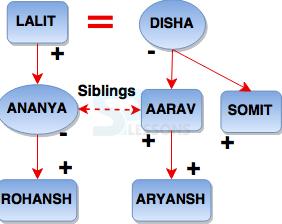
Number Coding
1. If ANY = 40, MANY = 53 then MANIAC = ?
- A. 41
B. 42
C. 43
D. 44
E. 45
- A. 67193237
B. 67132937
C. 67123937
D. 67172937
- A. 32987
B. 92897
C. 38972
D. 32978
- A. 3, 9
B. 3, 8
C. 8, 9
D. 3, 5
- A. x, ÷
B. +, ÷
C. 18 and 5
D. 3 and 9
- A. 165
B. 75
C. 20
D. 3
E. None of these
- A. 35
B. 49
C. 50
D. 63
E. 140
- A. 263
B. 111
C. 242
D. 551
E. 383
- A. 6788
B. 6878
C. 6482
D. 9848
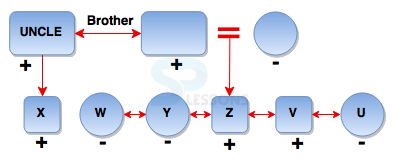
- A. Cousin
B. Uncle
C. Brother-in-law
D. Son-in-law
E. Mother
- A. Nephew
B. Son
C. Son-in-law
D. Father-in-law
E. Cannot be determined
- A. P - R / Q
B. P + R * Q
C. P != R * Q
D. P - R + Q
E. P * R = Q
- A. 10
B. 11
C. 12
D. 13
- A. 75
B. 73
C. 70
D. 60
- A. 38
B. 42
C. 40
D. 37
- A. Niece
B. Mother
C. Sister
D. Sister-in-law
- A. Aunt
B. Grandmother
C. Sister
D. Cousin
- A. Uncle
B. Cousin
C. Sister
D. Niece
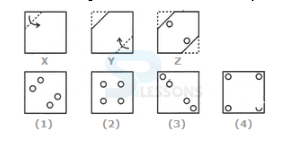
- A. 1
B. 2
C. 3
D. 4
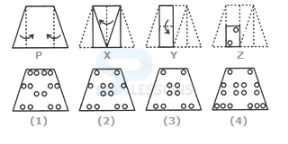
- A. 1
B. 2
C. 3
D. 4
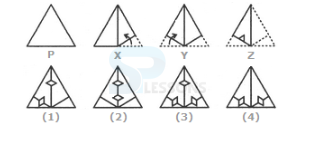
- A. 1
B. 2
C. 3
D. 4
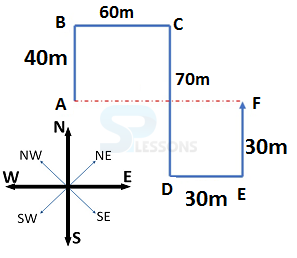
- A. 90 m East
B. 90 m West
C. 90 m South
D. 90 m North
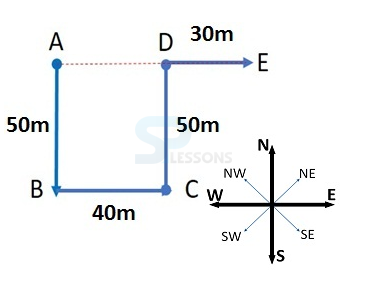
- A. 70 m West
B. 75 m East
C. 75 m North
D. 70 m East
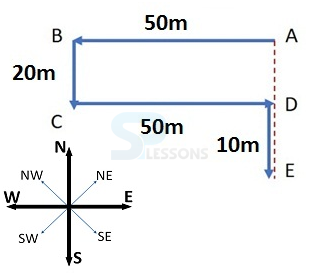
- A. 30 m, South
B. 30 m, North
C. 40 m, South
D. 40 m, North
- A. 5, 1, 2, 3, 4
B. 5, 1, 3, 2, 4
C. 2, 3, 4, 5, 1
D. 2, 5, 1, 4, 3
- A. 2
B. 3
C. 4
D. 1
- A. 3, 2, 4, 5, 1
B. 5, 4, 1, 3, 2
C. 3, 2, 5, 1, 4
D. 5, 1, 2, 3, 4
- A. + and x, 2 and 4
B. + and x, 2 and 6
C. + and x, 4 and 6
D. None of these
- A. + and +, 2 and 3
B. + and +, 2 and 4
C. + and +, 3 and 4
D. No interchange, 3 and 4
- A. x to +, 2 and 4
B. – to +, 2 and 6
C. – to +, 2 and 6
D. x to +, 4 and 6
- A. Friendship
B. Victory
C. Surrender
D. War
- A. China
B. Japan
C. Turkey
D. Malaysia
- A. Adequacy
B. Surplus
C. Competency
D. Import
- A. 4861
B. 4211
C. 4911
D. 4411
- A. 199
B. 233
C. 220
D. 241
- A. 312
B. 216
C. 189
D. 225
- A. P
B. Q
C. S
D. T
E. Can`t be determined
- A. A
B. B
C. D
D. E
E. None of these
- A. B, C only
B. D, B, C only
C. E, B, C only
D. F, B, C only
E. None of these
- A. 37
B. 36
C. 35
D. 34
- A. 40
B. 44
C. 50
D. 55
E. 58
- A. 20th and 24th
B. 24th and 20th
C. 25th and 21st
D. 26th and 22nd
E. None of these
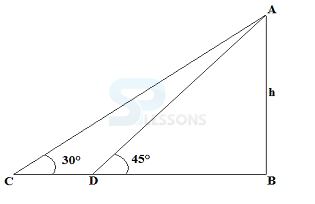
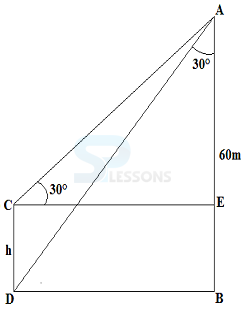
Height and Distance
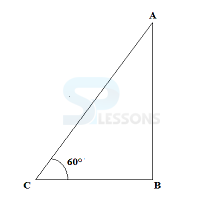
1. The angle of elevation of the sun is 60°. Find the length of the shadow of a man who is 180 cm tall.
- A. 127.27 cm
B. 103.92 cm
C. 311.77 cm
D. None of these
- A. 15 minutes 20 seconds
B. 13 minutes 40 seconds
C. 16 minutes 40 seconds
D. Cannot be determined
- A. 45
B. 30
C. 40
D. 20
- A. 10[latex]^{5}[/latex]
B. 10[latex]^{3}[/latex]
C. 10[latex]^{4}[/latex]
D. 10[latex]^{6}[/latex]
- A. 100kg
B. 90kg
C. 80kg
D. 70kg
- A. 1:3
B. 3:1
C. 2:3
D. 3:2
- A. 1.6020
B. 1.9030
C. 3.9030
D. None of these
- A. 1
B. 3
C. 5
D. 10
- A. 18
B. 19
C. 20
D. 21
- A. 20m
B. 16m
C. 11m
D. 10m
- A. 140m
B. 125m
C. 100m
D. 110m
- A. 100m
B. 80m
C. 90m
D. 110m
- A. 4
B. 9
C. 12
D. 49
- A. 48 paise
B. 54 paise
C. 56 paise
D. 72 paise
- A. 20
B. 30
C. 40
D. 50
- A. 21
B. 12
C. 9
D. 108
E. 101
- A. 8
B. 8!
C. 7!
D. 7
E. 6!
- A. 3
B. 6
C. 24
D. 120
E. 12
- A. 1000
B. 10000
C. 100000
D. 10[latex]^{6}[/latex]
- A. 25
B. 125
C. 250
D. 625
- A. x[latex]^{abc}[/latex]
B. 1
C. x[latex]^{ab + bc + ca}[/latex]
D. x[latex]^{a + b + c}[/latex]
- A. 9 min
B. 10 min
C. 11 min
D. 12 min
- A. 16 hrs
B. 20 hrs
C. 40 hrs
D. 25 hrs
- A. 5260 liters
B. 5760 liters
C. 5846 liters
D. 6970 liters
- A. 1 kmph
B. 5 kmph
C. 8 kmph
D. 3 kmph
- A. 3.12 km
B. 2.88 km
C. 3 km
D. 2 km
- A. 6 kmph
B. 7 kmph
C. 8.5 kmph
D. 8 kmph
- A. Rs.18000
B. Rs.15000
C. Rs.17000
D. Rs.14000
- A. 6 months
B. 8 months
C. 10 months
D. 7 months
- A. Rs.3750
B. Rs.3000
C. Rs.3200
D. Rs.2160
- A. 42
B. 50
C. 55
D. 62
- A. 63: 14: 55
B. 63: 45: 55
C. 14: 14: 15
D. 7: 14: 15
- A. 3
B. 4
C. 5
D. 6
- A. 10/7
B. 10
C. 10/11
D. 11/10
- A. 2/47
B. 3/47
C. 1/48
D. 5/48
- A. 100
B. 121
C. 64
D. 144
- A. Rs. 360
B. Rs. 432
C. Rs. 540
D. Rs. 1080
- A. Rs. 72
B. Rs. 36
C. Rs. 54
D. Rs. 50
- A. Rs. 37
B. Rs. 37.62
C. Rs. 34.38
D. Rs. 38.98
- A. Rs.81.60
B. Rs.160
C. Rs.1081.60
D. Rs.99
- A. 4%
B. 5%
C. 6%
D. 8%
- A. 16
B. 8
C. 12
D. 20
- A. 225 sq m
B. 220 sq m
C. 100 sq m
D. 30 sq m
- A. 650 m
B. 600 m
C. 200 m
D. 300 m
- A. 12 m, 10 m
B. 13 m, 12 m
C. 14 m, 11 m
D. 15 m, 10 m
- A. 16 2/3 days
B. 13 1/3 days
C. 17 1/3 days
D. 16 1/2 days
- A. 18 days
B. 20 days
C. 24 days
D. 30 days
- A. 18 days
B. 12 days
C. 24 days
D. 10 days
- A. 47.095
B. 47.752
C. 47.932
D. 47.95
- A. 6.48 x 10[latex]^{-3}[/latex]
B. 6.48 x 10[latex]^{-4}[/latex]
C. 6.48 x 10[latex]^{-5}[/latex]
D. 6.48 x 10[latex]^{-6}[/latex]
- A. 0.0001
B. 0.001
C. 0.01
D. 0.1
- A. 1/216
B. 1/36
C. 5/9
D. 5/12
E. 7/12
- A. 7/12
B. 5/9
C. 1/36
D. 5/12
E. 8/9
- A. 1/25
B. 1/2
C. 4/13
D. 1/10
E. 9/13
- A. 15
B. 9
C. 18
D. 21
- A. 12.4
B. 14
C. 16
D. 18.6
- A. Rs. 48
B. Rs. 75
C. Rs. 96
D. Rs. 133.33
- A. 7.5%
B. 8%
C. 9.7%
D. None of these
- A. Rs. 83.33
B. Rs. 110
C. Rs. 112
D. Rs. 120
- A. 10
B. 100
C. 1000
D. None of these
- A. 1
B. 2
C. 3
D. None of these
- A. 213444
B. 214344
C. 214434
D. 231444
- A. 32 years
B. 36 years
C. 40 years
D. 48 years
- A. 12 years
B. 14 years
C. 18 years
D. 20 years
- A. 19 years
B. 14 years
C. 33 years
D. 38 years
 Best Books
Best Books
| Name of the Book | Name of the Author | Year of Publication | Book Price in Rs | Book Rating | Get Book |
|---|---|---|---|---|---|
| New Pattern English Language for SBI/ IBPS Bank PO/ SO/ Clerk/ RRB Exams (English, Paperback, Disha Experts) | Disha Experts | 2018 | RS.189/- | ----- | Flipkart |
| Bank PO English Language : 17 Years (2000 - 2016) Chapterwise Solved Papers (English, Paperback, Arihant Experts) | Arihant | 2018 | Rs.201/- | 4.3/5 | Flipkart |
| Bank PO English language Chapterwise Solved Papers - 1723 [Print Replica] Kindle Edition | Think Tank of Kiran Prakashan & KICX | 2018 | Rs.323/- | 3.0/5 | Amazon |
| Winning with English Language 2018 For Competitive Exams: For Banking, IBPS - PO and Clerical, UPSC, IAS, SSC, RAILWAYS, CTET, NDA, CDS, RRB and other (Asktenali Winning Series Book 104) Kindle Edition | Swaminathan Sankaran | 2018 | Rs.76/- | ----- | Amazon |
| Name of the Book | Name of the Author | Year of Publication | Book Price in Rs | Book Rating | Get Book |
|---|---|---|---|---|---|
| 14 Kiran’s Tricky Approach To Competitive Reasoning Verbal & Non Verbal (Fully Solved) 7000+objective Question Logical Reasoning & Analytical Ability—English (Paperback, Kiran) | Kiran | 2016 | RS.590/- | 3/5 | Flipkart |
| IBPS- CWE CLERK SPEED TESTS REASONING | BSC PUBLICATION | ----- | Rs.248/- | 3.6/5 | Flipkart |
| Topic-wise Solved Papers for IBPS/ SBI Bank PO/ Clerk Prelim & Mains (2010-16) Reasoning (English, Paperback, Disha Experts) | Disha Experts | 2017 | Rs.99/- | 4.1/5 | Flipkart |
| Reasoning for IBPS & All Other Examinations (English, Paperback, Sachchida Nand Jha) | Sachchida Nand Jha | 2014 | Rs.90/- | 3.5/5 | Flipkart |
| Reasoning Verbal, Non-Verbal & Analytical - for Competitive Examinations (Englsih, Paperback, Dipak Kumar Yugnirmal) | Dipak Kumar Yugnirmal | 2017 | Rs.400/- | ----- | Flipkart |
| Name of the Book | Name of the Author | Type of Book | Year of Publication | Book Price in Rs | Book Rating | Get Book |
|---|---|---|---|---|---|---|
| Quantitative Aptitude for All Competitive Examinations | Abhijit Guha | Prelims + Mains | 2016 | Rs.359/- | 3.5/5 | Amazon |
| Shortcuts in Quantitative Aptitude with 4 eBooks for Competitive Exams | Disha Experts | Prelims + Mains | 2016 | Rs.45/- | 3.1/5 | Amazon |
| Teach Yourself Quantitative Aptitude | Arun Sharma | Prelims + Mains | 2017 | Rs.259/- | 3.4/5 | Amazon |
| Quantitative Aptitude for competitive examination R S Agarwal 2017-2018 | R S Agarwal | Prelims + Mains | 2017 | Rs.694/- | ----- | Amazon |