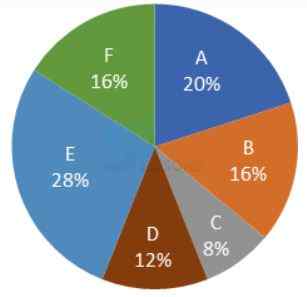
Direction[1-2] : Study the following pie chart carefully and answer the questions given beside.
Given pie chart shows the part of iron ore mined by 6 different machines in a day.
Total amount of iron ore that is mined in a day by 6 machines is 200 kg.

Given pie chart shows the wasted per cent of iron ore which is mined by 6 different machines in a day while extracting Iron from them.
Total amount of wasted iron ore in a day which is mined by 6 machines together is 25 kg.

Amount of mined Iron ore = Extracted amount of Iron + Wasted amount of Iron ore.
1. What is total amount of Iron extracted from the Iron ore which is mined by the machine C and E together?

A. 59 kg B. 25 kg C. 66 kg D. 54 kg

Answer - Option C
Explanation - Total amount of Iron ore mined by machine C
= 200 × [latex]\frac {45}{360}[/latex] = 25 kg
Total wasted amount of Iron ore by machine C = 8% of 25 kg = 2 kg
Total amount of Iron ore mined by machine E
= 200 × [latex]\frac {90}{360}[/latex]= 50 kg
Total wasted amount of Iron ore by machine E = 28% of 25 kg = 7 7 kg
Total amount of Iron extracted = (25 + 50) – (2 + 7) = 75 – 9 = 66 kg
Hence, option C is correct.
2. What is the difference between the total amount of Iron extracted from Iron ore mined by machine D and total amount of Iron ore wasted by machine B and F together?

A. 17 kg B. 10 kg C. 8 kg D. 9 kg

Answer - Option D
Explanation - Total amount of Iron extracted from Iron ore mined by machine D
= 200 × [latex]\frac {36}{360}[/latex] = 20 kg
Wasted amount of Iron ore mined by machine D = 12% of 25 = 3 kg
Amount of Iron extracted from Iron ore mined by machine D = 20 – 3 = 17 kg
Total wasted amount of Iron ore mined by machine B and F together = 32% of 25 = 8 kg
Required difference = 17 – 8 = 9 kg
Hence, option D is correct.

1. 3.25, 6.5, 19.5, 78, 390, ?

A. 2140 B. 2350 C. 2670 D. 2340

Answer - Option D
Explanation - 3.25 * 2 = 6.5
6.5 * 3 = 19.5
19.5 * 4 = 78
2. 68, 117, 61, 124, 54, ?

A. 141 B. 121 C. 151 D. 131

Answer - Option D
Explanation - 68 – 7 = 61
61 – 7 = 54
124 + 7 = 131

1. In an election contested by two parties A and B, party A secured 25 percent of the total votes more than Party B. If party B gets 15000 votes. By how much votes does party B loses the election?

A. 8000 B. 10000 C. 12000 D. 15000

Answer - Option B
Explanation - Let total votes = T and party B gets 15000 votes then party A will get T -15000 votes
T – 15000 – 15000 = 25T/100
T = 40000, so A get 25000 and B gets 15000 votes, so difference = 10000
2. A vendor sells 50 percent of apples he had and throws away 20 percent of the remainder. Next day he sells 60 percent of the remainder and throws away the rest. What percent of his apples does the vendor throw?

A. 20% B. 22% C. 24% D. 26%

Answer - Option D
Explanation - Let total apples be 100
First day he throws = [latex] \frac {50 \times 20}{100}[/latex] = 10 apples
Next day he throws = [latex] \frac {40 \times 40}{100}[/latex] = 16 apples
So total = 26

1. If the difference between the CI and SI on a sum of money at 5% per annum for 2years is Rs.16.Find the Simple Interest?

A. 180 B. 460 C. 520 D. 640

Answer - Option D
Explanation - 16 = [latex]P \times {( \frac {5}{100})}^{2}[/latex]
P = 6400
SI = [latex]\frac {(6400 \times 5*2)}{100} [/latex]=640
2. The difference between the SI and CI on Rs.5000 at 10% per annum for 2 year is

A. 24 B. 35 C. 50 D. 56

Answer - Option C
Explanation - d = [latex]p {(\frac {r}{100})}^{2}[/latex]
= [latex]5000 {(\frac {10}{100})}^{2}[/latex]
d = 50

1. The cash difference between the selling price of an article at a profit of 8% and 4% is Rs 3 the ratio of the two selling price is

A. 51 : 52 B. 27 : 26 C. 51 : 53 D. 52 : 55

Answer - Option B
Explanation - Let the C.P of the article be Rs. x
Then required ratio = 108% of x / 104% of x
= [latex]\frac {108}{104}[/latex] = 27:26
2. A man sells two flats at the rate of Rs. 2 lakhs each. On one he gains 3% and on the other, he loses 3%. His gain or loss % in the whole transaction is

A. 9% loss B. 2% loss C. 3% loss D. 25% loss

Answer - Option A
Explanation - Loss% = [latex]\frac {{X}^{2}}{100} = \frac {{(3)}^{2}}{100}[/latex] % =0.09%

1. A, B and C can all together do piece of work in 10 days, in which B takes three times as long as A and C together do the work and C takes twice as long as A and B together take to do the work. In how many days B can alone do the work?

A. 35 days B. 33 days C. 43 days D. 40 days

Answer - Option d
Explanation - (A+C) in x days so B completes in 3x days
Then [latex](\frac {1}{x}) + (\frac {1}{3x}) = \frac {1}{10} [/latex]
Solve, x = [latex] \frac {40}{3}[/latex]
So B in 3x = [latex] 3 \times (\frac {40}{3})[/latex] = 40 days
OR
Given A+B+C = 10 and that B takes 3 times as A+C, so A+C is three times stronger than B
So this means that 4 times stronger can do work in 10 days
So 1 time stronger(B) in [latex]4 \times 10[/latex] = 40 days
2. 20 men can complete a piece of work in 14 days. 7 men started the work and after 20 days, 7 more men joined the work. In how many days the remaining work will be completed?

A. 18 days B. 20 days C. 8 days D. 10 days

Answer - Option D
Explanation - Let (7+7) complete remaining work in x days. So
[latex] 20 \times 14 = 7 \times 20 + 14 \times x[/latex]
x = 10 days