Tabular Graph
Directions (1 - 5): Expenditures of a Company (in Lakh Rupees) per Annum Over the given Years.
| Year |
Item of Expenditure |
| Salary |
Fuel and Transport |
Bonus |
Interest on Loans |
Taxes |
| 1998 |
288 |
98 |
3.00 |
23.4 |
83 |
| 1999 |
342 |
112 |
2.52 |
32.5 |
108 |
| 2000 |
324 |
101 |
3.84 |
41.6 |
74 |
| 2001 |
336 |
133 |
3.68 |
36.4 |
88 |
| 2002 |
420 |
142 |
3.96 |
49.4 |
98 |
1. What is the average amount of interest per year which the company had to pay during this period?
A. Rs. 32.43 lakhs
B. Rs. 33.72 lakhs
C. Rs. 34.18 lakhs
D. Rs. 36.66 lakhs
Answer: Option (D)
Explanation:
An average amount of interest paid by the Company during the given period
= Rs. ([latex]\frac{23.4 + 32.5 + 41.6 + 36.4 + 49.4}{5}[/latex]) lakhs
= Rs. ([latex]\frac{183.3}{5}[/latex]) lakhs
= Rs. 36.66 lakhs.
2. The total amount of bonus paid by the company during the given period is approximately what percent of the total amount of salary paid during this period?
A. 0.1%
B. 0.5%
C. 1%
D. 1.25%
Answer: Option (C)
Explanation:
Required percentage
= ([latex]\frac{(3.00 + 2.52 + 3.84 + 3.68 + 3.96)}{(288 + 342 + 324 + 336 + 420)}[/latex]x 100) %
= ([latex]\frac{17}{1710}[/latex] x 100) %
≈ 1%.
3. Total expenditure on all these items in 1998 was approximately what percent of the total expenditure in 2002?
A. 62%
B. 66%
C. 69%
D. 71%
Answer: Option (C)
Explanation:
Required percentage
= ([latex]\frac{(288 + 98 + 3.00 + 23.4 + 83)}{(420 + 142 + 3.96 + 49.4 + 98)}[/latex]x 100) %
= ([latex]\frac{495.4}{713.36}[/latex]x 100)%
≈ 69.45%.
4. The total expenditure of the company over these items during the year 2000 is?
A. Rs. 544.44 lakhs
B. Rs. 501.11 lakhs
C. Rs. 446.46 lakhs
D. Rs. 478.87 lakhs
Answer: Option (A)
Explanation:
The total expenditure of the Company during 2000
= Rs. (324 + 101 + 3.84 + 41.6 + 74) lakhs
= Rs. 544.44 lakhs.
5. The ratio between the total expenditure on Taxes for all the years and the total expenditure on Fuel and Transport for all the years respectively is approximate?
A. 4:7
B. 10:13
C. 15:18
D. 5:8
Answer: Option (B)
Explanation:
Required ratio
= ([latex]\frac{(83 + 108 + 74 + 88 + 98)}{(98 + 112 + 101 + 133 + 142)}[/latex])
= ([latex]\frac{451}{586}[/latex])
= [latex]\frac{1}{1.3}[/latex]
= [latex]\frac{10}{13}[/latex].
Line Graph
1. What is the difference between the number of vehicles manufactured by Company Y in 2000 and 2001?
A. 50000
B. 42000
C. 33000
D. 21000
Answer: Option (D)
Explanation:
Required difference = (128000 - 107000) = 21000.
2. What is the difference between the total productions of the two Companies in the given years?
A. 19000
B. 22000
C. 26000
D. 28000
Answer: Option (C)
Explanation:
From the line graph, it is clear that the productions of Company X in the years 1997, 1998, 1999, 2000, 2001 and 2002 are 119000, 99000, 141000, 78000, 120000 and 159000 and those of Company Y is 139000, 120000,100000, 128000, 107000 and 148000 respectively.
Total production of Company X from 1997 to 2002
= 119000 + 99000 + 141000 + 78000 + 120000 + 159000
= 716000.
and total production of Company Y from 1997 to 2002
= 139000 + 120000 + 100000 + 128000 + 107000 + 148000
= 742000.
Difference = (742000 - 716000) = 26000.
3. What are the average numbers of vehicles manufactured by Company X over the given period? (rounded off to the nearest integer)
A. 119333
B. 113666
C. 112778
D. 111223
Answer: Option (A)
Explanation:
Average number of vehicles manufactured by Company X
=[latex]\frac{1}{6}[/latex] x (119000 + 99000 + 141000 + 78000 + 120000 + 159000)
= 119333.
4. In which of the following years, the difference between the productions of Companies X and Y was the maximum among the given years?
A. 1997
B. 1998
C. 1999
D. 2000
Answer: Option (D)
Explanation:
The difference between the productions of Companies X and Y in various years are:
For 1997 (139000 - 119000) = 20000.
For 1998 (120000 - 99000) = 21000.
For 1999 (141000 - 100000) = 41000.
For 2000 (128000 - 78000) = 50000.
For 2001 (120000 - 107000) = 13000.
For 2002 (159000 - 148000) = 11000.
Clearly, the maximum difference was in 2000.
5. The production of Company Y in 2000 was approximately what percent of the production of Company X in the same year?
A. 173
B. 164
C. 132
D. 97
Answer: Option (B)
Explanation:
Required percentage =([latex]\frac{128000}{78000}[/latex]x 100 )% = 164%.
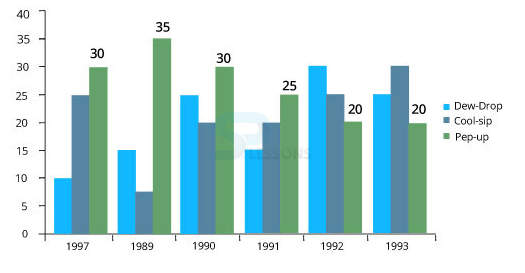
Bar Graph
1. In which year was the sale of 'Pep-up' the maximum?
A. 1990
B. 1991
C. 1992
D. 1993
E. None of these
Answer: Option (E)
Explanation:
Sale of Pep-up was the maximum in the year 1989.
2. In the case of which soft drink was the average annual sale maximum in the given period?
A. Pep-up only
B. Cool-sip only
C. Dew-drop only
D. Cool-sip and Dew-drop
E. Pep-up and Dew-drop
Answer: Option (A)
Explanation:
Average annual sale of Dew-drop = (10 + 15 + 25 + 15 + 30 + 25)/6 = 20 lakhs
Average annual sale of Cool-sip = (25 + 7 + 20 + 20 + 25 + 30)/6 = 21.16 lakhs
Average annual sale of Pep-up = (30 + 35 + 30 + 25 + 20 + 20)/6 = 26.66 lakhs.
3. In the case of cool-sip drink, what was the approximate percent increase in sale in 1992 over its sale in 1991?
A. Less than 20
B. 20-25
C. 25
D. 31-35 E. 36-40
Answer: Option (C)
Explanation:
Required % = (25 - 20)/20 * 100 = 25%.
4. In the year 1990, what was the difference between the number of 'Pep-up' and 'Cool-sip' bottles sold?
A. 50,00,000
B. 5,00,000
C. 50,000
D. 5,000
E. 10,00,000
Answer: Option (E)
Explanation:
Required number = 30 - 20 = 10,00,000.
5. What was the approximate percent drop in the sale of Pep-up in 1990 over its sale in 1989?
A. 5
B. 12
C. 14
D. 20
E. 28
Answer: Option (C)
Explanation:
Required % drop = (35 - 30)/35 * 100 ≈ 14%.
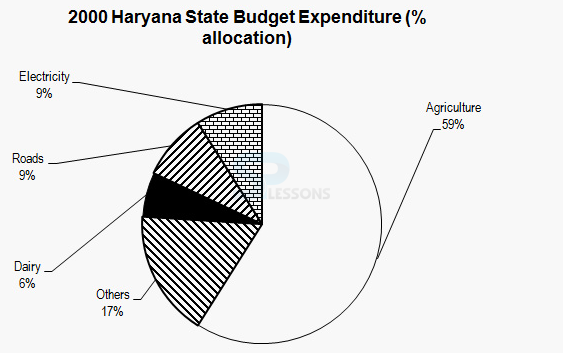
Pie Graph
Direction (1-5): Go through the following pie chart and answer the questions given below that.
1. Approximately how many degrees should be there in the central angle of the sector for agriculture expenditure?
A. 220
B. 213
C. 210
D. 208
Answer: Option (B)
Explanation:
In the pie chart, 100% is spread over 360°. Therefore 1 % = 3.6°. Agriculture expenditure = 59 %. Therefore 3.6 59 = 212.4°.
2. Approximately what is the ratio of expenditure on agriculture to that on dairy?
A. 8:3
B. 9:2
C. 70:1
D. 10:1
Answer: Option (D)
Explanation:
Over here, one common mistake is that students calculate the actual values of agriculture and dairy. Since budget expenditure is proportional to % of the area covered, the ratio of agriculture to dairy expenditure would be the ratio of corresponding % allocations. Therefore, Agriculture/Dairy = 59/6 = 10/1.
3. In Haryana, in 2000, a total expenditure of Rs. 120mn was incurred. Approximately how many millions did the Haryana government spend on roads?
A. 15.4
B. 20
C. 10.8
D. 12
Answer: Option (C)
Explanation:
Total expenditure = 100% = Rs. 120 mn. Expenditure on roads = 9% = 9/100 × 120 = Rs. 10.8mn.
4. If Rs. 9mn was spent in 2000 on Dairy, what would have been the total expenses in that year in million?
A. 150
B. 140
C. 160
D. 130
Answer: Option (A)
Explanation:
9mn were spent on dairy. This amount represents 6% of total expenditure in the year 2000.
6 = (Dairy expenditure/Total expenditure ) × 100
6 = (9/Total expenditure ) × 100
Total Exp = 100 × (9/6) = Rs. 150mn.
5. In 1999, Haryana spent 11% of all its expenses on Roads. “Did Haryana spend more on Roads expenditure in 1999 than in 2000?” To answer the question, we
A. Do not require any additional data.
B. Require to know the total amount spent in each year.
C. Require the exact %age break-up of the various items of expenses in 1999.
D. Require the expenditure on dairy in both the years.
Answer: Option (B)
Explanation:
% gives us just a proportional indication of total quantity.
Unless total expenditure is known, % of that is meaningless.
Hence, to compare expenditure on roads in 1999 and 2000, the total amount spent must be known.
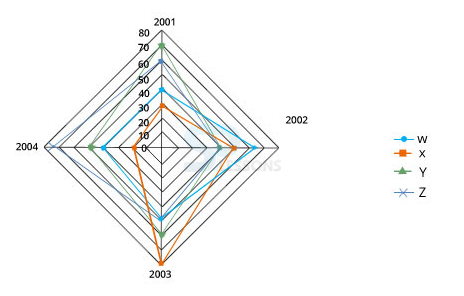
Radar Graph Caselet
Direction (1-5): The following web graph shows the share price of the four companies W, X, Y, and Z in 2001, 2002, 2003, and 2004 respectively. Study the graph and answer the questions below:
1. Which share shows the maximum percentage change in value in 2004 over its value in 2001 of the company?
Answer: Option (B)
2. In which year is the average share price of the four companies the lowest?
A. 2001
B. 2002
C. 2003
D. 2004
Answer: Option (D)
3. Which share shows the highest percentage change in value over any two consecutive months?
Answer: Option (B)
4. Shyam decided to buy 80 shares of all the companies in 2001, 100 of each company in 2002, and 50 of each in 2003. What will be Shyam’s profit/loss if sold all these shares in 2004?
A. Loss of Rs. 4950
B. Profit of Rs. 500
C. Loss of Rs. 4800
D. Profit of Rs 4060
Answer: Option (A)
5. In which year is the average share price of the four companies the highest?
A. 2001
B. 2002
C. 2003
D. 2004
Answer: Option (B)
Missing Case DI
Directions (1-5):Given below is the table showing income, expenditure and profit percentage of company A from 2011-2016.
| States |
LEDs distributed(in lakh) |
High income people |
Middle income people |
Low income people |
| Uttrakhand |
6.5 |
15% |
— |
50% |
| Bihar |
3.4 |
12% |
32% |
— |
| U.P. |
2.5 |
8% |
13% |
— |
| Haryana |
5.2 |
— |
25% |
— |
| Punjab |
— |
21% |
22% |
— |
| Assam |
4.2 |
— |
9% |
78% |
| Kerala |
4.7 |
15% |
— |
60% |
Note: some values are missing, you have to find these values as per given data only.
1. Total distribution of LEDs in Uttrakhand is what % more/less than that of total distribution of LEDs in Assam and Punjab together?
A. 15.58 % less
B. 12.98 % more
C. 18.42 %less
D. 17.23 % more
E. None of these
Answer: Option (D)
2. What is the ratio of distribution of LEDs in low-income people of Bihar to the middle-income people of Kerala?
A. 25:18
B.17:29
C. 19:12
D. 18: 25
E. None of these
Answer: Option (C)
3. What is the difference between the LED’s distribution in High-income people of UP, Uttrakhand, and Kerala together to the LED’s distribution in Middle-income people of Haryana, Punjab and Kerala together?
A. 144800
B. 136500
C. 140900
D. 144200
E. None of these
Answer: Option (C)
4. In Haryana state the ratio of % distribution of LED’s in High-income people to the Low-income people is 2 : 3, then the distribution of LED’s in high-income people in the same state is how much more than that of in middle-income people?
A. 26000
B. 14000
C. 21000
D. 24000
E. None of these
Answer: Option (B)
5. Total distribution of LEDs in low-income people of all the state together excluding Haryana is approximately what % of the total distribution of LEDs in all states together?
A. 63.7%
B. 45.6%
C. 54.9%
D. 50.7%
E. 58.3%
Answer: Option (B)
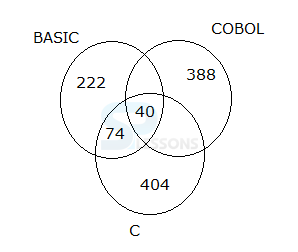
Let it Case DI
Direction (1 - 5): Read the following information and answers the given questions.
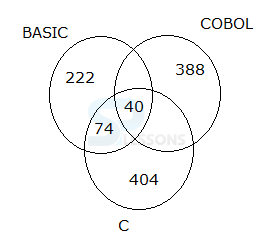
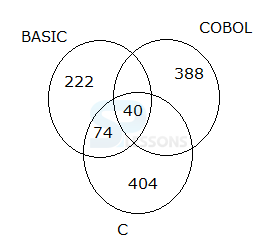
In a college, three programming languages are taught. Out of 1200 students, each one is required to study at least one of the three languages which are BASIC, COBAL and C. 40 students study all the three languages. 404 students study only C, 222 students study only BASIC, 500 students study COBAL, 114 students study both C and BASIC and 388 students study only COBAL.
1. How many students study two programming languages only such that at least one of the two languages is COBAL?
A. 36
B. 72
C. 48
D. 60
E. 80
Answer: Option (B)
Explanation:
Only two languages (One is COBOL)= 1200- (404+388+222+40+74)= 72
2. What is the number of students who study exactly two languages?
A. 146
B. 126
C. 136
D. 156
E. 132
Answer: Option (A)
Explanation:
COBOL+BASIC and COBOL+C = 1200- (404+388+222+40+74)= 72
Exactly any two languages only = = 72+74 = 146
3. If the number of students study C language is 554, then what is the number of students study BASIC language?
A. 348
B. 372
C. 336
D. 308
E. 318
Answer: Option (B)
Explanation:
COBOL+BASIC and COBOL+C = 1200- (404+388+222+40+74)= 72
C language= 404+74+40+(72-COBOL language and BASIC only)=554
Therefore, COBOL+BASIC =( 404+74+40+72)-554=36
Required total = 222+74+40+36 = 372
4. If the number of students study BASIC language is 384, then what is the number of students study both COBOL and C languages?
A. 24
B. 36
C. 72
D. 48
E. 64
Answer: Option (E)
Explanation:
BASIC language = 222+74+40+(BASIC and COBOL only)=384
BASIC and COBOL only=384-(222+74+40)=48
Therefore, COBOL and C only=72(BASIC and COBOL only + COBOL and C only) – 48=24
Both COBOL and C = 40+24=64
5. What is the total number of students study C and BASIC languages?
A. 720
B. 772
C. 812
D. 782
E. 834
Answer: Option (C)
Explanation:
Number of students study C and BASIC language = Total-COBOL only
=1200-388=812.
Data Sufficiency
Direction (1-5): each of the questions below consists of a question and two statements numbered I and II given below it. You have to decide whether the data provided in the statements are sufficient to answer the question. Read both the statements and
Give answer:
(A) If the data in statement I alone are sufficient to answer the question, while the data in statement II alone are not sufficient to answer the question
(B) If the data in statement II alone are sufficient to answer the question, while the data in statement I alone are not sufficient to answer the question
(C) If the data either in statement I alone or in statement II alone are sufficient to answer the question
(D) If the data given in both statements I and II together are not sufficient to answer the question and
(E) If the data in both statements I and II together are necessary to answer the question.
1. How is T related to K?
Statements:
i. K has two sons; one of the sons is A.
ii. The mother of T has only two sons - Aand B.
A. I alone is sufficient while II alone is not sufficient
B. II alone is sufficient while I alone is not sufficient
C. Either I or II is sufficient
D. Neither I nor II is sufficient
E. Both I and II are sufficient
Answer: Option (E)
Explanation:
From II, we know that T's mother has only two sons, A and B. This implies that T is the sister of both A and B. But, from I, A is also K's son. So, T is the daughter of K.
2. What is the shortest distance between Devipur and Durgapur?
Statements:
i. Durgapur is 20 kms away from Rampur.
ii. Devipur is 15 kms away from Rampur.
A. I alone is sufficient while II alone is not sufficient
B. II alone is sufficient while I alone is not sufficient
C. Either I or II is sufficient
D. Neither I nor II is sufficient
E. Both I and II are sufficient
Answer: Option (D)
Explanation:
Clearly, the distance of each village from Rampur is given in I and II. But nothing about their relative positions is mentioned. So, the distance between the two villages cannot be calculated.
3. How is A related to D?
Statements:
i. B is the brother of A.
ii. B is D's son.
A. I alone is sufficient while II alone is not sufficient
B. II alone is sufficient while I alone is not sufficient
C. Either I or II is sufficient
D. Neither I nor II is sufficient
E. Both I and II are sufficient
Answer: Option (D)
Explanation:
From I and II, we conclude that A is either son or daughter of D.
4. Manoj, Prabhakar, Akash and Kamal are four friends. Who among them is the heaviest?
Statements:
i. Prabhakar is heavier than Manoj and Kamal but lighter than Akash.
ii. Manoj is lighter than Prabhakar and Akash but heavier than Kamal.
A. I alone is sufficient while II alone is not sufficient
B. II alone is sufficient while I alone is not sufficient
C. Either I or II is sufficient
D. Neither I nor II is sufficient
E. Both I and II are sufficient
Answer: Option (A)
Explanation:
From I, we have: P > M, P > K, A > P.
Thus, A > P > M > K or A > P > K > M. So, Akash is the heaviest.
From II, we have: P > M, A > M, M > K.
Thus, A > P > M > K or P > A > M > K. So, either Akash or Prabhakar is the heaviest.
5. Vinod's and Javed's salaries are in the proportion of 4 : 3 respectively. What is Vinod's salary?
Statements:
i. Javed's salary is 75% that of Vinod's salary.
ii. Javed's salary is Rs 4500.
A. I alone is sufficient while II alone is not sufficient
B. II alone is sufficient while I alone is not sufficient
C. Either I or II is sufficient
D. Neither I nor II is sufficient
E. Both I and II are sufficient
Answer: Option (B)
Explanation:
Statement I is merely an interpretation of the information contained in the question.
However, Vinod's salary can be ascertained from II as follows : Let Vinod's and Javed's salaries be 4x and 3x respectively. Then, 3x = 4500 or x = 1500. Therefore Vinod's salary = 4x = Rs. 6000.
Probability
1. If a dice is thrown twice, what is the probability of not getting a one on either throw?
A. 1/12
B. 1/18
C. 25/36
D 12/36
Answer: Option (C)
Explanation:
Out of total 36 possible outcomes, getting 1 on either draw can happen in = 11 ways
Reqd. Probability = 1 – (Probability of Getting one on either draw) = 1 - 11 / 36 = 25 / 36.
2. Two cards are drawn in succession from a pack of 52 cards, without replacement. What is the probability, that the first is a Queen and the second is a Jack of a different suit?
A. 1/52
B. 1/13
C. 4/13
D. 1/221
Answer: Option (D)
Explanation:
The probability of first Queen = 4 / 52
The probability of Second Jack of different suit = 3 / 51
Reqd. Probability = (4/52) x (3/51) = (1/13) x (1/17) = (1/221).
3. Two dice are thrown, what is the probability that both the dices are not having the same number.
A. 1/4
B. 5/6
C. 1/9
D. 1/12
Answer: Option (B)
Explanation:
Total possible outcomes = 36. Favorable outcomes of having same number = 6 [(1, 1) (2, 2) (3, 3) (4, 4) (5, 5) (6, 6)].
Probability of both the dices having same number = 6 / 36 = 1 / 6
Required probability = 1 - 1 / 6 = 5 / 6.
4. Determine the probability that a number chosen at random from the digits 1, 2, 3, ……., 10 will be a multiple of
A. 1/4
B. 1/3
C. 1/5
D. 1/2
Answer: Option (C)
Explanation:
Total possible outcomes = 10. Favorable outcomes = 2. (i.e. 4,8).
Probability = 2 / 10 = 1 / 5.
5. A dice is thrown, what is the probability that the number obtained is a prime number.
A. 1/6
B. 1/8
C. 1/2
D. 1/3
Answer: Option (C)
Explanation:
Dice is thrown, the total possible outcomes = 6.
Favorable outcomes = 3 i.e. (2,3,5). Probability = 3 / 6 = 1 / 2.
Permutation & Combination
Directions (1-5): Solve the following combination and permutation questions as per the best of your abilities. You may have to apply combination and permutation formula to answer some of these questions.
1. Find the sum of all the 4 digit numbers that can be formed with the digits 3, 4, 5 and 6.
A. 119988
B. 11988
C. 191988
D. None of these
Answer: Option (A)
Explanation:
No. of Digits = 4 All are distinct; They can be arranged in 4! = 24 ways
Each of the digits 3, 4, 5 and 6 occur at unit place = 3! Ways = 6 ways.
Thus there will be 6 numbers ending with 3, 4, 5 and 6 each. So the sum of the digits at unit's place = 6(3 + 4 + 5 + 6) =108
The sum of numbers = 108 × 10[latex]^{3}[/latex] + 108 × 10[latex]^{2}[/latex] + 108 × 10[latex]^{1}[/latex] + 108 × 10[latex]^{0}[/latex] = 119988.
2. Find the sum of all the 4 digit numbers that can be formed with the digits 3, 4, 4 and 2.
A. 43339
B. 43999
C. 43329
D. None of these
Answer: Option (C)
Explanation:
Here each of the digits 2 and 3 will occur at unit, tens, hundred and thousand place ([latex]^3p_{3}[/latex] /2!) = 3 times. Digit 4 will occur at each place = 6 times;
∴ Sum of digits at unit, tens, hundred and thousand place = 3 × 3 + 6 × 4 + 3 × 2 =39. Sum of numbers formed =
= 39 × 10[latex]^{3}[/latex] + 39× 10[latex]^{2}[/latex] + 39 × 10[latex]^{1}[/latex] + 39 × 10[latex]^{0}[/latex]= 43329.
4. The number of straight lines that can be drawn out of 12 points of which 8 are collinear is
Answer: Option (A)
Explanation:
The required number of lines= [latex]^12C_{2}[/latex] – [latex]^8C_{2}[/latex] + 1 = 1 + 66 – 28 = 39.
5. In how many ways can you rearrange the word JUMBLE such that the rearranged word starts with a vowel?
A. 120
B. 240
C. 360
D. 60
Answer: Option (B)
Explanation:
JUMBLE is a six-lettered word. Since the rearranged word has to start with a vowel, the first letter can be either U or E. The balance 5 letters can be arranged in [latex]^5P_{5}[/latex] or 5! ways. Total number of words = 2 × 5! = 240.
 Introduction
Introduction  Pattern
Pattern  Syllabus
Syllabus  Samples
Samples