Prepositions
1. The public are cautioned---- pickpockets.

A. against B. to C. at D. by

Answer: Option A
2."Will you walk — my parlor?" said the spider — the fly.

A. into, to B. by, with C. to, is D. at, to

Answer: Option A
3. We suffered — your neglect.

A. to B. since C. at D. from

Answer: Option D
Active Voice and Passive Voice
1. My bicycle has been sold.

A. I had sold my bicycle. B. I have sold my bicycle. C. They sold my bicycle. D. My bicycle will sell.

Answer: Option B
2. He kept me waiting.

A. He asked me to keep waiting. B. I was kept waiting. C. He asked me to wait and did not return. D. I was waiting for him.

Answer: Option B
3. May you be blessed with happiness.

A. I bless you with happiness. B. May God bless you with happiness. C. God blesses you with happiness. D. God will bless you with happiness.

Answer: Option B
Joining Sentences.
1. He is, no doubt, very clever. He will fall into my trap. (A) Although he is clever..... (B) If he is clever, he will fall..... (C) In spite of being clever he.....

A. A and B B. Only A C. A and C D. Only C E. All the three

Answer: Option C
Explanation: The two sentences express contradictory ideas. Hence conjunctions like 'though' can combine the sentences meaningfully. 'Despite being ... or In spite of being' ... can also be used to express the same idea.
2. He is too headstrong. He will not listen to advise. (A) Unless he is too headstrong..... (B) If he is too headstrong..... (C) He is so headstrong that.....

A. Only A B. A and C C. B and C D. A and B E. B and C

Answer: Option E
Explanation: Both the sentences talk about the same person. One qualifies the other. The conjunctions 'so ... that' and 'too ... to' can be used to combine the given sentences meaningfully. But B begins with 'if' and hence is incorrect.
3. They will not win the match. It is certain. (A) It is certain that they ..... (B) Although it is certain ..... (C) Unless they win the match .....

A. Only A B. Only B C. Only C D. A and B E. None of these

Answer: Option A
Explanation: The second sentence ascertains or affirms the first statement. Hence starter A, which uses 'that', is the best way of combining these sentences. The use of 'although' or 'unless' distorts the meaning.
Spotting Errors
1. He took to (a) / reading Times (b) / for better knowledge (c) / of the facts (d) / No error (e)

A. he took to B. reading times C. for better knowledge D. of the facts E. no error

Answer: Option B
2. This town isn’t very well known (a) / and there isn’t much to see (b) / so a few tourists come here (c) / No error (d)

A. this town isn’t very well known B. and there isn’t much to see C. so a few tourists come here D. no error

Answer: Option C
3. Suganya opened a almirah (a) / full of books (b) / and took one of them (c) / for reading (d) / No error (e)

A. suganya opened a almirah B. full of books C. and took one of them D. for reading E. no error

Answer: Option A
Synonyms
1. Kin

A. Exult B. Twist C. Friend D. Relative

Answer: Option D
Explanation: Kin means people with common ancestors, or relatives
2. Predict

A. Foretell B. Decide C. Prevent D. Discover

Answer: Option A
Explanation: To predict means to declare in advance or to foretell.
3. Gracious

A. Pretty B. Clever C. Pleasant D. Present

Answer: Option C
Explanation: Gracious means to be pleasant or considerate in social interactions.
Sentence Improvement
1. Where politics fails, economics may sometimes succeed.

A. may sometimes succeed B. may sometime succeed C. sometimes succeed D. sometimes succeeds

Answer: Option D
2. Only three-fourths of the work is complete.

A. has complete B. have complete C. is complete D. had complete

Answer: Option C
3. It is better to say too little than too much.

A. only little B. very little C. little D. none

Answer: Option C
Error Correction (Phrase in colour).
1. The organization aims to providing with satellite-based data on climate-relevant information with highest possible levels of accuracy and reliability.

A. to provide with B. at providing with C. to provide D. to the provision of E. No correction required

Answer: Option C
Explanation: The organization aims 'at providing' or 'to provide' something. The use of 'with' is incorrect. It aims 'to provide' something not 'provide with something'.
2. Mobile phones are now-a-days used not just to make calls or send and receive text messages but to also carry on financial transactions.

A. but also to carry on B. but to carry out also C. but also to carry out D. and to carry out E. No correction required

Answer: Option C
Explanation: They are used 'not only to make calls but also to carry out'. The use of'to before also' is ungrammatical. Also, financial transactions are 'carried out'. 'carry on' is inept in this context. The correction is 'but also to carry out'.
3. Scientists have estimated that millions of creatures living in water had been dying every year if they become entangled in plastic pollution or ingest it.

A. every year is dying as B. has died every year as if C. die every year when D. was dying every year when E. No correction required.

Answer: Option C
Explanation: Scientists say that it happens 'every year'. Hence it is most apt to use the simple present tense (die) in this context. Also the use of 'if' as the conjunction is illogical. They die 'when they become entangled in'.
Para Completion
Directions (1-3): All the following paragraphs have given five options, select the best alternatives that fit in the blank of a paragraph in a most appropriate manner and given a meaningful sentence to the entire paragraph.
Q1. In the beginning, there was no real stock market. However, stock exchanges did take place in smaller groups and corporations. This all took place during the 1700s where stocks were already around for a long time before________

A. That but it wasn't really popular in the United States. B. That but Stocks originally started as auctions where traders called out names of companies and the shares available. C. That there was an auction that took place and the shares went to the highest bidders. D. Both a and b E. Both b and c

Answer: Option A
Q2. After the American Revolution which took place between 1775 to 1783 the number of securities increased dramatically. The number of shares being bought grew so large that brokers had to organize in order to handle the growing volume. During the 2nd half of the 19th century, New York City became ________

A. After that, the New York Stock Exchange became the number one trading center. B. The reason for this being that its members focused on buying securities of larger corporations. C. The central financial center of the United States. D. Both a and b E. Both b and c

Answer: Option C
Q3. At that time all the smaller stocks of smaller companies were handled on the streets of downtown New York City. In 1908 these brokers formed the New York Curb Agency which is now known as __________

A. During the 1920's millions of Americans began investing in stocks for the first time. B. They heard about how rich people were getting by investing so they all decided to do it. C. Many new investors entered the stock market using borrowed money. D. The American Stock Exchange. It was renamed to this in 1953. E. Both a and b

Answer: Option D
Sentence Completion
1. Civility can flourish, but only if the upcoming generation ______________________________

A. wants to do it. B. take some action. C. decides to spread that quality around. D. behave properly.

Answer: Option C
2. When it comes to success, a majority of people assume that making it to the top __________________

A. needs hard work and maturity. B. requires ethical compromises. C. demands over time. D. Requires good business knowledge.

Answer: Option B
3. The question isn’t who is going to let me, it’s who’s going to _______________.

A. work with me. B. ask me not to do. C. stop me. D. judge me.

Answer: Option C
Fill in the blanks
1. The National Knowledge Commission has said that India will have to bring ____ in education if it has to emerge as the most ____ workforce of the world.

A. changes, biggest B. reforms, talented C. alleviation. Skillful D. quality, brighter E. outcomes demanded

Answer: Option B
2. Norway has stolen a march over other developed countries by ____ that it would reduce 40% of it’s greenhouse gas emissions by 2020 and ____ carbon-neutral by 2030.

A. allowing, turn B. posing, grew C. estimating, exist D. perceiving, arising E. declaring, become

Answer: Option E
3. According to the language experts, children should begin talking in their mother tongue rather than a foreign language which can ____ affect their comprehension abilities leading to serious language based ____ later in their lives.

A. significantly, abilities B. appropriately, achievement C. severely, advantages D. adversely, problems E. positively issued

Answer: Option D
Error Correction (Underlined Part).
1. Have you been more careful, the accident could have been averted?

A. If you have been B. Had you been C. Have you been D. If you could have been E. No correction required

Answer: Option B
Explanation: As the sentence talks about the past it is apt to say. 'Had you been more careful ...'.
2. People attended the meeting in large numbers, despite of the heavy downpour.

A. besides the heavy downpour B. despite the heavy downpour C. in spite of the heavy downpour D. although the heavy downpour E. No correction required

Answer: Option B
Explanation: The preposition 'of' should not be used with 'despite'.
3. The warden did not approve with the student's behavior.

A. approve with that of the student's behavior B. approve of the student's behavior C. approve of the student's behavior D. approve for the student's behavior E. No correction required

Answer: Option B
Explanation: The word 'approve' should be followed by the preposition 'of'.
Passage Completion
In economics, the term recession generally describes the reduction of a country’s Gross Domestic Product (GDP) for at least two quarters. A recession is...( I )...by rising unemployment, an increase in government borrowing,...( II)..., of share and stock prices, and falling investment. All of these characteristics have effects on people. Some recessions have been anticipated by stock market declines. The real estate market also usually...( III )...before a recession.
1. Choose the best word in place of ( I ) from the given passage

A. imagined B. depict C. shown D. visualized E. characterized

Answer: Option E
2. Choose the best word in place of ( II ) from the given passage

A. Increase B. variance C. more D. decrease E. abundance

Answer: Option D
3. Choose the best word in place of ( III ) from the given passage

A. weakens B. initiates C. awakens D. strengthens E. volatile

Answer: Option A
Substitution.
1. The plants and vegetation of a certain region.

A. flora B. fauna C. forest D. vegetation

Answer: Option A
2. The art of beautiful handwriting.

A. painter B. calligraphy C. palegraphy D. draftsman

Answer: Option B
3. One whose wife is dead.

A. widow B. celibate C. widower D. divorcee

Answer: Option C
Idioms and Phrases.
1. She exhibited remarkable sang froid during the crisis.

A. composure B. temper C. anger D. irritation

Answer: Option A
2. Mrs Rashmi has been in the blues for the last several weeks.

A. unwell B. abroad C. lonely D. depressed

Answer: Option D
3. None of this hanky panky, please talk straight.

A. jugglery B. indifference C. diversification D. obsession

Answer: Option A
Antonyms
1. Luminous

A. Clear B. Dim C. Brittle D. Clever

Answer: Option B
Explanation: Luminous means radiating or reflecting light, or glowing; Dim means dark or dull
2. Pit

A. Group B. Peak C. Select D. Marry

Answer: Option B
Explanation: A pit is a hole and a Peak is the top of a hill or mountain
3. Rotund

A. Round B. Unimportant C. Thin D. Dull

Answer: Option C
Explanation: Rotund means rounded or plump, therefore Thin is the opposite
Sentence Arrangement
1. All religions are (P) to advance the cause of peace (Q) in a holy partnership (R) justice and freedom (S) bound together

A. PQRS B. PRQS C. SPQR D. SQPR

Answer: Option D
2. As lightning accompanies thunder (P) was mingled with (Q) so in my character (R) the mutterings of my wrath (S) a flash of humour

A. QSPR B. PRSQ C. QPRS D. QRPS

Answer: Option A
3. The boy (P) with big blue eyes (Q) watched him (R) and he never said a word (S) that had an uncanny cold fire in them

A. PQRS B. PQSR C. QPSR D. QRPS

Answer: Option C

Inserting Correct Mathematical Sign
1. If ‘x’ means ‘-' , ‘-' means ‘x’, ‘+’ means ‘÷' and ‘÷' means ‘-', then (15 - 10) ÷ (130 + 10) x 50 = ?

A. 1800 B. 113 C. 2000 D. 87

Answer: Option D
2. Substitute the arithmetical signs in the place of * in the following equation : 7 * 7 * 2 * 1 = 12

A. x - ÷ B. + - x C. x - + D. + x –

Answer: Option B
3. If ‘+’ means ‘÷’, ‘-'means ‘x’, ‘÷’ means ‘+’ and ‘x’ means ‘-'then 36 x 12 + 4 ÷ 6 + 2 – 3 = ?

A. 42 B. 18 C. 40 D. 2

Answer: Option A
Odd Man Out
1. 331, 482, 551, 263, 383, 362, 284

A. 263 B. 383 C. 331 D. 551

Answer: Option B
Explanation: In each number except 383, the product of the first and third digits is the middle one.
2. 41, 43, 47, 53, 61, 71, 73, 81

A. 61 B. 71 C. 73 D. 81

Answer: Option D
Explanation: Each of the numbers except 81 is a prime number.
3. 10, 14, 16, 18, 21, 24, 26

A. 26 B. 24 C. 21 D. 18

Answer: Option C
Explanation: Each of the numbers except 21 is an even number.
Mutual Relation Problem
1. Deepak said to Nitin, "That boy playing with the football is the younger of the two brothers of the daughter of my father's wife." How is the boy playing football related to Deepak?

A. Son B. Brother C. Cousin D. Brother-in-law

Answer: Option B
Explanation: Father's wife → mother. Hence, the daughter of the mother means sister and sister's younger brother means brother. Therefore, the boy is the brother of Deepak.
2. (i) In a family of six persons A, B, C, D, E, and F, there are two married couples. (ii) D is the grandmother of A and mother of B. (iii) C is the wife of B and mother of F. (iv) F is the granddaughter of E. What is C to A?

A. Daughter B. Grandmother C. Mother D. Cannot be determined E. None of these

Answer: Option C
Explanation: C is the wife of B and D is the mother of B. So, C is the grandmother of A. So, C is the mother of A.
3. P + Q means P is the brother of Q; P - Q means P is the mother of Q and P * Q means P is the sister of Q. Which of the following means M is the maternal uncle of R? Option:

A. M + K + R B. M - R + K C. M + K - R D. M + K * R E. None of these

Answer: Option C
Explanation: M is the maternal uncle of R means M is the brother of the mother (say K) of R i.e. M + K - R.
Number Puzzle
1. Which number replaces the question marks?

A. 16 B. 13 C. 97 D. 56

Answer: Option B
Explanation : In each circle, starting at the top left segment, numbers increase, as you move clockwise, by 2 for the upper left circle, 3 for the upper right, 4 for the lower right and 5 for the lower left.
2. Which number replaces the question marks?

A. 9 B. 6 C. 3 D. 1

Answer : Option C
Explanation : In each group of 3 numbers, the lower number equals the average of the top two numbers.
3. Which number replaces the question marks?

A. 2 and 3 B. 8 and 1 C. 9 and 9 D. 5 and 6

Answer: Option B
Explanation : Reading each row as 3 separate 2-digit numbers, the central number equals the average of the left and right-hand numbers.
Human Relation
1. X told Y, “Though I am the son of your father, you are not my brother”. How is X related to Y?

A. Sister B. Son C. Daughter D. Father E. None of these

Answer: Option A
2. Introducing Rajesh, Neha said, his brother’s father is the only son of my grandfather. How is Neha related to Rajesh?

A. Daughter B. Sister C. Mother D. Niece E. None of these

Answer: Option B
3. Lakshmi and Meena were Rohan’s wives. Shalini is Meena’s step-daughter. How was Lakshmi related to Shalini?

A. Sister B. Mother-in-law C. Mother D. Step-daughter E. None of these

Answer: Option C
Non-Verbal Reasoning
1. Choose the box that is similar to the box formed from the given sheet of paper (X).

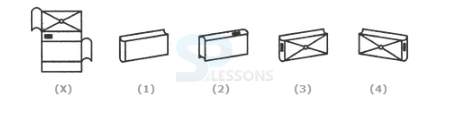
A. 1 and 4 only B. 3 and 4 only C. 1 and 2 only D. 2 and 3 only

Answer: Option A
Explanation: The fig. (X) is similar to the Form I. So when the sheet shown in fig. (X) is folded to form a cube then one of the two half-shaded faces lies opposite to one of the blank faces and the other half-shaded face lies opposite to another blank face. The two remaining blank faces lie opposite to each other. Thus, both the cubes are shown in figures (1).and (4) can be formed when the sheet shown in fig. (X) is folded. Also, though the cubes shown in figures (2) and (3) have faces that can appear adjacent to each other but the cube formed by folding the sheet in fig. (X) cannot be rotated to form either of the two. Hence, the cubes in figures (2) and (3) cannot be formed.
2. Choose the box that is similar to the box formed from the given sheet of paper (X).

A. 1 only B. 2 only C. 1 and 3 only D. 1, 2, 3 and 4 only

Answer: Option B
Explanation: The fig. (X) is similar to the Form III. So, when the sheet in fig. (X) is folded to form a cube, then 'F' appears opposite 'B', 'E' appears opposite 'C' and 'A' appears opposite 'D' Therefore, the cube in fig. (1) which shows 'F' adjacent to 'B' the cube in fig. (3) which shows 'E' adjacent to 'C' and the cube in fig. (4) which shows 'A' adjacent to 'D' cannot be formed. Hence, only the cube in fig. (2) can be formed.
3. Which of the following finished patterns can be obtained from the piece of cardboard (X) shown below?

A. 1 B. 2 C. 3 D. 4

Answer: Option A
Explanation: The pattern on fig. (X) and also the fact that the faces are a rectangle indicate that only fig. (1) can be obtained by folding fig. (X).
Distance and Direction Sense Test
1. Starting from the point X, Jayant walked 15 m towards west. He turned left and walked 20 m. He then turned left and walked 15 m. After this he turned to his right and walked 12 m. How far and in which directions is now Jayant from X?

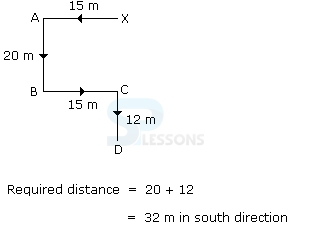
A. 32 m, South B. 47 m, East C. 42 m, North D. 27 m, South

Answer: Option A
Explanation:

2. Two cars start from the opposite places of the main road, 150 km apart. The first car runs for 25 km and takes a right turn and then runs 15 km. It then turns left and then runs for another 25 km and then takes the direction back to reach the main road. In the meantime, due to minor break down the other car has run only 35 km along the main road. What would be the distance between two cars at this point?

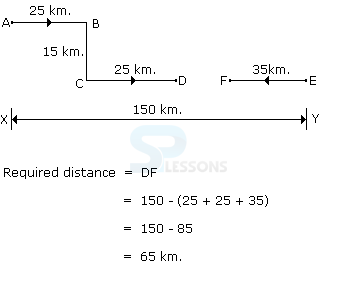
A. 65 km B. 75 km C. 80 km D. 85 km

Answer: Option A
Explanation:

3. A boy rode his bicycle Northward, then turned left and rode 1 km and again turned left and rode 2 km. He found himself 1 km west of his starting point. How far did he ride northward initially?

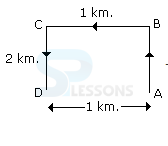
A. 1 km B. 2 km C. 3 km D. 5 km

Answer: Option B
Explanation

Dictionary Words
1. Arrange the following words as per order in the dictionary. 1. Oppose, 2. Opposite, 3. Opposition, 4. Optional, 5. Opportune

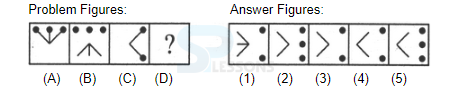
A. 3, 2, 4, 5, 1 B. 5, 4, 1, 3, 2 C. 3, 2, 5, 1, 4 D. 5, 1, 2, 3, 4

Answer: Option D
Explanation In dictionary order, words are placed in alphabetical order on the basis of the first letter in which they differ. Therefore, the order will be: Opportune 5, Oppose 1, Opposite 2, Opposition 3, Optional 4.
2. Which of the given responses would be a dictionary order of the following? 1. Prescription, 2. Prescriber, 3. Prescutum, 4. Prescript

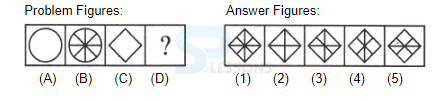
A. 4, 2, 1, 3 B. 2, 4, 1, 3 C. 2, 1, 4, 3 D. 1, 4, 2, 3

Answer: Option B
Solution: The given words can be arranged according to the dictionary order as follows: 2. Prescriber, 4. Prescript, 1. Prescription, 3. Prescutum.
3. Arrange the following words as per order in the dictionary. 1. Silt, 2. Silicon, 3. Silicate, 4. Silken

A. 2, 1, 4, 3 B. 4, 1, 3, 2 C. 3, 2, 4, 1 D. 1, 4, 3, 2

Answer: Option C
Solution: Arranging them in dictionary order 3. Silicate, 2. Silicon, 4. Silken, 1. Silt
Mathematical Operations (Assigning Value to Arithmetic Sign)
1. If Q means 'add to', J means 'multiply by', T means 'subtract from' and K means 'divide by' then 30 K 2 Q 3 J 6 T 5 =?

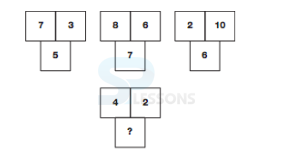
A. 18 B. 28 C. 31 D. 103

Answer: Option B
Explanation: Using Correct Symbols , We have : Given expression = 30 / 2 + 3 x 6 - 5 = 15 + 18 - 5 = 28
2. Select the correct set of symbols which will fit in the given equation is 5 0 3 5 = 20

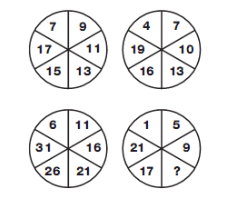
A. x, x, x B. -, +, x C. x, +, x D. +, -, x

Answer: Option B
Explanation: Clearly 5 - 0 + 3 X 5 = 20
3. If × stands for 'addition', ÷ stands for 'subtraction', + stands for 'multiplication' and-stands for 'division', then 20 × 8 ÷ 8 - 4 + 2 = ?

A. 80 B. 25 C. 24 D. 5

Answer: Option C
Explanation: By the Given data , We have the expression: 20 + 8 - 8 ÷ 4 × 2 = 20 + 8 - 2 × 2 = 20 + 8 - 4 = 24.
Analogy
1. Select a suitable figure from the Answer Figures that would replace the question mark (?).

A. 1 B. 2 C. 3 D. 4 E. 5

Answer: Option C
Explanation: Except for the dots, the remaining part of the figure rotates through 180o and shifts to the opposite side of the square boundary.
2. Select a suitable figure from the Answer Figures that would replace the question mark (?).

A. 1 B. 2 C. 3 D. 4 E. 5

Answer: Option A
Explanation: The figure gets divided into eight equal parts.
3. Select a suitable figure from the Answer Figures that would replace the question mark (?).

A. 1 B. 2 C. 3 D. 4 E. 5

Answer: Option E
Explanation: The figure rotates through 90oACW and the arrowhead shifts closer to the black circle.
Numerical Series
1. Identify The Missing Number In The Series. 4, 8, 16, 32,?

A. 48 B. 64 C. 40 D. 46 E. 44

Answer: Option B
Explanation: The numbers double each time
2. Identify The Missing Number In The Series. 4, 3, 5, 9, 12, 17, ?

A. 32 B. 30 C. 33 D. 34 E. 35

Answer: Option D
Explanation: Each number is the sum of the previous and the number 3 places to the left
3. Identify The Missing Number In The Series. 3, 6, 11, 18, ?

A. 30 B. 22 C. 27 D. 29 E. 31

Answer: Option C
Explanation: The interval, beginning with 3, increases by 2 each time.
Tallest, Youngest Relation
1. There are five friends --- Sachin, Kunal, Mohit, Anuj, and Rohan. Sachin is shorter than Kunal but taller than Rohan. Mohit is the tallest. Anuj is a little shorter than Kunal and little taller than Sachin. Who is the shortest?

A. Rohan B. Sachin C. Anuj D. Kunal E. None of these

Answer: Option A
Explanation: Let us denote the five boys by the first letter of their names, namely S, K, M, A, and R. Then, R < S < K < M and S < A < K. R < S < A < K < M. Rohan is the shortest.
2. There are five friends --- Sachin, Kunal, Mohit, Anuj, and Rohan. Sachin is shorter than Kunal but taller than Rohan. Mohit is the tallest. Anuj is a little shorter than Kunal and little taller than Sachin. Who is the second tallest?

A. Sachin B. Kunal C. Anuj D. Rohan E. None of these

Answer: Option B
Explanation: Let us denote the five boys by the first letter of their names, namely S, K, M, A,and R. Then, R < S < K < M and S < A < K. R < S < A < K < M. Kunal is second tallest. There are five friends --- Sachin, Kunal, Mohit, Anuj, and Rohan. Sachin is shorter than Kunal but taller than Rohan. Mohit is the tallest. Anuj is a little shorter than Kunal and little taller than Sachin.
3. If they stand in the order of their heights, who will be in the middle?

A. Kunal B. Rohan C. Sachin D. Anuj E. None of these

Answer: Option D.
Explanation: Let us denote the five boys by the first letter of their names, namely S, K, M, A, and R. Then, R < S < K < M and S < A < K. R < S < A < K < M. Anuj is in the middle.
Number Ranking & Time Sequence Test
1. In a row of boys, If A who is 10th from the left and B who is 9th from the right interchange their positions, A becomes 15th from the left. How many boys are there in the row?

A. 23 B. 31 C. 27 D. 28

Answer: Option A
Explanation: Clearly, A’s new position is 15th from the left. But this is the same as B’s earlier position which is 9th from the right.
2. Sam ranked 9th from the top and 38th from the bottom in a class. How many students are there in the class?

A. 45 B. 47 C. 46 D. 48

Answer: Option C
Explanation: Number of students in class = (8 + 1 + 37) = 46
3. A class of boys stands in a single line, One boy is 19th in order from both the ends, How many boys are there in the class?

A. 37 B. 39 C. 27 D. 38

Answer: Option A
Explanation: Number of boys in the class = (18 + 1 +18) = 37
Coding and Decoding
1. In a certain code, language COMPUTER is written as RFUVQNPC. How will MEDICINE be written in that code language?

A. MFEDJJOE B. EOJDEJFM C. MFEJDJOE D. EOJDJEFM

Answer: Option D
Explanation: There are 8 letters in the word. The code word can be obtained by taking the immediately following letters of the word, expect the first and the last letters of the given word but in the reverse order. That means, in the coded form the first and the last letters have been interchanged while the remaining letters are coded by taking their immediate next letters in the reverse order.
2. If FRIEND is coded as HUMJTK, how is CANDLE written in that code?

A. EDRIRL B. DCQHQK C. ESJFME D. DEQJQM

Answer: Option A
Explanation: The first, second, third, fourth, fifth and sixth letters of the word are respectively moved two, three, four, five, six and seven steps forward to obtain the corresponding letters of the code.
3. If in a code language, COULD is written as BNTKC and MARGIN is written as LZQFHM, how will MOULDING be written in that code?

A. CHMFINTK B. LNKTCHMF C. LNTKCHMF D. NITKHCMF

Answer: Option C
Explanation: Each letter in the word is moved one step backward to obtain the corresponding letter of the code
Assign Artificial Values to Mathematical Digit
1. If + means x, ÷ means –, x means ÷ and means +, then— 5 + 12 ÷ 7 – 44 x 2 = ?

A. 75 B. 89 C. 65 D. 82 E. None of these

Answer : Option A
2. If + means ÷, ÷ means –, – means x and x means +, then— 9 + 3 ÷ 5 – 3 x 7 = ?

A. 5 B. 15 C. 25 D. 10 E. None of these

Answer : Option E
3. If 'a' means '÷', 'b' means '+', 'c' means '–' and 'd' means 'x'. then— 11 b 15 c 8 a 4 d 5 = ?

A. 36 B. – 16 C. 26 D. 16 E. None of these

Answer : Option D

Simple Interest
1. How much time will it take for an amount of Rs. 450 to yield Rs. 81 as interest at 4.5% per annum of simple interest?

A. 3.5 years B. 4 years C. 4.5 years D. 5 years

Answer: Option B
Explanation: Time = ([latex]\frac {100 \times 81}{450 \times 4.5}[/latex]) years = 4 years.
2. An automobile financier claims to be lending money at simple interest, but he includes the interest every six months for calculating the principal. If he is charging interest of 10%, the effective rate of interest becomes:

A. 10% B. 10.25% C. 10.5% D. None of these

Answer: Option B
Explanation: Let the sum be Rs. 100. Then, S.I. for first 6 months = Rs. ([latex]\frac {100 \times 10 \times 1}{100 \times 2}[/latex]) = Rs. 5 S.I. for last 6 months = Rs. ([latex]\frac {105 \times 10 \times 1}{100 \times 2}[/latex]) = Rs. 5.25 So, amount at the end of 1 year = Rs. (100 + 5 + 5.25) = Rs. 110.25 Effective rate = (110.25 - 100) = 10.25%
Height and Distance
1. Two houses are in front of each other. Both have chimneys on their top. The line joining the chimneys makes an angle of 45° with the ground. How far are the houses from each other if one house is 25m and other is 10m in height?

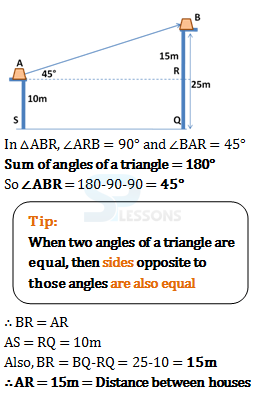
A. 18 m B. 12 m C. 7.5 m D. 15 m

Answer: Option D
Explanation:

2. Tree top’s angle of elevation is 30° from a point on the ground, 300m away from the tree. When the tree grew up its angle of elevation became 60° from the same point. How much did the tree grow?

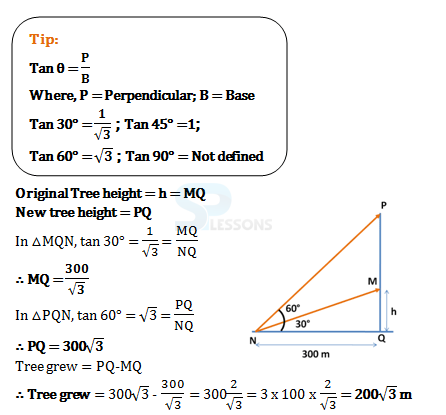
A. 100[latex]\frac {1}{2}[/latex] m B. 200[latex]\sqrt {3}[/latex] m C. 300(1/[latex]\sqrt {3}[/latex]) D. 200/[latex]\sqrt {3}[/latex] m

Answer: Option B
Explanation

3. A tree breaks and falls to the ground such that its upper part is still partially attached to its stem. At what height did it break, if the original height of the tree was 24 cm and it makes an angle of 30° with the ground?

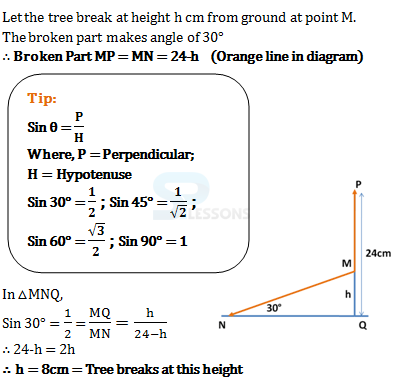
A. 12 cm B. 8 cm C. 9.5 cm D. 7.5 cm

Answer: Option B
Explanation:

Volume and Surface Area
1. 66 cubic centimeters of silver is drawn into a wire 1 mm in diameter. The length of the wire in meters will be:

A. 84 B. 90 C. 168 D. 336

Answer: Option A
Explanation: Let the length of the wire be h. Radius =[latex]\frac {1}{2}[/latex] mm = [latex]\frac {1}{20}[/latex] cm. Then, [latex]\frac {22}{7}[/latex] x [latex]\frac {1}{20}[/latex] x [latex]\frac {1}{20}[/latex] x h = 66. h = ([latex]\frac {66 \times 20 \times 20 \times 7}{22}[/latex]) = 8400 cm = 84 m.
2. A hollow iron pipe is 21 cm long and its external diameter is 8 cm. If the thickness of the pipe is 1 cm and iron weighs 8 g/cm3, then the weight of the pipe is:

A. 3.6 kg B. 3.696 kg C. 36 kg D. 36.9 kg

Answer: Option B
Explanation: External radius = 4 cm, Internal radius = 3 cm. Volume of iron = ([latex]\frac {22 \times [(4)^{2} - (3)^{2}] \times 21}{7}[/latex]) cm3 = ([latex]\frac {22}{7}[/latex] x 7 x 1 x 21) cm3 = 462 cm3. Weight of iron = (462 x 8) gm = 3696 gm = 3.696 kg.
3. A cistern 6m long and 4 m wide contains water up to a depth of 1 m 25 cm. The total area of the wet surface is:

A. 49 m[latex]^{2}[/latex] B. 50 m[latex]^{2}[/latex] C. 53.5 m[latex]^{2}[/latex] D. 55 m[latex]^{2}[/latex]

Answer: Option A
Explanation: Area of the wet surface = [2(lb + bh + lh) - lb] = 2(bh + lh) + lb = [2 (4 x 1.25 + 6 x 1.25) + 6 x 4] m[latex]^{2}[/latex] = 49 m[latex]^{2}[/latex].
Logarithm
1. Which of the following statements is not correct?

A. log[latex]_{10}[/latex] 10 = 1 B. log (2 + 3) = log (2 x 3) C. log[latex]_{10}[/latex] 1 = 0 D. log (1 + 2 + 3) = log 1 + log 2 + log 3

Answer: Option B
Explanation: (a) Since log[latex]_{a}[/latex] a = 1, so log[latex]_{10}[/latex] 10 = 1. (b) log (2 + 3) = log 5 and log (2 x 3) = log 6 = log 2 + log 3 log (2 + 3) ≠ log (2 x 3) (c) Since log[latex]_{a}[/latex]a 1 = 0, so log[latex]_{10}[/latex] 1 = 0. (d) log (1 + 2 + 3) = log 6 = log (1 x 2 x 3) = log 1 + log 2 + log 3. So, (b) is incorrect.
2. If log 27 = 1.431, then the value of log 9 is:

A. 0.934 B. 0.945 C. 0.954 D. 0.958

Answer: Option C
Explanation: log 27 = 1.431 log (3[latex]^{3}[/latex] ) = 1.431 3 log 3 = 1.431 log 3 = 0.477 log 9 = log(3[latex]^{2}[/latex]) = 2 log 3 = (2 x 0.477) = 0.954.
3. If log[latex]_{10}[/latex] 2 = 0.3010, then log[latex]_{2}[/latex] 10 is equal to:

A. [latex]\frac {699}{301}[/latex] B. [latex]\frac {1000}{301}[/latex] C. 0.3010 D. 0.6990

Answer: Option B
Explanation: log[latex]_{2}[/latex] 10 = [latex]\frac {1}{log_{10} 2}[/latex] = [latex]\frac {1}{0.3010}[/latex] = [latex]\frac {10000}{3010}[/latex] = [latex]\frac {1000}{301}[/latex].
Races and Games
1. In a 100 m race, A can give B 10 m and C 28 m. In the same race B can give C:

A. 18 m B. 20 m C. 27 m D. 9 m

Answer: Option B
Explanation: A : B = 100 : 90. A : C = 100 : 72. B : C =[latex]\frac {B}{A}[/latex] x [latex]\frac {A}{C}[/latex] = [latex]\frac {90}{100}[/latex] x [latex]\frac {100}{72}[/latex] = [latex]\frac {90}{72}[/latex]. When B runs 90 m, C runs 72 m. When B runs 100 m, C runs ([latex]\frac {72}{90}[/latex] x 100)m = 80 m. B can give C 20 m.
2. A and B take part in 100 m race. A runs at 5 kmph. A gives B a start of 8 m and still beats him by 8 seconds. The speed of B is:

A. 5.15 kmph B. 4.14 kmph C. 4.25 kmph D. 4.4 kmph

Answer: Option B
Explanation: A's speed = 5 x [latex]\frac {5}{18}[/latex] m/sec = [latex]\frac {25}{18}[/latex]m/sec. 18 Time taken by A to cover 100 m = (100 x [latex]\frac {18}{25}[/latex])sec = 72 sec. Time taken by B to cover 92 m = (72 + 8) = 80 sec. B's speed = ([latex]\frac {92}{80}[/latex] x [latex]\frac {18}{5}[/latex])kmph = 4.14 kmph.
3. In a 200 meters race A beats B by 35 m or 7 seconds. A's time over the course is:

A. 40 sec B. 47 sec C. 33 sec D. None of these

Answer: Option C
Explanation: B runs 35 m in 7 sec. B covers 200 m in ([latex]\frac {7}{35}[/latex] x 200) = 40 sec. B's time over the course = 40 sec. A's time over the course (40 - 7) sec = 33 sec.
Simplification
1. What should come in place of question mark (?) in the following question? 8100 ÷ 15 ÷ 5 =?

A. 215 B. 109.68 C. 185.56 D. 108 E. None of these

Answer: Option D
Solution: 8100 ÷ 15 ÷ 5 =? When this type of situation arises where the same type of signs are present then we solve the given expression from left to right. ⇒ (8100/15) ÷ 5 = ? ⇒ 540 ÷ 5 =? ⇒ ? = 108
2. Find the value of (25 × (10 + 5) – 15) ÷ 62

A. 20 B. 10 C. 60 D. 0 E. None of these

Answer: Option B
Explanation: Follow BODMAS rule to solve this question, as per the order is given below, Step-1- Parts of an equation enclosed in 'Brackets' must be solved first, and in the bracket, the BODMAS rule must be followed, Step-2- Any mathematical 'Of' or 'Exponent' must be solved next, Step-3-Next, the parts of the equation that contains 'Division' and 'Multiplication' are calculated, Step-4-Last but not least, the parts of the equation that contains 'Addition' and 'Subtraction' should be calculated. The given expression is, (25 × (10 + 5) – 15) ÷ 62 = (25 × 15 – 15) ÷ 62 = (375 - 15) ÷ 62 = 360 ÷ 62 = 360 ÷ 36 = 10
3. The price of 2 sarees and 4 shirts is Rs. 1600. With the same money, one can buy 1 saree and 6 shirts. If one wants to buy 12 shirts, how much shall he have to pay?

A. Rs. 1200 B. Rs. 2400 C. Rs. 4800 D. Cannot be determined E. None of these

Answer: Option B
Explanation: Let the price of a saree and a shirt be Rs. x and Rs. y respectively. Then, 2x + 4y = 1600 .... (i) and x + 6y = 1600 .... (ii) Divide equation (i) by 2, we get the below equation. => x + 2y = 800. --- (iii) Now subtract (iii) from (ii) x + 6y = 1600 (-) x + 2y = 800 ---------------- 4y = 800 ---------------- Therefore, y = 200. Now apply the value of y in (iii) => x + 2 x 200 = 800 => x + 400 = 800 Therefore x = 400 Solving (i) and (ii) we get x = 400, y = 200. Cost of 12 shirts = Rs. (12 x 200) = Rs. 2400.
Time and Distance
1. A car traveling with [latex]\frac {5}{7}[/latex] of its actual speed covers 42 km in 1 hr 40 min 48 sec. Find the actual speed of the car.

A. 17[latex]\frac {6}{7}[/latex] km/hr B. 25 km/hr C. 30 km/hr D. 35 km/hr

Answer: Option D
Explanation: Time taken = 1 hr 40 min 48 sec = 1 hr 40 [latex]\frac {4}{5}[/latex]min = 1 [latex]\frac {51}{75}[/latex]hrs =[latex]\frac {126}{75}[/latex]hrs. Let the actual speed be x km/hr. Then, [latex]\frac {5}{7}[/latex] x x [latex]\frac {126}{75}[/latex] = 42 x = [latex]\frac {42 \times 7 \times 75 }{5 \times 126}[/latex] = 35 km/hr.
2. Robert is traveling on his cycle and has calculated to reach point A at 2 P.M. if he travels at 10 kmph, he will reach there at 12 noon if he travels at 15 kmph. At what speed must he travel to reach A at 1 P.M.?

A. 8 kmph B. 11 kmph C. 12 kmph D. 14 kmph

Answer: Option C
Explanation: Let the distance traveled by x km. Then,[latex]\frac {x}{10}[/latex] - [latex]\frac {x}{15}[/latex] = 2 3x - 2x = 60 x = 60 km. Time taken to travel 60 km at 10 km/hr = [latex]\frac {60}{10}[/latex]hrs = 6 hrs. So, Robert started 6 hours before 2 P.M. i.e., at 8 A.M. Required speed =[latex]\frac {60}{5}[/latex] kmph. = 12 kmph.
3. A man covered a certain distance at some speed. Had he moved 3 kmph faster, he would have taken 40 minutes less. If he had moved 2 kmph slower, he would have taken 40 minutes more. The distance (in km) is:

A. 35 B. 36[latex]\frac {1}{3}[/latex] C. 37[latex]\frac {1}{2}[/latex] D. 40

Answer: Option D
Explanation: Let distance = x km and usual rate = y kmph. Then, [latex]\frac {x}{y}[/latex] - [latex]\frac {x}{y+3}[/latex] = [latex]\frac {40}{60}[/latex] => 2y(y + 3) = 9x ....(i) And,[latex]\frac {x}{y-2}[/latex] - [latex]\frac {x}{y}[/latex] = [latex]\frac {40}{60}[/latex] => y(y - 2) = 3x ....(ii) On dividing (i) by (ii), we get: x = 40.
Chain Rule
1. 5 mat-weavers can weave 5 mats in 5 days. At the same time, how many mats would be woven by 10 mat- weavers in 10 days?

A. 10 mats B. 15 mats C. 20 mats D. 30 mats

Answer: Option c
Explanation: Total 5 mats can be weaved in 5 days by 5 weavers. \[ 5 : x :: \begin{cases} 30 : 40 - - - (Men)\\ 5 : 3 - - - (Days) \end{cases} \] 5 × 5 × x = 10 × 10 × 5 x = [latex]\frac {10 \times 10 \times 5}{5 \times 5}[/latex] = 20 20 mats can be weaved in 10 days by 10 mat weavers.
2. If 30 men can do a piece of work in 20 hours, then in how many hours will 12 men do it?

A. 18 hours B. 30 hours C. 40 hours D. 50 hours

Answer: Option D
Explantion: As number of workers increase, the time required decreases. Hence, this is a problem related to indirect proportion. Workers (↑),Time (↓) Let the number of hours be x. 12 : 30 :: 20 : x [latex]\frac {20}{30}[/latex] = [latex]\frac {20}{X}[/latex] x = [latex]\frac {20 \times 30}{12}[/latex] = 50 12 men require 50 hours to complete the same work.
3. 18 men bind 900 books in 10 days. Find how many binders will be required to bind 600 books in 12 days?

A. 10 B. 11 C. 13 D. 15

Answer: Option A
Explanation: We have to find the number of binders. Let the number of binders be x. Direct Proportion:Less Books (↓),Less binders(↓) Indirect Proportion:More days (↑),Less binders (↓) \[ 18 : x :: \begin{cases} 900 : 600 - - - (Books) \\ 12 : 10 - - - (Days) \end{cases} \] x × 900 × 12 = 18 × 600 × 10 x = [latex]\frac {18 \times 600 \times 10}{900 \times 12}[/latex] = 10
Permutation and Combination
1. How many words can be formed by using letters of the word ‘DELHI’?

A. 50 B. 72 C. 85 D. 120

Answer: Option D
Explanation: The word ‘DELHI’ contains 5 letters Therefore, required number of words = [latex]^5P_{5}[/latex] = 5! = (5 × 4 × 3 × 2 × 1) = 120 120 words can be formed by using letters of the word ‘DELHI’
2. Find the number of ways the letters of the word ‘RUBBER can be arranged?

A. 450 B. 362 C. 250 D. 180

Answer: Option D
Explanation: The word ‘RUBBER’ contains 6 letters: 2R, 2B, 1 U, 1 E Therefore, The required Number of ways: [latex]\frac {N!}{(2R!) \times (2B!) \times (1U!) \times (1E!)}[/latex] = [latex]\frac {6!}{(2 × 1) \times (2 × 1) \times (1) \times (1)}[/latex] = [latex]\frac {6 \times 5 \times 4 \times 3 \times 2 \times 1}{4}[/latex] = 6 × 5 × 3 × 2 = 180
3. Find the value of [latex]^{20}c_{17}[/latex]

A. 1260 B. 1140 C. 2580 D. 3200

Answer: Option B
Explanation: [latex]^nc_{r}[/latex] =[latex]\frac {^np_{r!}}{r!}[/latex] [latex]^nc_{r}[/latex] = [latex]\frac {n!}{(r!) (n – r)!}[/latex] [latex]^{20}c_{17}[/latex] =[latex]\frac {20!}{(17!) (20 – 17)!}[/latex] [latex]^{20}c_{17}[/latex] =[latex]\frac {20 \times 19 \times 18 \times 17!}{(17!) (3)!}[/latex] [latex]^{20}c_{17}[/latex] =[latex]\frac {20 \times 19 \times 18}{3 \times 2 \times 1}[/latex] [latex]^{20}c_{17}[/latex] = 1140.
Surds and Indices
1. If a and b are whole numbers such that a[latex]^{b}[/latex] = 121, then find the value of (a – 1)[latex]^{b + 1}[/latex]

A. 0 B. 10 C. 10[latex]^{2}[/latex] D. 10[latex]^{3}[/latex]

Answer: Option D
Explanation: 121 = 11[latex]^{2}[/latex] , hence value of a = 11 and b = 2 can be considered. Therefore, the value of (a – 1)[latex]^{b + 1}[/latex] = (11 – 1)[latex]^{2 + 1}[/latex] = 10[latex]^{3}[/latex]
2. If 4 [latex]^{(x - y)}[/latex] = 64 and 4 [latex]^{(x + y)}[/latex] = 1024, then find the value of x.

A. 3 B. 1 C. 6 D. 4

Answer: Option D
Explanation: 4 [latex]^{(x - y)}[/latex] = 64 4 [latex]^{(x - y)}[/latex] = 64 = 43 Equation 1. x – y = 3 4 [latex]^{(x + y)}[/latex] = 1024 = 4[latex]^{5}[/latex] Equation 2. x + y = 5 Solving equation (1) and (2), we get x = 4 and y = 1 Crosscheck the answers by substituting the values of x and y in the given expression. 4 [latex]^{(4 – 1)}[/latex]= 4[latex]^{3}[/latex] = 64 and 4 [latex]^{(4 + 1)}[/latex] = 4[latex]^{5}[/latex] = 1024 Hence, the answers x = 4 and y = 1 are correct.
3. (1331)[latex]^{- (2/3)}[/latex]

A. –[latex]\frac {1}{11}[/latex] B. – [latex]\frac {11}{121}[/latex] C. [latex]\frac {1}{122}[/latex] D. [latex]\frac {121}{11}[/latex]

Answer: Option C
Explanation: Cube root of 1331 is 11. Therefore, (11)[latex]^{3 \times -(2/3)}[/latex] Remember the law of indices (xm)n = xmn (11)[latex]^{3 \times -(2/3)}[/latex] = 11[latex]^{-2}[/latex] x[latex]^{-1}[/latex] = [latex]\frac {1}{x}[/latex] Hence, 11[latex]^{-2}[/latex] = [latex]\frac {1}{112}[/latex] = [latex]\frac {1}{112}[/latex]
Pipes and Cistern
1. Two pipes A & B can fill the tank in 12 hours and 36 hours respectively. If both the pipes are opened simultaneously, how much time will be required to fill the tank?

A. 6 hours B. 9 hours C. 12 hours D. 15 hours

Answer: Option B
Explanation: If a pipe requires 'x' has to fill up the tank, then partly filled in 1 hr =[latex]\frac {1}{x}[/latex] If pipe A requires 12 hrs to fill the tank, then partly filled by pipe A in 1 hr =[latex]\frac {1}{12}[/latex] If pipe B requires 36 hrs to fill the tank, then part filled by pipe B 1 hr = [latex]\frac {1}{36}[/latex] Hence, part filled by (A + B) together in 1 hr =[latex]\frac {1}{12} + \frac {1}{36}[/latex] = [latex]\frac {48}{432}[/latex]= [latex]\frac {1}{9}[/latex] In 1 hr both pipes together fill [latex]\frac {1}{9}[/latex]th part of the tank. This means, together they fill the tank in 9 hrs.
2. An electric pump can fill a tank in 4 hours. Due to leakage in the tank, it took 4[latex]\frac {1}{2}[/latex] has to fill the tank. If the tank is full, how much time will the leak take to empty the full tank?

A. 8 hrs B. 16 hrs C. 21 hrs D. 36 hrs

Answer: Option D
Explanation: Consider a pipe fills the tank in 'x' hrs. If there is a leakage in the bottom, the tank is filled in 'y' hrs. The time is taken by the leak to empty the full tank = [latex]\frac {xy}{y – x}[/latex] hrs Time taken to empty the tank by the leak = 4 x (9/2) / (9/2 ) - 4 = (36/2 ) / ½ = 18/ ½ = 18 x 2 = 36 hrs
3. Two pipes can fill a tank in 8 hrs & 6 hrs respectively. If they are opened on alternate hours and if pipe A gets opened first, then in how many hours, the tank will be full?

A. 6 hrs B. 7 hrs C. 8 hrs D. 14 hrs

Answer: Option B
Explanation: Pipe A's work in 1 hr = 1/8 Pipe B's work in 1 hr = 1/6 Pipes (A+B)'s work in first 2 hrs when they are opened alternately = 1/8 + 1/6 = 7 /24 Now, In 4 hrs they fill : 2 X (7/24) = 7/12 In 6 hrs they fill : 3 X (7/24) = 7/8 After 6 hrs, part left empty = 1/8 Now it is A's turn to open up. In one hr it fills 1/8 of the tank. So, the tank will be full in = 6 hrs + 1 hr = 7 hrs.
Boats and Streams
1. If a boat travels with a speed of 10 km/hr in still water and the speed of the stream is 5 km/hr, what would be the time taken by boat to go 60 km downstream?

A. 2 hrs B. 4 hrs C. 6 hrs D. 8 hrs

Answer: OptionB
Explanation: In downstream, water stream increases the speed of the boat as they both are along the same directions. Hence, both the speeds are added. Thus, Downstream speed (Sd) = (x + y) km/hr --------------(1) Time = [latex]\frac {Distance}{Speed}[/latex] ------------------------------ (2) By substituting the values of 'x' & 'y' in equation (1), we get = 10 + 5 = 15 km/hr We have, Time = [latex]\frac {Distance}{Speed}[/latex] Time taken by a boat to travel 60 km downstream will be equal to the ratio of distance traveled to the downstream speed. Time taken by a boat =[latex]\frac {60}{15}[/latex] = 4 hours.
2. The speed of swimmer along with the flow of river is 40 km/hr and against the flow of river is 22 km/hr. What would be the speed of swimmer in still water?

A. 11 km/hr B. 31 km/hr C. 55 km/hr D. 62 km/hr

Answer: Option B
Explanation: In still water, we know that Speed of boat (x) = ([latex]\frac {1}{2}[/latex]) x [Downstream speed(Sd) + Upstream speed(Su)] With the given parameters like SD = 40 km/hr & SU = 22 km/hr, on substituting these values in above equation, we obtain x = [latex]\frac {1}{2}[/latex] [SD + SU] = [latex]\frac {1}{2}[/latex] [40 + 22] = 31 km/hr
Numbers
1. If 6 + 12 + 18 + 24 + --- = 1800, then find the number of terms in the series.

A. 21 B. 22 C. 23 D. 24

Answer: Option D
Explanation: This is an Arithmetic Progression, in which x = 6, y = 6, sum of terms = 1800 Sum of n terms =[latex]\frac {n}{2}[/latex][2x + (n – 1)y] Substituting the given values, we get 1800 = [latex]\frac {n}{2}[/latex] [2 × 6 + (n – 1)6] Solving we get, 1800 = 3n (n + 1) n(n +1) = 600 n[latex]^{2}[/latex] + n = 600 25 × 24 = 600 Therefore, n[latex]^{2}[/latex] + 25n – 24n – 600 = 0 (n + 25) (n – 24) = 0 24 and -25 are the two solutions obtained. Only positive value can be considered. Hence, n = 24 The number of terms in the series = 24
2. Find the largest 4 digit number which is divisible by 88.

A. 8844 B. 9999 C. 9944 D. 9930

Answer: Option C
Explanation: We know that the largest 4 digit number is 9999. Simply divide 9999 by 88. After dividing 9999 by 88 we get, 55 as remainder. The number is said to be completely divisible, only if the remainder is zero. Hence, we can find the required answer by subtracting the remainder obtained from the 4 digit number. Therefore, required number = 9999 – 55 = 9944
Partnership
1. Harry, John, and Smith start a shop by investing Rs. 27,000. Rs. 72,000 and Rs. 81,000 respectively. At the end of the year, the profit was distributed among them and Smith earns the share of Rs. 36,000. Find the total profit.

A. Rs. 1,10,000 B. Rs. 1,2,5000 C. Rs. 98,000 D. Rs. 80,000

Answer: Option D
Explanation: Ratio of shares of Harry, John and Smith = Ratio of their investments Harry : John : Smith = 27000 : 72000 : 81000 = 3 : 8 : 9 Given: Share of profit earned by Smith = Rs. 36,000 Total no. of shares = 3 + 8 + 9 = 20 shares Smith’s share =[latex] \frac {9}{20}[/latex] Let total profit = Rs. X [latex] \frac {36000}{X}[/latex] = [latex] \frac {9}{20}[/latex] X =[latex] \frac {36000 \times 20}{9}[/latex] = 80000 Total profit = Rs. 80,000
2. Two partners X and Y started a business by investing in the ratio of 5 : 8. Z joined them after 8 months investing an amount equal to that of Y. At the end of the year, 20 % profit was earned which is equal to Rs. 98,000. Find the amount invested by Z.

A. Rs. 213818.16 B. Rs. 223878.12 C. Rs. 203818.16 D. Rs. 219818.13

Answer: Option A
Explanation: Let the total profit be p. Given: 20 % profit is equal to Rs. 98,000 20 % of p = 98000 p = 490000 Capital of X = 5 x Capital of Y = 8 x Capital of Z = 8 x Therefore, (5x × 12) + (8x × 12) + (8x + 8) = 490000 × 12 220x = 5880000 x = Rs. 26727.27 We have find the amount invested by z. 8x = 8 x 26727.27 = Rs. 213818.16
Ratio and Proportion
1. If A : B : C = 3 : 4 : 7, then what is the ratio of (A / B) : (B / C) : (C / A)?

A. 63: 48: 196 B. 66: 49: 190 C. 56: 40: 186 D. 46: 38: 160

Answer: Option A
Explanation: If a = kb for some constant k, then we can say that a is directly proportional to b. A : B : C = 3 : 4 : 7 Assume, A = 3 k, B = 4 k, C = 7 k Therefore, [latex]\frac {A}{B}[/latex] = [latex]\frac {(3k)}{(4k)}[/latex] ,[latex]\frac {B}{C}[/latex] = [latex]\frac {(4k)}{(7k)}[/latex] , [latex]\frac {C}{A}[/latex] = [latex]\frac {(7k)}{(3k)}[/latex] [latex]\frac {A}{B}[/latex] = [latex]\frac {(3)}{(4)}[/latex],[latex]\frac {B}{C}[/latex] = [latex]\frac {(4)}{(7)}[/latex], [latex]\frac {C}{A}[/latex] = [latex]\frac {(7)}{(3)}[/latex] L.C.M of 3, 4, 7 is 84 (3 x 84) / 4 = 63 (4 x 84) / 7 = 48 (7 x 84) / 3 = 196 Ratio of (A/B) : (B/C) : (C/A) = 63:48:196
2. If Suresh distributes his pens in the ratio of 1/2: 1/4: 1/5: 1/7 between his four friends A, B, C, and D, then find the total number of pens Suresh should have?

A. 153 B. 150 C. 100 D. 125

Answer: Option A
Explanation: A : B : C : D = [latex]\frac {1}{2}[/latex] : [latex]\frac {1}{4}[/latex] : [latex]\frac {1}{5}[/latex] : [latex]\frac {1}{7}[/latex] 1. L.C.M of 2, 4, 5, 7 is 140 2. Find the number of pens each friend received --------- (To find no. of pens each friend has, multiply the ratio with the L.C.M. calculated) A = (1/2) x 140 = 70 B = (1/4) x 140 = 35 C = (1/5) x 140 = 28 D = (1/7) x 140 = 20 3. Total number of pens = (70 x + 35 x + 28 x + 20 x) = 153 x Minimum number of pens (x) = 1 Therefore, total number of pens = 153 pens.
Problems on H.C.F and L.C.M
1. Find the largest number of 4-digits divisible by 12, 15 and 18.

A. 9900 B. 9750 C. 9450 D. 9000

Answer: Option A
Explanation: The largest 4-digit number is 9999. Remember: The question may be asked in a tricky way. Here, largest number does not mean H.C.F.. We have to find a number which is divisible by 12, 15 and 18 Required largest number must be divisible by the L.C.M. of 12, 15 and 18 L.C.M. of 12, 15 and 18 12 = 2 × 2 × 3 15 =5 × 3 18 = 2 × 3 × 3 L.C.M. = 180 Now divide 9999 by 180, we get remainder as 99 The required largest number = (9999 – 99) =9900 Number 9900 is exactly divisible by 180.
2. Find L.C.M. of 1.05 and 2.1

A. 1.3 B. 1.25 C. 2.1 D. 4.30

Answer: Option C
Explanation: If numbers are in decimal form, convert them without decimal places. Therefore, the numbers are 105 and 210.
L.C.M. = 5 x 7 x 3 x 2 = 210 L.C.M. of 105 and 210 = 210 In decimal form: L.C.M. = 2.1
Banker’s Discount
1. Find the banker’s gain, if the present worth of a certain amount is Rs.2400 and the true discount is Rs.120.

A. 10 B. 12 C. 6 D. 20

Answer:Option C
Explanation: Banker's Gain = [latex]\frac {(T.D.)^{2}}{P.W.}[/latex] = [latex]\frac {(120)^{2}}{2400}[/latex] = Rs.6
2. The banker’s gain on a bill due 2 years hence at 10% per annum is Rs.10. What is the true discount?

A. 25 B. 50 C. 100 D. 75

Answer: Option B
Explanation: T.D. = ([latex]\frac {B.G \times 100}{R \times T}[/latex]) = ([latex]\frac {10 \times 100}{10 \times 2}[/latex]) =Rs. 50
Compound Interest
1. The value of a sewing machine depreciates at the rate of 10 % after every year. If at the end of 3 years, its value is Rs. 8748, then find its purchase price.

A. 8000 B. 10000 C. 12000 D. 15000

Answer: Option C
Explanation: If the cost of a machine is P1 and it decreases by R % annually, then the purchase price after n years is given by: P2 =P1 [latex](1 - \frac {R}{100})^{n}[/latex] We are given that the value of a sewing machine depreciates at the rate of 10 % after every year. After 3 years, its value is Rs. 8748. 8748 =P1 [latex](1 - \frac {10}{100})^{3}[/latex] P1 =Rs.12000 The purchase price of the sewing machine = Rs. 12000
2. Find the compound interest on Rs. 20,000 in 2 years at 4 % per annum, the interest being compounded half-yearly.

A. Rs. 1648.64 B. Rs. 1596.32 C. Rs. 14826.56 D. Rs. 11563.99

Answer: Option A
Explanation: Interest is compounded half-yearly, therefore, Amount = P [latex](1 + \frac {(R/2)}{100})^{2n}[/latex] - - - - - - - - - [Interest compounded Half-yearly] Given: Principal = Rs. 20000, Rate = 2 % per half-year, Time = 2 years = 4 half- years Amount = 20000 [latex](1 + \frac {(2)}{100})^{4}[/latex] Amount=Rs.21648.64 Compound Interest = Total amount – Principal = 21648.64 – 20000 = Rs. 1648.64
Area
1. When folded into two equal halves a rectangular sheet had a perimeter of 48cm for each part folded along one set of sides and the same is 66cm when folded along the other set of sides. Find the area of the sheet.

A. 1584 B. 1120 C. 792 D. 1320

Answer: Option B
Explanation: Let the sheet be folded along its breadth and its perimeter = 48cm Therefore, (l/2 + b) = 48 …... (i) Now, let the sheet be folded along its length, and the perimeter = 66cm (l + b/2)= 66 …... (ii) Solving (i) and (ii), we get, l = 56cm, b = 20cm Area = l X b Area = 1120 cm[latex]^{2}[/latex]
2. If the length is increased by 25%, by what percent the width of a rectangle should be decreased so as to keep the area the same.

A. 25% B. 20% C. 30% D. 10%

Answer: Option B
Explanation: Let the original length be l, and the width be b Therefore, the area = l X b Now, as the length is increased by 25%, the new length is (1.25 X l) and let the new width be x. As the area is same, 1.25 X l X x = l X b x = b/1.25 = 0.8b Therefore, the width is to be decreased by 20%.
Time and Work
1. Two painters 'P1' & 'P2' paint the bungalow in 3 days. If P1 alone can paint the bungalow in 12 days, in how many days can 'P2'' alone complete the same paint work?

A. 4 days B. 6 days C. 9 days D. 12 days

Answer: Option A
Explanation: If a person can do a part of work in 'n' days, the person's work in 1 day =[latex]\frac {1}{n}[/latex] As painters, P1 & P2 paint the bungalows in 3 days, then work done by both painters = [latex]\frac {1}{3}[/latex] As P1 paint it alone in 12 days, then work done by painter P1 = [latex]\frac {1}{12}[/latex] Work was done by painter P2 =[latex]\frac {1}{3}[/latex] – [latex]\frac {1}{12}[/latex] = [latex]\frac {4 - 1}{12}[/latex] = [latex]\frac {3}{12}[/latex] = [latex]\frac {1}{4}[/latex] Therefore, the same work will be completed by painter P2 in 4 days.
2. Pooja is twice as efficient as Aarti and takes 90 days less than Aarti to complete the job. Find the time in which they can finish the job together.

A. 30 days B. 45 days C. 60 days D. 90 days

Answer: Option C
Explanation: Since 'A' is 'm' times as efficient as 'B' & takes 'D' days less than 'B', then the time required to complete the job together is given by, T = m x [latex]\frac {D}{(m^{2}– 1)}[/latex] T = 2 x [latex]\frac {90}{(2^{2}– 1)}[/latex] = [latex]\frac {180 }{3}[/latex] = 60 days
Allegation or Mixture
1. In what ratio must wheat A at Rs. 10.50 per kg be mixed with wheat B at Rs. 12.30 per kg, so that the mixture be worth of Rs. 11 per kg?

A. 13: 5 B. 18 : 3 C. 17: 5 D. 11: 5

Answer: Option A
Explanation: Convert Rs into paise, to make the calculation easy
Ratio =[latex]\frac {(B – M)}{(M – A)}[/latex] The required ratio = 130 : 50 = 13 : 5
2. A shopkeeper has 100 kg of salt. He sells part of the total quantity A at 7% profit and the rest B at 17 % profit. If he gains 10 % profit on the whole quantity, then find how much is sold at 7 % profit?

A. 30 kg B. 35 kg C. 40 kg D. 45 kg

Answer: Option A
Explanation: Assume that A and B are two parts of the mixture. To determine the quantity A and B, first calculate the ratio of A: B. Given: 1) The selling price of the mixture with 10% profit = Rs. 110 2) With a 17 % profit, the selling price of A = Rs. 117 3) With 7 % profit, the selling price of B = Rs. 107 Now, this question can be easily solved by using the rule of the allegation
Now, the ratio of A: B = 3: 7 Let the quantity of part A be 3x and part B be 7x in the total quantity of 100 kg. Therefore, 3x + 7x = 100 10x = 100 x = 10 Quantity of part A = 3x = 3 x 10 = 30 kg Quantity of part B = 7x = 7 x 10 = 70 kg
Decimal Fraction
1. Convert 0.737373… into a vulgar fraction?

A. [latex]\frac {73}{99}[/latex] B. [latex]\frac {73}{100}[/latex] C. [latex]\frac {73}{90}[/latex] D. [latex]\frac {73}{900}[/latex]

Answer: Option A
Explanation: In a decimal fraction, if there are n numbers of repeated numbers after a decimal point, then just write one repeated number in the numerator and in denominator take n number of nines equal to repeated numbers you observe after the decimal point. 0.737373… is written as 0.[latex]\overline{73}[/latex] Numerator = 73 ---- (one repeated number) Denominator = 99 ---- (73 is the number which is repeated) Vulgar fraction = [latex]\frac {73}{99}[/latex]
2. If [latex]\frac {347.624}{0.0089}[/latex] = a, then find the value of [latex]\frac {347624}{0.0089}[/latex] = ?

A. [latex]\frac {a}{10}[/latex] B. 10 a C. [latex]\frac {a}{1000}[/latex] D. 1000a

Answer: Option C
Explanation: Given:[latex]\frac {347.624}{0.0089}[/latex] = a The value of [latex]\frac {347624}{0.0089}[/latex] ÷ 1000 = a ÷ 1000 = [latex]\frac {a}{1000}[/latex]
Probability
1. Tickets numbered 1 to 50 are mixed and one ticket is drawn at random. Find the probability that the ticket drawn has a number which is a multiple of 4 or 7?

A. 9/25 B. 9/50 C. 18/25 D. None of these

Answer: Option A
Explanation: S = {1, 2, 3, … , 49, 50} E = {4, 8, 12, 16, 20, 24, 28, 32, 36, 40, 44, 48, 7, 14, 21, 35, 42, 49} n(S) = 50 n(E) = 18 P(E) = n(E)/n(S) = 18/50 = 9/25
2. From a pack of 52 cards, one card is drawn at random. Find the probability that the drawn card is a club or a jack?

A. 17/52 B. 8/13 C. 4/13 D. 1/13

Answer: Option C
Explanation: n(S) = 52 n(E) = 16 P(E) = n(E) / n(S) = 16/ 52 = 4/13
Average
1. Find the average of all numbers between 5 and 49 which are divisible by 5.

A. 20 B. 25 C. 30 D. 35

Answer: Option B
Explanation: The numbers divisible by 5 are: 5, 10, 15, 20, 25, 30, 35, 40, 45. Average = [latex]\frac {Sum of Quantities}{Number of Quantities}[/latex] = [latex]\frac {(5 + 10 + 15 + 20 + 25 + 30 + 35 + 40 + 45)}{9}[/latex] = [latex]\frac {225}{9}[/latex] = 25
2. The average of 15 numbers is 15. If the average of first five numbers is 14 and that of other 9 numbers is 16, then find the middle number.

A. 12 B. 11 C. 10 D. 9

Answer: Option B
Explanation: Given: Average of 15 numbers = 15, Average of 5 numbers = 14, Average of 9 numbers = 16 Average = [latex]\frac {Total Numbers}{No. of Numbers}[/latex] 15 = [latex]\frac {Total Numbers}{15}[/latex] Therefore, total numbers = 15 x 15 = 225 Middle number = (Total numbers) – [(Average of 5 num x no of num) + ( Average of 9 num x no of num)] = (225) – [(14 x 5) + (16 x 9)] = (225) – [214] = 11 Therefore, the middle number is 11
3. In a school, average marks of three batches of 40, 50 and 60 students respectively is 45, 55 and 70. Find the average marks of all the students.

A. 54.78 B. 55.23 C. 50.36 D. 58.33

Answer: Option D
Explanation: We know, Average = [latex]\frac {Sum of Quantities}{Number of Quantities}[/latex] Here, Number of quantities = Number of students in each batch As average marks of students are given, calculate total marks of each batch first. So total marks for Batch 1 = (40 x 45) = 1800 Batch 2 = (50 x 55) = 2750 Batch 3 = (60 x 70) = 4200 Sum of marks = (1800 + 2750 + 4200) = 8750 Therefore, Required Average =[latex]\frac {(Sum of Works)}{(Total No. of Students in each batch)}[/latex] = [latex]\frac {(8750)}{(40 + 50 + 60)}[/latex] = 58.33
Stocks and Share
1. Find the number of shares that can be bought for Rs.8200 if the market value is Rs.20 each with brokerage being 2.5%.

A. 450 B. 500 C. 400 D. 410

Answer: Option C
Explanation: Cost of each share = (20 + 2.5% of 20) = Rs.20.5 Therefore, number of shares = 8200/20.5 = 400
2. Find the market value of the stock if 6% yields 10%.

A. 60 B. 70 C. 80 D. 100

Answer: Option A
Explanation: Let the investment be Rs.100 for an income of Rs.10 Therefore, for an income of Rs.6, the investment = 600/10 = Rs.60
Square Root and Cube Root
1. Find the square root of 5929

A. 49 B. 33 C. 77 D. 73

Answer: Option C
Explanation: Remember the trick discussed in Quick Tips and Tricks Step 1: Split the number 59 29 7[latex]^{2}[/latex] = 49 is the nearest number to 59.Hence, the digit in ten’s place is 7. Step 2: Last digit of number 29 is 9. Therefore, 3 or 7 are the digits in unit’s place. Multiply 3 by next consecutive higher number i.e. 4 3 × 4 = 12 But 12 < 59, hence consider the largest number among 3 and 7. The digit in unit’s place is 7. Hence, the square root of 5929 is 77
2. 28[latex]\sqrt {x}[/latex] + 1426 = [latex]\frac {3}{4}[/latex]of 2984. Find x

A. 659 B. 694 C. 841 D. 859

Answer: Option C
Explanation: 28[latex]\sqrt {x}[/latex] + 1426 = [latex]\frac {3}{4}[/latex]of 2984. 28[latex]\sqrt {x}[/latex] + 1426 = [latex]\frac {3}{4}[/latex]× 2984= 2238 28[latex]\sqrt {x}[/latex] = 2250 – 1426 = 812 [latex]\sqrt {x}[/latex] = 29 x = 841
Problems on Ages
1. What is John’s present age, if after 10 years his age will be 5 times his age 5 years back.

A. 6.2 years B. 7.7 years C. 8.7 years D. 10 years

Answer: Option C
Explanation: 1) Let John’s present age be x 2) John’s age before 5 years = (x - 5) 3) John’s age after 10 years = (x + 10) We are given that, John’s age after 10 years (x + 10) is 5 times his age 5 years back (x – 5) Therefore, (x + 10) = 5 (x – 5) Solving the equation, we get x + 10 = 5x – 25 4x = 35 x = 8.75 years
2. One year ago, the ratio of Harry and Peter age’s was 5: 6 respectively. After 4 years, this ratio becomes 6: 7. How old is Peter?

A. 25 years B. 26 years C. 31 years D. 35 years

Answer: Option C
Explanation: If ages in the numerical are mentioned in ratio A: B, then A: B will be Ax and Bx. We are given that age ratio of Harry : Pitter = 5 : 6 1) Harry’s age = 5x and Peter’s age = 6x 2) One year ago, their age was 5x and 6x. Hence at present, Harry’s age = 5x +1 and Peter’s age = 6x +1 3) After 4 years, Harry’s age = (5x +1) + 4 = (5x + 5) Peter’s age = (6x +1) + 4 = (6x + 5) 4) After 4 years, this ratio becomes 6 : 7. Therefore, [latex]\frac {Harry’s Age}{6}[/latex] = [latex]\frac {Peter’s Age}{7}[/latex] (5x + 5) / (6x + 5) = 6 / 7 7 (5x + 5) = 6 (6x + 5) X = 5 Peter’s present age = (6x + 1) = (6 x 5 + 1) = 31 years Harry’s present age = (5x + 1) = (5 x 5 + 1) = 26 years