1. “Matrimandir” is located in:

A. Pondicherry B. Chennai C. Panaji D. Hyderabad

Answer: Option A
2. Which among the following sub-school of Vedanta is followed by ISCON?

A. Shuddhādvaita B. Achintya Bhedābheda C. Purnādvaita or Integral Advaita D. Modern Vedānta

Answer: Option B
3. Chenab River also known as Chandrabhaga forms with the merging of Chandra and Bhaga Rivers near which among the following places?

A. Leh B. Lahaul & Spiti C. Sri Nagar D. Mithankot (Pakistan)

Answer: Option B
4. Famous tourist spots viz. Chatham Saw Mill, Wandoor Beach, Mount Harriet & Limestone Caves are located in which state?

A. Goa B. Andaman & Nicobar Islands C. Lakshadweep D. Tamil Nadu

Answer: Option B
5. The efforts of which among the following leaders were successful passing of the Bombay Primary Education Act?

A. Ganesh Vasudev Mavalanka B. R. K. Shanmukham Chetty C. Vitthal Bhai Patel D. Govind Ballabh Pant

Answer: Option C
6. Which among the following indicates Vitamin B12?

A. Niacin B. Pyridoxine C. Cobalamine D. Thiamine

Answer: Option C
7. “Pratham” the first animal born in 1990 by the IVF (In vitro Fertilization) at the National Dairy Research Institute, Karnal was a ________ ?

A. Cow B. Buffalo C. Sheep D. Goat

Answer: Option B
8. Genetic Modification (GM) technique RIDL was in news. RIDL is being developed for combating which of the following disease?

A. Swine Flu B. Malaria C. Cancer D. AIDS

Answer: Option B
9. Who among the following established that genetic code of all organisms is spelled out in three-letter words, each set of three nucleotides codes for a

A. Hargobind Khorana B. Barbara McClintock C. Theodor O. Diener D. Joseph L. Goldstein

Answer: Option A
Direction: Read each sentence to find out whether there is any grammatical error in it. The error, if any will be in one part of the sentence. The letter of that part is the answer. If there is no error, the answer is 'E'. (Ignore the errors of punctuation, if any).
10.

A. Several issues raising B. in the meeting could C. be amicably resolved D. due to his tactful handling.

Answer: Option A
Direction: Each question consists of two words that have a certain relationship to each other followed by four pairs of related words, Select the pair which has the same relationship.
11. HOPE:ASPIRES

A. love:elevates B. film:flam C. fib:lie D. fake:ordinary

Answer: Option C
Direction: Some proverbs/idioms are given below together with their meanings. Choose the correct meaning of proverb/idiom, If there is no correct meaning given, E (i.e.) 'None of these' will be the answer.
12. To make clean breast of

A. To gain prominence B. To praise oneself C. To confess without of reserve D. To destroy before it blooms

Answer: Option C
Direction: Which of the phrases given below each sentence should replace the phrase printed in bold type to make the grammatically correct? If the sentence is correct as it is, mark 'E' as the answer.
13. We were still standing in the queue when the film was beginning.

A. film began B. film had begun C. beginning of the film was over D. film begins

Answer: Option B
Direction(14-15): In questions given below out of four alternatives, choose the one which can be substituted for the given word/sentence.
14. One who dabbles in fine arts for the love of it and not for monetary gains

A. Connoisseur B. Amateur C. Professional D. Dilettante

Answer: Option B
15. A school boy who cuts classes frequently is a

A. Defeatist B. Sycophant C. Truant D. Martinet

Answer: Option C

1. The angles of a triangle are (x + 5)°, (2x – 3)° and (3x + 4)°. The value of x is

A. 30 B. 31 C. 29 D. 28

Answer: Option C
Explanation: Sum of angles of a triangle = 180° ∴ x + 5 + 2x – 3 + 3x + 4 = 180° ⇒ 6x + 6 = 180° ⇒ 6x = 174° ⇒ x = 29
2. If cosΘ + secΘ = 2 ,then the value of [latex]{cos}^{68}[/latex]Θ + [latex]{sec}^{68}[/latex]Θ equal to

A. 1 B. 2 C. 3 D. 68

Answer: Option B
Explanation: cosΘ + secΘ = 2 or, cosΘ + [latex]\frac{1}{cosΘ}[/latex] = 2 ∴ cosΘ = 1 ∴ secΘ = [latex]\frac{1}{cosΘ}[/latex] Now, [latex]{cos}^{68}[/latex]Θ + [latex]{sec}^{68}[/latex]Θ = 1 + 1 = 2
3. The value of sin (45° + θ) – cos (45° – θ) is

A. 1 B. 0 C. 2 cos θ D. 2 sin θ

Answer: Option B
Explanation: sin(45° + θ) – cos(45° – θ) = sin{90° – (45° – θ)} – cos (45° – θ) = cos (45° – θ) – cos (45° – θ) {∵sin(90 – A) = cos A } = 0
4. What is cosec (75° + Θ) – sec (15° – Θ) – tan (55° + Θ) + cot (35° – Θ) equal to?

A. -1 B. 0 C. 1 D. [latex]\frac{3}{2}[/latex]

Answer: Option B
Explanation: cosec (75° + Θ) – sec (15° – Θ) – tan (55° + Θ) + cot (35° – Θ) = cosec (75° + Θ) – sec [90° – (75° – Θ)] – tan (55° + Θ) + tan [90 – (55° – Θ)] = cosec (75° + Θ) – cosec (75° + Θ) – tan (55° + Θ) + tan (55° + Θ) = 0.
5. If tanΘ + cotΘ = 16, then find the ratio of [latex]{tan}^{2}[/latex]Θ +[latex]{cot}^{2}[/latex]Θ to [latex]{tan}^{2}[/latex]Θ + [latex]{cot}^{2}[/latex]Θ + 20 tanΘ.cotΘ

A. 64 : 65 B. 129 : 137 C. 27 : 29 D. 127 : 137

Answer: Option D
Explanation: Given, tanΘ + cotΘ = 16 Squaring both sides, we get [latex]{tan}^{2}[/latex]Θ + 2tanΘ . cotΘ + [latex]{cot}^{2}[/latex]Θ = 256 or, [latex]{tan}^{2}[/latex]Θ+ [latex]{cot}^{2}[/latex]Θ = 256 – 2 ∴ [latex]{tan}^{2}[/latex]Θ + [latex]{cot}^{2}[/latex]Θ = 254 Now, [latex]{tan}^{2}[/latex]Θ + [latex]{cot}^{2}[/latex]Θ + 20tanΘ.cotΘ [latex]{tan}^{2}[/latex]Θ + [latex]{cot}^{2}[/latex]Θ + 20tanΘ . [latex]\frac{1}{tan}[/latex]Θ = 254 + 20 = 274 Reqd. ratio = [latex]\frac{ 254 }{ 274 }[/latex] = [latex]\frac{ 127 }{ 137 }[/latex] = 127 : 137
6. PQ is a chord of a circle with centre O and SOR is a line segment originating from a point S on the circle and intersecting PQ produced at R such that QR = OS. If ∠QRO = 30° then ∠POS = ?

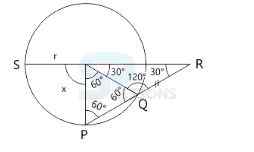
A. 40° B. 70° C. 90° D. 60°

Answer: Option C
Explanation: Let radius be 'r' and ∠POS = x° ΔOQR isosceles ∴∠QOR = 30° ∴ ∠OQR = 120° (Sum of all angles of ΔOQR = 180°) ∴ ∠OQP = 60° (Supplementary agnle) ΔOPQ isoceles since OP = OQ = r ∴ ∠OQP = 60° = ∠OQP ∴ ∠ POQ = 60° = [Sum of all angle of Δ = 180° ] Now SOR is a straight line ∴ x + 60° + 30° = 180° ∴ x = 90°
7. O and O' are repectively the orthocentre and cicumcentre of an acute angled triangle PQR. the point P and O are joined and produced to meet the side QR at S. If ∠PQS = 60° and ∠QO'R = 130° then ∠RPS = ?

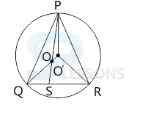
A. 45° B. 35° C. 60° D. 75°

Answer: Option B
Explanation: ∠ PQS = 60° ∠QO'R = 130° ∠ QPR = [latex]\frac{1}{2}[/latex] × 130° = 65° ⇒ ∠ QRP = 180° – 60° – 65° = 55° ⇒ ∠PO'Q = 110° In Δ QO'R QO' = O'R ⇒ ∠O'QR = ∠O'RQ = 25° ∵ ∠O'QR + ∠O'RQ = 50° ⇒ ∠PQO' + ∠QPO' = 35° ∵ ∠PQO' + ∠QPO' = 70° Similarly, ∠O'PR = 30° ∴ ∠RPS = 35°
8. In the given figure below, ∠AOB = 48° and AC and OB intersect each other at right angles. What is the measure of ∠OBC? (O is the centre of the circle)

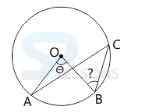
A. 44° B. 66° C. 67° D. 78.5°

Answer: Option B
Explanation: ∠AOB = 48° So, ∠ACB = [latex]\frac{1}{2}[/latex] ∠AOB = [latex]\frac{1}{2}[/latex] × 48° = 24° (As angles made by same arc AB) Given AC and OB intersect each other at a right angle. ∠ CQB = 90° ∠ CBQ = 180° – (90° + 24°) = 66° so , ∠ OBC = 66°
9. In a right angled triangle, the circumcentre of the triangle lies.

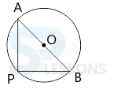
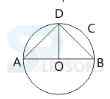
A. inside the triangle B. outside the triangle C. on the midpoint of hypotenous D. on one vertex

Answer: Option C
Explanation: ∠APB = 90° AB = Diameter = Hypotenous of triangle APB As the angle of the semicircle is a right angle so, the circumcentre lies on the midpoint of the hypotenuse
10. AB is the diameter of a circle with center O and radius OD is perpendicular to AB. Find the angle BAD

A. 60° B. 45° C. 30° D. 75°

Answer: Option B
Explanation: In ∆ AOD : OA = OD (radius) ∠ AOD = 90 ( as OD is perpendicular to AB ) So ∆ AOD is isosceles having OA and OD sides equal and one angle as 90 So the remaining two angle are 45 each Hence ∠ BAD = 45°
11. Three dice are thrown together. Find the probability of getting a total of at least 6 ?

A. [latex]\frac{103}{216}[/latex] B. [latex]\frac{103}{208}[/latex] C. [latex]\frac{103}{108}[/latex] D. [latex]\frac{36}{103}[/latex]

Answer: Option C
Explanation: Since one die can be thrown in six ways to obtain any one of the six numbers marked on its six faces ⇒ Total number of elementary events = 6 x 6 x 6 = 216 Let A be the event of getting a total of at least 6. Then Ā denotes the event of getting a total of less than 6 i.e. 3, 4, 5. ⇒ Ā = { (1,1,1), (1,1,2), (1,2,1), (2,1,1), (1,1,3),(1,3,1), (3,1,1), (1,2,2), (2,1,2), (2,2,1) } So, a favorable number of cases = 10 P(Ā) = [latex]\frac{10}{216}[/latex] 1 – P (A) = [latex]\frac{10}{216}[/latex] P (A) = 1 - [latex]\frac{10}{216}[/latex] [latex]\frac{103}{108}[/latex]
Direction: From a box containing 8 yellow and 5 white pens, three are drawn one after the other.
12. Find the probability of all three pens being yellow if the pens drawn are not replaced?

A. [latex]\frac{336}{176}[/latex] B. [latex]\frac{128}{429}[/latex] C. [latex]\frac{113}{176}[/latex] D. [latex]\frac{336}{2197}[/latex]

Answer: Option A
Explanation: If the pens are being drawn one after another, the probability of drawing any color of pens for every fresh draw changes. [latex]\frac{8}{13}[/latex] X [latex]\frac{7}{12}[/latex] X [latex]\frac{6}{11}[/latex] = [latex]\frac{336}{1716}[/latex]
Direction: From a box containing 8 yellow and 5 white pens, three are drawn one after the other.
13. Find the probability of all three pens being yellow if the pen drawn is replaced by another yellow-colored pen before the next pen is picked.

A. [latex]\frac{336}{2197}[/latex] B. [latex]\frac{512}{2197}[/latex] C. [latex]\frac{40}{2197}[/latex] D. [latex]\frac{57}{91}[/latex]

Answer: Option B
Explanation: When the pens drawn are replaced, we can see that the number of pens available for drawing out will be the same for every draw. This means that the probability of a yellow pen appearing in every draw are will be the same. [latex]\frac{8}{13}[/latex] X [latex]\frac{8}{13}[/latex] X [latex]\frac{8}{13}[/latex] = [latex]\frac{512}{2197}[/latex]
Direction: Kindly study the following information carefully and answer the question that follows: A box contains 4 white, 6 green, 2 red and 5 yellow pens.
14. If two pens are picked at random, what is the probability that both of them are green?

A. [latex]\frac{5}{136}[/latex] B. [latex]\frac{1}{136}[/latex] C. [latex]\frac{15}{136}[/latex] D. [latex]\frac{8}{15}[/latex]

Answer: Option C
Explanation: n(S) = [latex]{17}_{{C}_{2}}[/latex] = [latex]\frac{17 × 16}{2}[/latex]= 136 n(E) = [latex]{6}_{{C}_{2}}[/latex] = [latex]\frac{5 × 16}{1 × 2 }[/latex]= 15 Reqd probability = [latex]\frac{15}{136 }[/latex]
15. A box contains 21 balls numbered 1 to 21. A ball is drawn and then another ball is drawn without replacement. What is the probability that both balls are even-numbered?

A. [latex]\frac{2}{7}[/latex] B. [latex]\frac{8}{21}[/latex] C. [latex]\frac{3}{14}[/latex] D. [latex]\frac{5}{21}[/latex]

Answer: Option C
Explanation: There are 10 even numbers in the group 1-21. The probability that the first ball is even-numbered = [latex]\frac{10}{21}[/latex] Since the ball is not replaced there are now 20 balls left, of which 9 are even-numbered. [latex]\frac{9}{20}[/latex] Required probability = [latex]\frac{10}{21 }[/latex] x [latex]\frac{9}{20 }[/latex] = [latex]\frac{9}{42 }[/latex] = [latex]\frac{3}{14 }[/latex]