1. The concept of Eight-fold path forms which of the following themes?

A. Dipavamsa B. Divyavadana C. Mahaparinibban Sutta D. Dharma Chakara Pravartana Sutta

Answer: Option D
2. In the Mahayana Buddhism, the Bodhisattva Avalokitesvara was also known by which of the following names?

A. Vajrapani B. Manjusri C. Padmapani D. Maitreya

Answer: Option C
3. Which one of the following scripts of ancient India was written from right to left?

A. Brahmi B. Nandnagari C. Sharada D. Kharoshti

Answer: Option D
4. Which one of the following was a Saiva sect in ancient India?

A. Ajivika B. Mattamayura C. Mayamata D. Isanasivagurudevapaddhati

Answer: Option A
5. Which one of the following sculptures invariably used green schist as the medium?

A. Maurya sculptures B. Mathura sculptures C. Bharhut sculptures D. Gandhara sculptures

Answer: Option C
6. The “Ninety East Ridge” is a submarine volcanic ridge located in __?

A. Pacific Ocean B. Atlantic Ocean C. Atlantic Ocean D. Arctic Ocean

Answer: Option C
7. The “Helmand Province” of Afghanistan is famous for cultivation of __:

A. Tobacco B. Opium C. wheat D. Cotton

Answer: Option B
8. The cities of ‘Hiroshima’ and ‘Nagasaki’ are located on which among the following Islands of Japanese Archipelago?

A. Honshu and Kyushu respectively B. Honshu and Shikoku respectively C. Hokkaido and Kyushu respectively D. Kyushu and Shikoku respectively

Answer: Option A
9. Which of the following countries are separated by the Strait of Gibraltar?

A. Portugal and Morocco B. Algeria and Spain C. Morroco and Spain D. Algeria and Portugal

Answer: Option C
10. Which of the following places of the world is known for ‘Guano’, a uniquely-produced natural fertilizer which has a high concentration of nitrates?

A. Tierra del Feugo B. Atacama desert C. Minas Gerais of Brazil D. Coastal headlands and Islands of Peru

Answer: Option D
11. Lysergic acid diethylamide (LSD) is a drug used as a :

A. Steroid B. Sedative C. Analgesic D. Hallucinogen

Answer: Option D
12. Amalgam’ is a term used for an alloy of a metal with :

A. Copper B. Mercury C. Lead D. Aluminium

Answer: Option D
13. Gammaxene, D.D.T. and Bleaching powder are important compounds of :

A. Copper B. Mercury C. Lead D. Aluminium

Answer: Option B
14. L.P.G. is a hydrocarbon consisting of a mixture of :

A. Methane and Butane B. Propane and Butane C. Ethane and Propane D. Ethane and Butane

Answer: Option B
15. What is Kerogen oil?

A. Its an unconventional oil produced from the pyrolysis, hydrogenation, or thermal dissolution of Oil Shales B. Its a light crude oil contained in petroleum-bearing formations of shales C. Its an unconventional oil produced from the pyrolysis, hydrogenation, or thermal dissolution of environmental wastes D. It’s a new form of vegetable oil prepared artificially in laboratory

Answer: Option A
16. The jurisdiction covering the Andaman and Nicobar islands falls under the supervision of __:

A. A circuit bench of the Bombay High Court at Port Blair B. A circuit bench of the Madras High Court at Port Blair C. A circuit bench of the Calcutta High Court at Port Blair D. A circuit bench of Supreme Court of India at Port Blair

Answer: Option C
17. How long a person should have practiced in a High Court to be eligible to be appointed as a Judge of Supreme Court of India?

A. 10 Years B. 12 Years C. 15 Years D. 20 Years

Answer: Option A
18. As per Indian Mythology, Dhumravarna is an incarnation or avatara of _______?

A. Vishnu B. Shiva C. Ganesha D. Hanuman

Answer: Option C
19. Which of the following cultural organizations was established by Maulana Abul Kalam Azad, the first Education Minister of independent India.?

A. Indian Council for Cultural Relations B. Centre for Cultural Resources and Training C. Lalit Kala Akademi D. Sahitya Academy

Answer: Option A
20. In which of the following states of India, Yakshagana, a dance drama is popular

A. Tamil Nadu B. Karnataka C. Kerala D. Madhya Pradesh

Answer: Option B
21. What does the M in M-banking stands for?

A. prohibition of a banking company form creating a charge upon anu unpaid capital of the company. B. system of licensing of banks by RBI C. regarding holidays of the bank D. none of the above

Answer: Option A
22. As per which act, holidays are provided in the banks?

A. RBI act B. Banking regulation act C. As per orders of govt. D. Banking nationalization act.

Answer: Option B
23. World investment report is published by?

A. UNDP B. World bank C. IMF D. UNCTAD

Answer: Option D
24. Which of the following schemes are not meant for investment purposes?

A. national saving certificate B. mutual funds C. infrastructure bonds D. letter of credit

Answer: Option D
25. What was the purpose of setting up Narsimhan committee-2?

A. efficiency and productivity of financial institution B. banking reform process C. export of it sector D. fiscal reform process

Answer: Option B
26. Merchant banking in India is governed by

A. SEBI B. RBI C. IRDA D. ministry of finance

Answer: Option A
27. Money laundering means

A. hiding of income source mainly to avoid income tax B. money acquired through criminal sources. C. money acquired from undisclosed foreign sources. D. process of conversion of money obtained illegally to appear to have originated from legitimate sources

Answer: Option D
28. If you wish to purchase US dollars to travel abroad, you will approach

A. ministry of finance B. US embassy C. any bank branch authorized for such activity D. RBI

Answer: Option C
29. "Disguised unemployment" Denotes:

A. a situation where workers are disguised B. a situation where too many workers are doing a limited amount of work. C. a situation where workers are doing a limited amount of work D. None of the above

Answer: Option B
30. Foreign Trade Policy is Framed by :

A. RBI B. EXIM Bank C. DGFT D. Ministry of Commerce, Government of India.

Answer: Option D 31. The "bank rate " is :

A. Free to fluctuate according to the forces of demand and supply B. Set by the Reserve Bank of India C. set by the Reserve Bank of India as directed as directed by the Union Ministry of Finance D. Set by the Reserve Bank of India as directed as directed by the Indian Banks' Association

Answer: Option B
32. The term "exchange arbitrage " is the :

A. Arbitration of exchange disputes B. Simultaneous buying selling of foreign exchange to make a profit because interest rates vary in different countries C. Simultaneous purchase of a currency in one market and its sale in another market wit a view to realise profit D. buying of foreign currency to realise a future profit when it appreciates

Answer: Option C
33. The law regarding negotiable instruments is contained in :

A. The Bill of Exchange Act, 1881 B. The Banking Regulation Act, 1949 C. The Cheques Act, 1881 D. The Negotiable Instruments Act, 1881

Answer: Option D
34. " Black Revolution " is associated with :

A. Tea plantation B. Coffee Plantation C. Rubber Plantation D. Printing Ink

Answer: Option C
35. "channel Financing" means:

A. Financing of supply-delivery chain, i.e.., dealer of identified large corporate entities financed by banks B. Laying of agriculture canals C. Financing through NBFCs D. None of the above

Answer: Option A
36. Which is the Literary award?

A. Dronacharya Awards B. R. D. Birla Award C. Jawaharlal Nehru Award D. Jnanpith award

Answer: Option D
37. Dronacharya Award is given to which field?

A. Literature B. Sports C. Education D. Music

Answer: Option B
38. The Nobel Prizes are not presented for

A. Physics B. Chemistry C. Literature D. Arts

Answer: Option D
39. Which is India's highest civilian award?

A. National Award B. Padma Bhushan C. Padma Vibushan D. Bharat Ratna

Answer: Option D
40. In which year was the Bharat Ratna instituted?

A. 1954 B. 1952 C. 1956 D. 1945

Answer: Option A
41. Which is India's highest Civilian honour?

A. Ashoka Chakra B. Padma bhushan C. Padma Sri D. Padma Vibushan

Answer: Option D
42. Who was the first recipient of Bharat Ratna?

A. Dr. Radhakrishnan B. Jawaharlal Nehru C. Mahatma Gandhiji D. Indira Gandhi

Answer: Option A
43. Who was the first recipient of Padma Vibhushan?

A. Nand Lal Bose B. Satyendra Nath Bose C. Dr. Bir Bhan Bhatia D. Jawaharlal Nehru

Answer: Option B
44. Which is India?s highest military honour?

A. Param Vir Chakra B. Vir Chakra C. Maha Vir Chakra D. Bharat Ratna

Answer: Option A
45. The Reserve Bank of India will transfer its surplus profit of 65,896 crore rupees to the Centre. This amount is ___ percent higher than previous year.

A. 5% B. 19% C. 25% D. 33%

Answer: Option C
46. RBI has relaxed norms for which of the following bonds?

A. Masala bonds B. Rupee denominated overseas bonds C. Green bonds D. Both A and B

Answer: Option D
47. RBI has expanded the definition of which scheme?

A. Banking ombudsman scheme B. Banking internal stakeholders scheme C. Personalised banking scheme D. None of the above

Answer: Option A
48. RBI kept repo rates ____ in second bi-monthly monetary policy review.

A. Higher B. Lower C. Unchanged D. None of the above

Answer: Option C
49. RBI has tightened the rules around JLFs. What does JLF stand for?

A. Joint Lenders Forum B. Joint Liability Forum C. Joint Liaison Forum D. None of the above

Answer: Option A
50. According to RBI, India’s forex reserves rose to which record high?

A. USD 372.73 billion B. USD 373.73 billion C. USD 374.73 billion D. USD 375.73 billion

Answer: Option A

Prepositions 1. It is very dangerous to intrude ___________ the enemy's camp

A. in B. into C. on D. through

Answer: Option C
1. Very often we do not get what we find -------

A. for B. about C. at D. on

Answer: Option A
3. The reward was not commensurate ---------- the work was done by us.

A. on B. for C. with D. order

Answer: Option C
Active Voice and Passive Voice
4. We ———————- for the examination.

A. Have preparing B. Are preparing C. Had preparing D. Have been prepared

Answer: Option B
5. The Romans expected to conquer Carthage.

A. The Romans expected, to have conquered Carthage. B. Carthage was expected to be conquered by the Romans. C. The Romans were expected to conquer Carthage. D. It was expected by the Romans that they would conquer Carthage.

Answer: Option D
6. He teaches us Grammar.

A. We are taught Grammar by him. B. We are being taught Grammar by him. C. Grammar is taught to us by him. D. Grammar is being taught us by him.

Answer: Option A
Joining Sentences
7. Walk a bit faster. We will miss the bus. (A) If you don't walk a bit faster ..... (B) Either you walk a bit faster or ..... (C) Unless you walk a bit faster .....

A. Only A B. A and B C. Only C D. B and C E. A and C

Answer: Option E
Explanation: The two sentences are related to a condition (i.e) 'if you walk fast you will catch the bus. Hence, conjunctions like, if and 'unless' can be used to combine the two sentences effectively. 'Either ... or' is used to show a choice between two things which you would opt for. Here it is a condition where it is essential to walk faster if they have to catch the bus and not a choice.
8. They are making such a lot of noise. It is impossible to work. (A) As they are making such a ..... (B) Since they are making such a ..... (C) If they are making such a .....

A. Only A B. A and B C. Only B D. B and C E. All the three

Answer: Option B
Explanation: The two sentences are linked with a cause and its reason. The use of 'as', 'since' and 'because' can combine the sentences meaningfully. The use of 'if' is incorrect as it denotes a condition in the future.
9. He was a prolific writer. He was an eloquent speaker. (A) He was not only a prolific writer but also ..... (B) Besides being a prolific writer ..... (C) Since he was a prolific writer .....

A. Only B B. A and B C. Only A D. B and C E. All the three

Answer: Option B
Explanation: Apart from being a prolific writer, he was an eloquent speaker. This meaning is brought out using A and B as the probable starters.
Spotting Errors
10. These display (a) / the (b) / remarkable variety (c) / No error (d)

A. these display B. the C. remarkable variety D. no error

Answer: Option B
11. Most people would have (a) / attended the union meeting (b) / if they had (c) / had longer notice of it (d) / No error(e)

A. most people would have B. attended the union meeting C. if they had D. had longer notice of it E. no error

Answer: Option E
12. As soon as the teacher entered (a) / everyone fell (b) / in a silence (c) / No error (d)

A. as soon as the teacher entered B. everyone fell C. in a silence D. no error

Answer: Option C
Synonyms
13. Loquacious

A. Talkative B. Thirsty C. Beautiful D. Complicated

Answer: Option A
Explanation: loquacious means excessively talkative, or garrulous
14. Appall

A. Delirious B. Covered C. Dismay D. Confuse

Answer: Option C
Explanation: to appall is to overcome with shock, or to the dismay
15. Simulate

A. Excite B. Imitate C. Trick D. Apelike

Answer: Option B
Explanation: To simulate is to assume the outward appearance of, or to imitate
Sentence Improvement
16. My copy is as good or better than yours.

A. as good as or B. as good as C. as good and better D. none

Answer: Option B
17. She is worried about his health and also me.

A. also is me B. I also are C. so am I D. so come too

Answer: Option C
18. Do how I say.

A. as B. that C. like D. which

Answer: Option A
Error Correction (Phrase in colour)
19. You would not drive so fast; we have plenty of time.

A. will not B. had not C. need not D. do not E. No correction required

Answer: Option C
Explanation: The sentence suggests that driving fast is not necessary. Hence the most appropriate modal verb to suit this context would be 'need not'. 'Will not' suggests a simple future which is inapt. 'Had not' and 'do not' are illogical.
20. To be overweighed is not the same as being obese.

A. Being overweighed B. To be overweight C. Being overweight D. Being overweight E. No correction required

Answer: Option D
Explanation: The comparison is between 'being overweight' and 'being obese'. As the second part of the sentence has 'being obese' parallelism demands that the first part also takes the same be-form. Hence, 'being overweight' is the correct way of expressing the idea.
21. Scientists have estimated that millions of creatures living in water had been dying every year if they become entangled in plastic pollution or ingest it.

A. every year is dying as B. has died every year as if C. die every year when D. was dying every year when E. No correction required

Answer: Option C
Explanation: Scientists say that it happens 'every year'. Hence it is most apt to use the simple present tense (die) in this context. Also the use of 'if' as the conjunction is illogical. They die 'when they become entangled in'.
Para Completion
22. Stress is an inevitable part of sports. ---- Absence of stress leads to apathy and a disinterested performance. (A) Stress can be treated as a positive sign as well. (B) Stress is not necessarily bad: it is, after all, the body's way of rising to a challenge. (C) During stress, the mind becomes alert, the muscles tense as if ready for a fight or flight and the heart, lungs, and metabolism gets ready to act.

A. Only A B. Only B C. Only C D. A and B E. All the three

Answer: Option C
Explanation: The first statement states that stress cannot be avoided in sports. Statement C follows the first statement by elaborating on how stress is beneficial to the human body. The last sentence summarizes the paragraph by saying what the absence of stress would lead to. Thus only statement C forms a coherent paragraph with the two given statements.
23. If you are a doctor, one of the greatest honors to which you can aspire is to have a nightmarish disease named after you. ---- Eponyms bring color, tradition, and culture to medicine and also provide a useful shorthand. (A) Hundreds of so-called eponyms dot the medical textbooks, enshrining the name of a man or a woman who became the first to identify some horrible ailment, describe symptoms or devise a new diagnostic test. (B) But the time-honored practice is under threat, judging by a fierce debate in the August 2007 issue of the British Medical Journal. (C) Names, especially when it comes to obscure conditions or procedures, can cause confusion and are often historically untruthful, argue some of the anti-eponymists.

A. A and B B. Only A C. B and C D. Only C E. A and C

Answer: Option B
Explanation: Sentence A follows the first sentence as it tells us what this practice of naming a disease after a person is called (i.e.) eponym. And the last sentence highlights on the importance of using such eponyms. Hence the given two sentences along with sentence A forms a logical paragraph. Sentences B and C express the idea of the anti-eponymists and their debate with the pro-eponymists which is not necessary in this context.
24. Chronic pain is common among older people. ---- A new study has revealed that mind-body therapies such as yoga and meditation that cause interaction between the mind, body, and behavior can help the elderly get rid of chronic pain. (A) The people suffering from chronic pain can help themselves with some mind-body therapies which include yoga, meditation, progressive muscle relaxation, and tai chi. (B) Sufferers are often unable to receive adequate treatment because of limited physician training in pain management for the elderly and the increased likelihood of side effects from pain medication. (C) The mind-body therapies are well suited even to the frail older adults because of their gentle approach.

A. Only A B. Only B C. Only C D. A and B E. B and C

Answer: Option B
Explanation: The opening sentence talks about the relation between old age and chronic pain. Though without any other sentence the last sentence can follow the first to complete the idea, it is better to introduce sentence B in between as it gives a reason as to why the elderly people go in for mind-body therapies instead of another kind of treatment.
Sentence Completion
25. Amie agrees with the ______ that the grass is always greener on the other side of the fence.

A. perpetuity B. penchant C. maxim D. conformation E. fortitude

Answer: Option C
Explanation: Maxim (n.) is an established principle or a general truth, often a condensed version of practical truth.
26. The accused ----------- having made any statement.

A. refused B. rejected C. declaimed D. denied

Answer: Option D
27. It was ______ to think that it could possibly snow in the middle of the desert.

A. advantageous B. philosophical C. eroding D. preventative E. preposterous

Answer: Option E
Explanation: Preposterous (adj.) means contrary to common sense or utterly absurd.
Fill in the blanks
28. The police were forced to open tear gas shells on the _____ mob. (A) obdurate (B) docile (C) recalcitrant (D) steadfast (E) dogged (F) languid

A. A and E B. C and E C. A and C D. B and C E. E and F

Answer: Option C
Explanation: A mob can only be 'recalcitrant' (disobedient) or 'obdurate'. The word 'dogged' has a positive connotation and hence is not used with 'mob'.
29. After a protracted illness which left her weak and _____, she is now on the road to recovery. (A) energized (B) debilitated (C) invigorated (D) emaciated (E) robust (F) enervated

A. A and C B. B and F C. D and E D. B and D E. E and F

Answer: Option B
Explanation: A, C and E are ruled out because an illness, does not leave anyone 'energized', 'invigorated' or 'robust' (strong). D is inappropriate because a minor ailment does not leave a person 'emaciated' (thin). B and F are most appropriate.
Error Correction (Underlined Part)
30. I shall not detain you longer than it is a necessity.

A. it is a need B. it shall be needed C. it is necessary D. it will be a necessity E. No correction required

Answer: Option C
Explanation: The use of the noun 'necessity', is wrong. It should be used in the adjective form (i.e) necessary.
31. He went to his native village taking two day's leave.

A. two day's leave B. two day leaves C. two days to leave D. two leave days E. No correction required

Answer: Option A
Explanation: He has taken 'leave for two days'. Hence it becomes 'two days' 'leave' where's after the apostrophe need not be used.
Passage Completion
32. Choose the best word in place of ( III ) from the given passage

A. weakens B. initiates C. awakens D. strengthens E. volatile

Answer: Option A
33. Choose the best word in place of ( III ) from the given passage

A. weakens B. initiates C. awakens D. strengthens E. volatile

Answer: Option A
Substitution
34. One who walks in one’s sleep.

A. ignorant B. nematic C. dreamer D. somnambulist

Answer: Option D
3. A commonplace remark.

A. epigram B. remark C. statement D. statement

Answer: Option D
Idioms and Phrases
35. To cross swords with someone

A. to nurture vengeance against someone B. to make secret plans to harm someone C. to end a long-standing enmity with someone D. to have a verbal contest with someone E. to make an impression on someone

Answer: Option D
Explanation: 'To cross swords with someone' means to have a verbal contest with someone.
36. To shed crocodile tears

A. to pretend to be sad about something B. to have a difficult problem that makes one worried C. a sad thing that appears suddenly D. to feel worried anticipating some trouble E. to complain that someone else has done something wrong to one.

Answer: Option A
Explanation: When a person sheds 'crocodile tears' it means that he is pretending to be sad.
Antonyms
37.SOLDER

A. merge B. separate C. know D. ignore E. discard

Answer: Option B
Explanation: Solder means to join together, hence separate is its antonym.
38. SOGGY

A. juicy B. damp C. withered D. weak E. dry

Answer: Option E
Explanation: Soggy means very wet and soft, dry is its antonym.
Sentence Arrangement
39. The house (P) about half a mile distant (Q) that stands in front of us (R) was built of stones (S) which were dug out of its own site

A. QSPR B. QRPS C. QPRS D. QRSP

Answer: Option C
40. They are plant eaters (P) and various kinds of vegetation (Q) browsing on grass (R) and consume (S) vast quantities of pasture

A. RSQP B. QSRP C. QPRS D. RSPQ

Answer: Option C

1. In a code language if POSE is coded as OQNPRTDF, then the word TYPE will be coded as

A. SUXZOQFD B. SUXZQOFD C. SUXZOQDF D. SUXZQODE

Answer: Option A
Explanation: The word has been coded in such as way that codes for letter P are OQ (One letter behind and one letter ahead of P in alphabet). Similarly, codes for O are NP and so on.
2. In a certain code, BOXER is written as AQWGQ. How to VISIT is written in that code?

A. UKRKU B. UKRKS C. WKRKU D. WKRKS

Answer: Option B
Explanation: Letters at the odd places have been written one letter back, and letters at the even places have been written two letters ahead in the coded word as their positions in the alphabet.
3. If CLOTHES is EXHAUST and THRICE is STABLE, then SHIRT is

A. BLUSH B. STAUL C. THULE D. BLASH

Answer: Option D
Explanation: Using the above coding procedure as in the previous question, we find that the codes for letters $ and I will be B and L, and thus coding for SHIRT will be BLASH.
4. 3, 5, 11, 14, 17, 21

A. 21 B. 21 C. 14 D. 3

Answer: Option C
Explanation: Each of the numbers except 14 is an odd number. The number '14' is the only EVEN number.
5. 8, 27, 64, 100, 125, 216, 343

A. 27 B. 100 C. 125 D. 343

Answer: Option B
Explanation: The pattern is [latex]{2}^{3}[/latex], [latex]{3}^{3}[/latex], [latex]{4}^{3}[/latex], [latex]{5}^{3}[/latex], [latex]{6}^{3}[/latex], [latex]{7}^{3}[/latex]. But, 100 is not a perfect cube.
6. 10, 25, 45, 54, 60, 75, 80

A 10 B. 45 C. 54 D.75

Answer: Option c
Explanation: Each of the numbers except 54 is multiple of 5.
7. 396, 462, 572, 427, 671, 264

A. 396 B. 427 C. 671 D. 264

Answer: Option B
Explanation: In each number except 427, the middle digit is the sum of other two.
8. 6, 9, 15, 21, 24, 28, 30

A. 28 B. 21 C. 24 D. 30

Answer: Option A
Explanation: Each of the numbers except 28, is a multiple of 3.
9. 1, 4, 9, 16, 23, 25, 36

A. 9 B. 23 C. 35 D. 36

Answer: Option B
Explanation: Each of the numbers except 23, is perfect square.
10. 1, 4, 9, 16, 20, 36, 49

A. 1 B. 9 C. 20 D. 49

Answer: Option C
Explanation: The pattern is [latex]{1}^{2}[/latex], [latex]{2}^{2}[/latex], [latex]{3}^{2}[/latex], [latex]{4}^{2}[/latex], [latex]{5}^{2}[/latex], [latex]{6}^{2}[/latex], [latex]{7}^{2}[/latex]. But, instead of [latex]{5}^{2}[/latex], it is 20 which to be turned out. Directions: In each of the following questions two statements are given and these statements are followed by two conclusions numbered (1) and (2). You have to take the given two statements to be true even if they seem to be at variance from commonly known facts. Read the conclusions and then decide which of the given conclusions logically follows from the two given statements, disregarding commonly known facts. Give answer: (A) If only (1) conclusion follows (B) If only (2) conclusion follows (C) If either (1) or (2) follows (D) If neither (1) nor (2) follows and (E) If both (1) and (2) follow.
11. Statements: Some actors are singers. All the singers are dancers. Conclusions: Some actors are dancers. No singer is actor.

A. Only (1) conclusion follows B. Only (2) conclusion follows C. Either (1) or (2) follows D. Neither (1) nor (2) follows

Answer: Option A
Explanation:
12. Statements: All the harmoniums are instruments. All the instruments are flutes. Conclusions: All the flutes are instruments. All the harmoniums are flutes.

A. Only (1) conclusion follows B. Only (2) conclusion follows C. Either (1) or (2) follows D. Neither (1) nor (2) follows

Answer: Option B
Explanation:
13. Statements: Some mangoes are yellow. Some tixo are mangoes. Conclusions: Some mangoes are green. Tixo is a yellow.

A. Only (1) conclusion follows B. Only (2) conclusion follows C. Either (1) or (2) follows D. Neither (1) nor (2) follows

Answer: Option D
Explanation:
14. Statements: Some ants are parrots. All the parrots are apples. Conclusions: All the apples are parrots. Some ants are apples.

A. Only (1) conclusion follows B. Only (2) conclusion follows C. Either (1) or (2) follows D. Neither (1) nor (2) follows

Answer: Option B
Explanation:
15. Statements: Some papers are pens. All pencils are pens. Conclusions: Some pens are pencils. Some pens are papers.

A. Only (1) conclusion follows B. Only (2) conclusion follows C. Either (1) or (2) follows D. Both (1) and (2) follow

Answer: Option d
Explanation:
16. Statements: All the actors are girls. All the girls are beautiful. Conclusions: All the actors are beautiful. Some girls are actors.

A. Only (1) conclusion follows B. Only (2) conclusion follows C. Either (1) or (2) follows D. Both (1) and (2) follow

Answer: Option D
17: Statements: All the windows are doors. No door is a wall. Conclusions: Some windows are walls. No wall is a door.

A. Only (1) conclusion follows B. Only (2) conclusion follows C. Either (1) or (2) follows D. Both (1) and (2) follow

Answer: Option B
18. If + means /, * means -, / means * and - means +, then 8 + 6 * 4 / 3 - 4 = ?

A. -12 B. -20 / 3 C. 12 D. 20 / 3 E. None of these

Answer: Option B
Explanation: Using the correct symbols, we have: Given expression = 8 / 6 - 4 * 3 + 4 = 4 / 3 - 4 * 3 + 4 = 4 / 3 - 12 + 4 = - 20 / 3
19. If * means -, + means /, - means * and , means +, then 15 - 2 / 900 + 90 * 100 = ?

A. 190 B. 180 C. 90 D. 0 E. None of these

Answer: Option E
Explanation: Using the correct symbols, we have: Given expression = 15 * 2 + 900 / 90 - 100 = 15 * 2 + 10 - 100 = 30 + 10 - 100 = - 60
20. If + means /, - means *, / means -, * means +, what will be the value of 8 + 6 / 4 - 7 * 3 ?

A. - 71 / 3 B. - 23 / 2 C. 12 D. 14 E. None of these

Answer: Option A
Explanation: Using the correct symbols, we have: Given expression = 8 / 6 - 4 * 7 + 3 = (4 / 3) - 4 * 7 + 3 = (4 / 3) - 28 + 3 = - 71 / 3.
21. Sword : Slaughter :: Scalpel : ?

A. Murder B. Stab C. Surgery D. Chopping

Answer: Option C
Explanation: Second denotes the purpose for which the first is used.
22. Life: Autobiography:: Witness:?

A. Papers B. Truth C. Documents D. Acceptance

Answer: Option C
Explanation: Second contains an account of the first.
23. Chef : Restaurant :: Druggist : ?

A. Medicine B. Pharmacy C. Store D. Chemist

Answer: Option B
Explanation: Second is the working place of the first.
24. 3, 12, 8, 19, 13, 32, 18, 42, 23, 52

A. 12 B. 19 C. 42 D. 32 E. None of the above

Answer: Option B
Explanation: The sequence is a combination of the following two series: I. 3, 8, 13, 18, 23 and II. 12, 19, 32, 42, 52 The pattern in I has a constant difference of +5, and the pattern in II has a constant difference of +10. So, in II, 19 is wrong and should be replaced by (12+10) i.e. 22
25. 31, 2, 41, 3, 52, 4, 61, 5, 71, 6

A. 41 B. 61 C. 52 D. 31 E. 6

Answer: Option C
Explanation: The sequence is a combination of two given series: I. 31, 41, 52, 61, 71 and II. 2, 3, 4, 5, 6 So, the pattern in I is + 10 Thus, 52 is wrong and should be replaced by (41 + 10) i.e. 51.
26. Inventory is also referred to as:

A. stock B. warehouse capacity C. materials D. materials in hand

Answer: Option A
27. Critical path of the PERT chart is:

A. path which takes the longest time to complete the project B. the shortest path C. both of the above D. path which takes the shortest time to complete the project 6

Answer: Option A
28. A lockbox service is used for

A. depositing cash when bank is closed B. paying bank customer bills automatically C. storing papers in a bank vault D. depositing payments to bank customers

Answer: Option D
29. Controls of data communication deal with

A. the communication channel B. the computer C. terminals D. All of the above

Answer: Option D
30. Windows Naming Service (WINS)

A. dynamically allocates IP addresses to client computers B. runs on Windows NT W/S C. resolves computer names to IP addresses D. Increases broadcast traffic

Answer: Option C
31. How do you configure a printing pool?

A. Associate one print device with multiple printers B. Associate multiple print devices with one printer C. Associate multiple print devices with multiple printers D. Associate one physical print gear port with multiple printers

Answer: Option B
32. In which addressing mode the effective address of the operand is the contents of a register specified in the instruction and after accessing the operand, the contents of this register is incremented to point to the next item in the list?

A. index addressing B. indirect addressing C. auto increment D. auto decrement

Answer: Option C
33. Which of the following are(is) Language Processor(s)

A. assembles B. compilers C. interpreters D. All of the above

Answer: Option D
34. Fragmentation of the file system

A. occurs only if the file system is used improperly B. can always be prevented C. can be temporarily removed by compaction D. is a characteristic of all file systems

Answer: Option C
35. In virtual memory systems, Dynamic address translation

A. is the hardware necessary to implement paging B. stores pages at a specific location on disk C. is useless when swapping is used D. is part of the operating system paging algorithm

Answer: Option A
36. Which command is used to remove the read permission of the file 'note' from both the group and others?

A. chmod go+r note B. chmod go+rw note C. chmod go-x note D. chmod go-r note

Answer: Option D
37. Which command sends the word count of the file in file to the new file.

A. wc infile >newfile B. wc infile >newfile C. wc infile - newfile D. wc infile | newfile

Answer: Option A
38. Which command is used to extract specific columns from the file?

A. cat B. cut C. grep D. paste E. 6

Answer: Option B
39. Which command is used to remove a directory?

A. rd B. rmdir C. dldir D. rdir

Answer: Option B
40. Which of the following keys is used to replace a single character with a new text?

A. S B. s C. r D. c

Answer: Option B
41. Which command is used to sort the lines of data in a file in reverse order

A. sort B. sh C. st D. sort -r

Answer: Option D
42. ASCII and EBCDIC differ in

A. their efficiency in storing data B. the random and sequential access method C. the number of bytes used to store characters D. their collecting sequences

Answer: Option D
43. In which code the successive code characters differ in only one-bit position?

A. gray code B. excess 3 code C. 8421 code D. algebraic code

Answer: Option A
44. A positive AND gate is also a negative

A. NAND gate B. NOR gate C. AND gate D. OR gate

Answer: Option D
45. Address 200H contains the byte 3FH. What is the decimal equivalent of 3FH

A. 63 B. 32 C. 16 D. 38

Answer: Option A
46. An OR gate can be imagined as

A. switches connected in series B. switches connected in parallel C. MOS transistors connected in series D. All of the above

Answer: Option B
47. In which addressing mode, the effective address of the operand is generated by adding a constant value to the contents of register?

A. absolute mode B. indirect mode C. immediate mode D. index mode

Answer: Option D
48. A self-relocating program is one which

A. cannot be made to execute in any area of storage other than the one designated for it at the time of its coding or translation B. consists of a program and relevant information for its relocation C. can itself perform the relocation of its address-sensitive portions D. All of the above

Answer: Option C
49. Convert the 11014B machine language instructions into assembly language, assuming that they were not generated by pseudo-ops:

A. ASRA B. LOADA h#OD4E, i C. STOREA h#014B, d D. ADDA h#01FE, i

Answer: Option C
50. Which of the following functions is/ are performed by the loader?

A. Allocate space in memory for the programs and resolve symbolic references between object decks B. Physically place the machine instructions and data into memory C. Adjust all address dependent locations, such as address constants, to correspond to the allocated space D. All of the above

Answer: Option D

1. A man took a loan from a bank at the rate of 12% p.a. simple interest. After 3 years he had to pay Rs. 5400 interest only for the period. The principal amount borrowed by him was:

A. Rs. 2000 B. Rs. 10,000 C. Rs. 15,000 D. Rs. 20,000

Answer: Option (C)
Explanation: Principal = Rs. ([latex]\frac{100 \times 5400}{12 \times 3}[/latex])= Rs. 15000.
2. Due to the sun, a 6ft man casts a shadow of 4ft, whereas a pole next to the man casts a shadow of 36ft. What is the height of the pole?

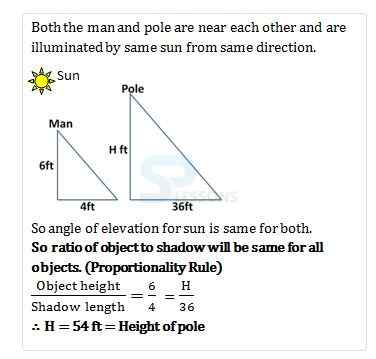
A. 63 ft B. 72 ft C. 54 ft D. 48 ft

Answer: Option (C)
Explanation:

3. A metallic sheet is of rectangular shape with dimensions 48 m x 36 m. From each of its corners, a square is cut off so as to make an open box. If the length of the square is 8 m, the volume of the box (in m3) is:

A. 4830 B. 5120 C. 6420 D. 8960

Answer: Option (B)
Explanation: Clearly, l = (48 - 16)m = 32 m, b = (36 -16)m = 20 m, h = 8 m. Volume of the box = (32 x 20 x 8) [latex]{m}^{3}[/latex] = 5120 [latex]{m}^{3}[/latex].
4. If log 2 = 0.30103, the number of digits in 264 is:

A. 18 B. 19 C. 20 D. 21

Answer: Option C
Explanation: log (264) = 64 x log 2 = (64 x 0.30103) = 19.26592 Its characteristic is 19. Hence, then a number of digits in 264 is 20.
5. X, Y, and Z are the three contestants in one km race. If X can give Y a start of 52 meters and X can also give Z a start of 83 meters, how many meters start Y can give Z?

A. 33.3 m B. 33 m C. 32 m D. 32.7 m

Answer: Option D
Explanation : While X runs 1000 metre, Y runs (1000-52)=948 metre and Z runs (1000-83)=917 metre i.e., when Y runs 948 meters, Z runs 917 meters When Y runs 1000 metre, Z runs ([latex]\frac{917}{948}[/latex])×1000 = 967.30 metre i.e., Y can give Z (1000-967.30) = 32.7 meters.
6. 6156 ÷ √? × 53 = 4028

A. 6889 B. 6241 C. 5929 D. 6561 None of these

Answer: D
Solution: ([latex]\frac{6153 \times 53}{\sqrt{?}}[/latex]) = 4028 ? = 80.96 ≈ 81 ? = 6561.
7. If a person walks at 14 km/hr instead of 10 km/hr, he would have walked 20 km more. The actual distance traveled by him is:

A. 50 km B. 56 km C. 70 km D. 80 km

Answer: Option A
Explanation: Let the actual distance traveled be x km. Then,([latex]\frac{x}{10}[/latex]) = ([latex]\frac{x + 20}{14}[/latex]) 14x = 10x + 200 4x = 200 x = 50 km.
8. In a camp, there is a meal for 120 men or 200 children. If 150 children have taken the meal, how many men will be catered to with remaining meal?

A. 20 B. 30 C. 40 D. 50

Answer: Option B
Explanation: There is a meal for 200 children. 150 children have taken the meal. The remaining meal is to be catered to 50 children. Now, 200 children 120 men. 50 children =([latex]\frac{120}{200}[/latex]) x 50 = 30 men.
9. In how many different ways can the letters of the word 'DETAIL' be arranged in such a way that the vowels occupy only the odd positions?

A. 32 B. 48 C. 36 D. 60 E. 120

Answer: Option C
Explanation: There are 6 letters in the given word, out of which there are 3 vowels and 3 consonants. Let us mark these positions as under: (1) (2) (3) (4) (5) (6) Now, 3 vowels can be placed at any of the three places out 4, marked 1, 3, 5. Number of ways of arranging the vowels = 3P3 = 3! = 6. Also, the 3 consonants can be arranged at the remaining 3 positions. Number of ways of these arrangements = 3P3 = 3! = 6. Total number of ways = (6 x 6) = 36.
10. (256)0.16 x (256)0.09 = ?

A. 4 B. 16 C. 64 D. 256.25

Answer: Option A
Explanation: (256)0.16 x (256)0.09 = (256)(0.16 + 0.09) = (256)0.25 = (256)(25/100) = (256)(1/4) = (44)(1/4) = 44(1/4) = 41 = 4
11. A tank is filled in 5 hours by three pipes A, B and C. The pipe C is twice as fast as B and B is twice as fast as A. How much time will pipe A alone take to fill the tank?

A. 20 hours B. 25 hours C. 35 hours D. Cannot be determined E. None of these

Answer: Option C
Explanation: Suppose pipe A alone takes x hours to fill the tank. Then, pipes B and C will take ([latex]\frac{x}{2}[/latex]) and ([latex]\frac{x}{4}[/latex]) hours respectively to fill the tank. ([latex]\frac{1}{x}[/latex]) + ([latex]\frac{2}{x}[/latex]) + ([latex]\frac{4}{x}[/latex]) =([latex]\frac{1}{5}[/latex]) 1 ([latex]\frac{7}{x}[/latex]) = ([latex]\frac{1}{5}[/latex]) x = 35 hrs.
13. The speed of a boat in still water in 15 km/hr and the rate of current is 3 km/hr. The distance traveled downstream in 12 minutes is:

A. 1.2 km B. 1.8 km C. 2.4 km D. 3.6 km

Answer: Option D
Explanation: Speed downstream = (15 + 3) kmph = 18 kmph. Distance travelled = 18 x ([latex]\frac{12}{60}[/latex])km = 3.6 km.
14. On dividing a number by 357, we get 39 as the remainder. On dividing the same number 17, what will be the remainder?

A. 0 B. 3 C. 5 D. 11

Answer: Option C
Explanation: Let x be the number and y be the quotient. Then, x = 357 x y + 39 = (17 x 21 x y) + (17 x 2) + 5 = 17 x (21y + 2) + 5) Required remainder = 5.
15. A began a business with Rs. 85,000. He was joined afterward by B with Rs. 42,500. For how much period does B join, if the profits at the end of the year are divided in the ratio of 3: 1?

A. 4 months B. 5 months C. 6 months D. 8 months

Answer: Option D
Explanation: Suppose B joined for x months. Then, Then, ([latex]\frac{1800\times 12}{42500\times x}[/latex])=([latex]\frac{3}{1}[/latex]) x = ([latex]\frac{1800\times 12}{42500\times 3}[/latex]) = 8. So, B joined for 8 months.
16. The fourth proportional to 5, 8, 15 is:

A. 18 B. 24 C. 19 D. 20

Answer: Option B
Explanation: Let the fourth proportional to 5, 8, 15 be x. Then, 5: 8: 15: x 5x = (8 x 15) x = ([latex]\frac{(8 x 15)}{5}[/latex]) = 24.
17. Find the lowest common multiple of 24, 36 and 40.

A. 120 B. 240 C. 360 D. 480

Answer: Option C
Explanation: 2 | 24 - 36 - 40 -------------------- 2 | 12 - 18 - 20 -------------------- 2 | 6 - 9 - 10 ------------------- 3 | 3 - 9 - 5 ------------------- | 1 - 3 - 5 L.C.M. = 2 x 2 x 2 x 3 x 3 x 5 = 360.
18. The true discount on a bill of Rs. 540 is Rs. 90. The banker's discount is:

A. Rs. 60 B. Rs. 108 C. Rs. 110 D. Rs. 112

Answer: Option B
Explanation: P.W. = Rs. (540 - 90) = Rs. 450. S.I. on Rs. 450 = Rs. 90. S.I. on Rs. 540 = Rs. ([latex]\frac{90}{450}[/latex]) x 540 = Rs. 108. B.D. = Rs. 108. Compound Interest [latex]1600 \times (1 + \frac{5}{2 \times100})^{2}[/latex]
19. The effective annual rate of interest corresponding to a nominal rate of 6% per annum payable half-yearly is:

A. 6.06% B. 6.07% C. 6.08% D. 6.09%

Answer: Option D
Explanation: Amount of Rs. 100 for 1 year when compounded half-yearly = Rs. [latex]100 \times (1 + \frac{3}{100})^{2} [/latex] Effective rate = (106.09 - 100)% = 6.09%
20. A rectangular field has to be fenced on three sides leaving a side of 20 feet uncovered. If the area of the field is 680 sq. feet, how many feet of fencing will be required?

A. 95 B. 92 C. 88 D. 82

Answer: Option C
Explanation: Area of the field = 680 sq. feet. Length of the adjacent sides are 20 feet and ([latex]\frac{680}{20}[/latex]) = 34 feet. Required length of the fencing = 20 + 34+ 34 = 88 feet
21. A can do a piece of work in 4 hours; B and C together can do it in 3 hours, while A and C together can do it in 2 hours. How long will B alone take to do it?

A. 8 hours B. 10 hours C. 12 hours D. 24 hours

Answer: Option C
Explanation: A's 1 hour's work = ([latex]\frac{1}{4}[/latex]) (B + C)'s 1 hour's work = ([latex]\frac{1}{3}[/latex]) (A + C)'s 1 hour's work = ([latex]\frac{1}{2}[/latex]) (A + B + C)'s 1 hour's work = ([latex]\frac{1}{4}[/latex] + [latex]\frac{1}{3}[/latex]) = ([latex]\frac{7}{12}[/latex]) B's 1 hour's work = ([latex]\frac{7}{12}[/latex] - [latex]\frac{1}{2}[/latex]) = ([latex]\frac{1}{12}[/latex]) Therefore B alone will take 12 hours to do the work.
22. Find the ratio in which rice at Rs. 7.20 a kg be mixed with rice at Rs. 5.70 a kg to produce a mixture worth Rs. 6.30 a kg.

A. 1: 3 B. 2: 3 C. 3: 4 D. 4: 5

Answer: Option B
Explanation: By the rule of allegation:

Required ratio = 60 : 90 = 2 : 3.
23. 617 + 6.017 + 0.617 + 6.0017 = ?

A. 6.2963 B. 62.965 C. 629.6357 D. None of these

Answer: Option C
Explanation: 617.00 6.017 0.617 + 6.0017 -------- 629.6357 ---------
24. In a lottery, there are 10 prizes and 25 blanks. A lottery is drawn at random. What is the probability of getting a prize?

A. [latex]\frac{1}{10}[/latex] B. [latex]\frac{2}{5}[/latex] C. [latex]\frac{2}{7}[/latex] D. [latex]\frac{5}{7}[/latex]

Answer: Option C
Explanation: P (getting a prize) = [latex]\frac{10}{10 + 25}[/latex] = [latex]\frac{10}{35}[/latex] = [latex]\frac{2}{7}[/latex].
25. The average monthly income of P and Q is Rs. 5050. The average monthly income of Q and R is Rs. 6250 and the average monthly income of P and R are Rs. 5200. The monthly income of P is:

A. 3500 B. 4000 C. 4050 D. 5000

Answer: Option B
Explanation: Let P, Q and R represent their respective monthly incomes. Then, we have: P + Q = (5050 x 2) = 10100 .... (i) Q + R = (6250 x 2) = 12500 .... (ii) P + R = (5200 x 2) = 10400 .... (iii) Adding (i), (ii) and (iii), we get: 2(P + Q + R) = 33000 or P + Q + R = 16500 .... (iv) Subtracting (ii) from (iv), we get P = 4000. P's monthly income = Rs. 4000.
26. A man invested Rs. 1552 in stock at 97 to obtain an income of Rs. 128. The dividend from the stock is:

A. 7.5% B. 8% C. 9.7% D. None of these

Answer: Option B
Explanation: By investing Rs. 1552, income = Rs. 128. By investing Rs. 97, income = Rs. ([latex]\frac{128}{1552}[/latex] x 97 ) = Rs. 8. Dividend = 8%
3. The square root of 64009 is:

A. 253 B. 347 C. 363 D. 803

Answer: Option A
Explanation: 2|64009( 253 |4 |---------- 45|240 |225 |---------- 503| 1509 | 1509 |---------- | X |---------- [latex]\sqrt{64009}[/latex] = 253.
27. A man is 24 years older than his son. In two years, his age will be twice the age of his son. The present age of his son is:

A. 14 years B. 18 years C. 20 years D. 22 years

Answer: Option D
Explanation: Let the son's present age be x years. Then, man's present age = (x + 24) years. (x + 24) + 2 = 2(x + 2) x + 26 = 2x + 4 x = 22.
28. Sachin is younger than Rahul by 7 years. If their ages are in the respective ratio of 7 : 9, how old is Sachin?

A. 16 years B. 18 years C. 28 years D. 24.5 years E. None of these

Answer: Option D
Explanation: Let Rahul's age be x years. Then, Sachin's age = (x - 7) years. [latex]\frac {x - 7}{x}[/latex] = [latex]\frac {7}{9}[/latex] 9x - 63 = 7x 2x = 63 x = 31.5 Hence, Sachin's age =(x - 7) = 24.5 years.
29. The least perfect square, which is divisible by each of 21, 36 and 66 is:

A. 213444 B. 214344 C. 214434 D. 231444

Answer: Option A
Explanation: L.C.M. of 21, 36, 66 = 2772. Now, 2772 = 2 x 2 x 3 x 3 x 7 x 11 To make it a perfect square, it must be multiplied by 7 x 11. So, required number = 2[latex]^{2}[/latex] x 3[latex]^{2}[/latex] x 7[latex]^{2}[/latex] x 11[latex]^{2}[/latex]= 213444
30. The cost price of a Rs. 100 stock at 4 discount, when brokerage is[latex]\frac {1}{4}[/latex]% is:

A. Rs. 95.75 B. Rs. 96 C. Rs. 96.25 D. Rs. 104.25

Answer: Option C
Explanation: C.P. = Rs. (100 - 4 + [latex]\frac {1}{4}[/latex])= Rs. 96.25
31. In Arun's opinion, his weight is greater than 65 kg but less than 72 kg. His brother doest not agree with Arun and he thinks that Arun's weight is greater than 60 kg but less than 70 kg. His mother's view is that his weight cannot be greater than 68 kg. If all are them are correct in their estimation, what is the average of different probable weights of Arun?

A. 67 kg. B. 68 kg. C. 69 kg. D. Data inadequate E. None of these

Answer: Option A
Explanation: Let Arun's weight by X kg. According to Arun, 65 < X < 72 According to Arun's brother, 60 < X < 70. According to Arun's mother, X <= 68 The values satisfying all the above conditions are 66, 67 and 68. Required average = [latex]\frac {66 + 67 + 68}{3}[/latex] = [latex]\frac {201}{3}[/latex] = 67 kg.
32. One card is drawn at random from a pack of 52 cards. What is the probability that the card drawn is a face card (Jack, Queen and King only)?

A. [latex]\frac {1}{13}[/latex] B. [latex]\frac {3}{13}[/latex] C. [latex]\frac {1}{4}[/latex] D. [latex]\frac {9}{52}[/latex]

Answer: Option B
Explanation: Clearly, there are 52 cards, out of which there are 12 face cards. P (getting a face card) = [latex]\frac {12}{52}[/latex] = [latex]\frac {3}{13}[/latex].
33. Which of the following is equal to 3.14 x 10[latex]^{6}[/latex] ?

A. 314 B. 3140 C. 3140000 D. None of these

Answer: Option C
Explanation: 3.14 x 10[latex]^{6}[/latex] = 3.14 x 1000000 = 3140000.
34. 4 men and 6 women can complete a work in 8 days, while 3 men and 7 women can complete it in 10 days. In how many days will 10 women complete it?

A. 35 B. 40 C. 45 D. 50

Answer: Option B
Explanation: Let 1 man's 1 day's work = x and 1 woman's 1 day's work = y. Then, 4x + 6y = [latex]\frac {1}{8}[/latex] and 3x + 7y = [latex]\frac {1}{10}[/latex]. Solving the two equations, we get: x = [latex]\frac {11}{400}[/latex] , y = [latex]\frac {1}{400}[/latex] 1 woman's 1 day's work = [latex]\frac {1}{400}[/latex] . 10 women's 1 day's work = ([latex]\frac {1}{400}[/latex] x 10) = [latex]\frac {1}{40}[/latex] . Hence, 10 women will complete the work in = 40 days.
35. A boat having a length of 3 m and breadth 2 m is floating on a lake. The boat sinks by 1 cm when a man gets on it. The mass of the man is:

A. 12 kg B. 60 kg C. 72 kg D. 96 kg

Answer: Option B
Explanation: Volume of water displaced = (3 x 2 x 0.01) m[latex]^{3}[/latex] = 0.06 m[latex]^{3}[/latex]. Mass of man = Volume of water displaced x Density of water = (0.06 x 1000) kg = 60 kg.
36. The effective annual rate of interest corresponding to a nominal rate of 6% per annum payable half-yearly is:

A. 6.06% B. 6.07% C. 6.08% D. 6.09%

Answer: Option D
Explanation: Amount of Rs. 100 for 1 year when compounded half-yearly = Rs. (100 x (1 + [latex]\frac {3}{100})^{2}[/latex]) = Rs. 106.09 Effective rate = (106.09 - 100)% = 6.09%
37. The present worth of a certain bill due sometime hence is Rs. 800 and the true discount is Rs. 36. The banker's discount is:

A. Rs. 37 B. Rs. 37.62 C. Rs. 34.38 D. Rs. 38.98

Answer: Option B
Explanation: B.G. =[latex]\frac {(T.D.)^{2}}{P.W.}[/latex] = Rs.[latex]\frac {36 \times 36}{800}[/latex]= Rs. 1.62 B.D. = (T.D. + B.G.) = Rs. (36 + 1.62) = Rs. 37.62
38. The sum of the three numbers is 98. If the ratio of the first to second is 2 :3 and that of the second to the third is 5: 8, then the second number is:

A. 20 B. 30 C. 48 D. 58

Answer: Option B
Explanation: Let the three parts be A, B, C. Then, A : B = 2 : 3 and B : C = 5 : 8 = (5 x [latex]\frac {3}{5}[/latex]) : (8 x [latex]\frac {3}{5}[/latex]) = 3 : [latex]\frac {24}{5}[/latex] A : B : C = 2 : 3 : [latex]\frac {24}{5}[/latex] = 10 : 15 : 24 B = (98 x [latex]\frac {15}{49}[/latex]) = 30.
39. A began a business with Rs. 85,000. He was joined afterward by B with Rs. 42,500. For how much period does B join, if the profits at the end of the year are divided in the ratio of 3: 1?

A. 4 months B. 5 months C. 6 months D. 8 months

Answer: Option D
Explanation: Suppose B joined for x months. Then, Then, [latex]\frac {85000 \times 12 }{42500 \times x}[/latex] = [latex]\frac {3}{1}[/latex] x = [latex]\frac {85000 \times 12 }{42500 \times 3}[/latex] = 8. So, B joined for 8 months.
40. How many 3 digit numbers are divisible by 6 in all?

A. 149 B. 150 C. 151 D. 166

Answer: Option B
Explanation: Required numbers are 102, 108, 114, ... , 996 This is an A.P. in which a = 102, d = 6 and l = 996 Let the number of terms be n. Then, a + (n - 1)d = 996 102 + (n - 1) x 6 = 996 6 x (n - 1) = 894 (n - 1) = 149 n = 150.
41. A boatman goes 2 km against the current of the stream in 1 hour and goes 1 km along with the current in 10 minutes. How long will it take to go 5 km in stationary water?

A. 40 minutes B. 1 hour C. 1 hr 15 min D. 1 hr 30 min

Answer: Option C
Explanation: Rate downstream = [latex]\frac {1}{10}[/latex] x 60 km/hr = 6 km/hr. Rate upstream = 2 km/hr. Speed in still water = [latex]\frac {1}{2}[/latex] (6 + 2) km/hr = 4 km/hr. Required time = [latex]\frac {5}{4}[/latex]hrs = 1 [latex]\frac {1}{4}[/latex] hrs = 1 hr 15 min.
42. Two pipes A and B can fill a tank in 15 minutes and 20 minutes respectively. Both the pipes are opened together but after 4 minutes, pipe A is turned off. What is the total time required to fill the tank?

A. 10 min. 20 sec. B. 11 min. 45 sec. C. 12 min. 30 sec. D. 14 min. 40 sec.

Answer: Option D
Explanation: Part filled in 4 minutes = 4 ([latex]\frac {1}{15}[/latex] + [latex]\frac {1}{20}[/latex]) = [latex]\frac {7}{15}[/latex]. Remaining part = (1 - [latex]\frac {7}{15}[/latex]) = [latex]\frac {8}{15}[/latex]. Part filled by B in 1 minute = [latex]\frac {1}{20}[/latex] [latex]\frac {1}{20}[/latex] : [latex]\frac {8}{15}[/latex] :: 1 : x x = ([latex]\frac {8}{15} \times 1 \times 20[/latex]) = 10 [latex]\frac {2}{3}[/latex]min = 10 min. 40 sec. The tank will be full in (4 min. + 10 min. + 40 sec.) = 14 min. 40 sec.
43. (17)[latex]^{3.5}[/latex] x (17)[latex]^{?}[/latex] = 17[latex]^{8}[/latex]

A. 2.29 B. 2.75 C. 4.25 D. 4.5

Answer: Option D
Explanation: Let (17)[latex]^{3.5}[/latex] x (17)[latex]^{x}[/latex] = 17[latex]^{8}[/latex]x. Then, (17)[latex]^{3.5}[/latex] + x = 17[latex]^{8}[/latex]. 3.5 + x = 8 x = (8 - 3.5) x = 4.5
44. In how many different ways can the letters of the word 'MATHEMATICS' be arranged so that the vowels always come together?

A. 10080 B. 4989600 C. 120960 D. None of these

Answer: Option C
Explanation: In the word 'MATHEMATICS', we treat the vowels AEAI as one letter. Thus, we have MTHMTCS (AEAI). Now, we have to arrange 8 letters, out of which M occurs twice, T occurs twice and the rest are different. A number of ways of arranging these letters = [latex]\frac {8!}{(2!)(2!)}[/latex] = 10080. Now, AEAI has 4 letters in which A occurs 2 times and the rest are different. A number of ways of arranging these letters = [latex]\frac {4!}{2!}[/latex] = 12. Required number of words = (10080 x 12) = 120960.
45. In a camp, there is a meal for 120 men or 200 children. If 150 children have taken the meal, how many men will be catered to with remaining meal?

A. 20 B. 30 C. 40 D. 50

Answer: Option B
Explanation: There is a meal for 200 children. 150 children have taken the meal. The remaining meal is to be catered to 50 children. Now, 200 children = 120 men. 50 children = [latex]\frac {120}{200}[/latex] x 50 = 30 men.
46. A farmer traveled a distance of 61 km in 9 hours. He travelled partly on foot @ 4 km/hr and partly on bicycle @ 9 km/hr. The distance traveled on foot is:

A. 14 km B. 15 km C. 16 km D. 17 km

Answer: Option C
Explanation: Let the distance traveled on foot be x km. Then, distance travelled on bicycle = (61 -x) km. So, [latex]\frac {x}{4}[/latex] + [latex]\frac {(61 -x)}{9}[/latex] = 9 9x + 4(61 -x) = 9 x 36 5x = 80 x = 16 km.
47. A fires 5 shots to B's 3 but A kills only once in 3 shots while B kills once in 2 shots. When B has missed 27 times, A has killed:

A. 30 birds B. 60 birds C. 72 birds D. 90 birds

Answer: Option A
Explanation: Let the total number of shots be x. Then, Shots fired by A = [latex]\frac {5}{8}[/latex]x Shots fired by B = [latex]\frac {3}{8}[/latex]x Killing shots by A = [latex]\frac {1}{3}[/latex] of [latex]\frac {5}{8}[/latex] x = [latex]\frac {5}{24}[/latex]x Shots missed by B = [latex]\frac {1}{2}[/latex] of [latex]\frac {3}{8}[/latex] x = [latex]\frac {3}{16}[/latex]x [latex]\frac {3 \times x}{16}[/latex] = 27 or x = [latex]\frac {27 \times 16}{3}[/latex] = 144. Birds killed by A = [latex]\frac {5x}{24}[/latex] = [latex]\frac {5}{24}[/latex] x 144 = 30.
48. A can run 22.5 m while B runs 25 m. In a kilometer race, B beats A by:

A. 100 m B. 111[latex]\frac {1}{9}[/latex] m C. 25 m D. 50 m

Answer: Option A
Explanation: When B runs 25 m, A runs [latex]\frac {45}{2}[/latex] m. When B runs 1000 m, A runs ([latex]\frac {45}{2}[/latex] x [latex]\frac {1}{25}[/latex] x 1000) m = 900 m. B beats A by 100 m.
49. If log10 5 + log10 (5x + 1) = log10 (x + 5) + 1, then x is equal to:

A. 1 B. 3 C. 5 D. 10

Answer: Option B
Explanation: [latex]log_{10}[/latex] 5 + [latex]log_{10}[/latex] (5x + 1) = [latex]log_{10}[/latex] (x + 5) + 1 [latex]log_{10}[/latex] 5 + [latex]log_{10}[/latex] (5x + 1) = [latex]log_{10}[/latex] (x + 5) + [latex]log_{10}[/latex] 10 [latex]log_{10}[/latex] [5 (5x + 1)] = [latex]log_{10}[/latex] [10(x + 5)] 5(5x + 1) = 10(x + 5) 5x + 1 = 2x + 10 3x = 9 x = 3.
50. A hall is 15 m long and 12 m broad. If the sum of the areas of the floor and the ceiling is equal to the sum of the areas of four walls, the volume of the hall is:

A. 720 B. 900 C. 1200 D. 1800

Answer: Option C
Explanation: 2(15 + 12) x h = 2(15 x 12) h = [latex]\frac{180}{27}[/latex] m = [latex]\frac{20}{3}[/latex] m. Volume = ([latex]{15 \times 12 \times \frac {20}{3}}[/latex]) m[latex]^{3}[/latex] = 1200 m[latex]^{3}[/latex].